回归知识本质，提升解题能力

摘 要：解题过程是数学解题教学的关键环节，其不仅能深化学生对解析几何相关内容的理解，还能深化学生对知识本质的理解与掌握.

本文通过对高中数学解析几何问题解题策略的探究，促进学生数学学科核心素养的提高，提升其解决数学问题的能力.

关键词：高中数学；知识本质；解析几何；解题能力

解析几何主要是对几何问题进行研究，其解答方法主要是代数方法.解析几何中的知识本质就是通过代数方法进行几何问题求解.^［1］由于解析几何题有着较高的难度和较强的综合性，对学生的计算能力有着较高的要求，所以学生在解答几何问题时，常常存在解题思路混乱、方法选择不正确、计算错误等问题，这就需要学生回归几何知识的本质，立足多角度对几何问题进行探讨，以实现解题过程的优化，提高计算与解题能力.^［2］

1 高中数学解析几何的解题技巧探讨

1.1 与代数知识密切结合

经过大量的解析几何题的求解经验可知，在解析几何的问题解答中，利用坐标系，并按照代数方法进行几何问题的求解，是十分常见的一种方法.^［3］通常来说，直接进行解析几何题求解时，学生常常毫无头绪，运用代数方法则能有效求解相关几何问题.高中数学的解析几何主要是对点的轨迹形成的直线、圆以及圆锥曲线进行研究，都采取了坐标工具，即按照直线、圆以及圆锥曲线的具体定义或者图形特征，对其方程进行探究，对直线、圆以及圆锥曲线具备的几何性质加以研究，通常能充分呈现出坐标法解答解析几何题的重要性.^［4］

1.2 运用几何图形的性质，简化解题过程

在求解几何图形的有关问题时，可有效运用图形性质，把代数知识和几何知识有效结合，以实现解析几何问题的简化，并在考试过程中获得显著的优势.^［5］同时，如果采用的解题方法较为简单，解题的实际出错率就会明显减少.通过数形结合进行几何问题求解时，通常包含了四类问题，即轨迹求解、求值、求范围、证明问题.

例如，对曲线的轨迹方程进行求解的时候，可运用几何条件，对轨迹的曲线类型进行判断，并经过待定系数法解决解析几何问题.

1.3 运用函数变量解决问题

函数可呈现出客观世界当中变量之间的依赖关系，且在高中数学的课堂教学中占据着重要地位.在具体解题中，通过函数变量进行高效解题，通常能够使解题的整个过程变得更为简单.就解析几何题来说，点或者线产生改变，就造成图形当中其他的量发生改变，该类问题，则能通过函数变量加以求解.^［6］

2 高中数学解析几何问题解答策略

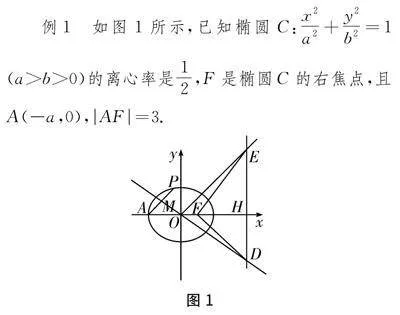
例1 如图1所示，已知椭圆C：x2a2+y2b2=1（a＞b＞0）的离心率是12，F是椭圆C的右焦点，且A（-a，0），|AF|=3.

（1）求椭圆C的方程.

（2）设O是原点，P是椭圆上一点，点P并非是椭圆长轴的端点，AP的中点是M，直线OM和直线x=4相交于点D，过O且与直线AP平行的直线与直线x=4相交于点E，求证：∠ODF=∠OEF.

分析：本题第（1）问相对简单，运用解析几何相关知识

就能求解.第（2）问主要是证明两个角是相等的，则需明确两个角为何相等，即P是椭圆上的点，AP的中

点M和原点O相连接，再加以延长，和直线x=4相交于点D，且点E是过O与直线AP平行的直线和直线x=4相交而得出的，从而获得线段DF与EF相等，得出∠ODF与∠OEF.

由此可知，两个角和点P有着密切关联，因此，本题可由直线AP的方程式与点P坐标作为切入点，进行解题.

解析：（1）依据椭圆的离心率是12，A（-a，0）以及|AF|=3，可得出椭圆C的方程为x24+y23=1.

第（2）题可通过多种方法进行求解.

解法1：由（1）可得点A的坐标为（-2，0），设直线AP的方程是y=k（x+2）（k≠0），将直线代入椭圆方程，整理可得

（4k2+3）x2+16k2x+16k2-12=0，明显有Δ＞0，设AP的中点为M（x0，y0），P（x1，y1），则-2+x1=-16k24k2+3，即x0=-2+x12=-8k24k2+3，y0=k（x0+2）=6k4k2+3，由此可知，点M的坐标为-8k24k2+3，6k4k2+3，直线OM的斜率为6k4k2+3-8k24k2+3=-34k，此时，可求得OM的直线方程为

y=-34kx，令x=4，可得点D4，-3k，设直线OE方程式为y=kx，令x=4，可得到点E坐标是（4，4k），由右焦点F（1，0）可得出直线EF的斜率为4k4-1=4k3，则EF⊥OM，记垂足为G.

又有直线DF的斜率为-3k4-1=-1k，即DF⊥OE，记垂足为K.

在Rt△EGO和Rt△DKO中，∠ODF和∠OEF都与∠EOD互余，所以∠ODF=∠OEF.

解法2：

由（1）可得点A的坐标为（-2，0），设P（x1，y1）（x1≠±2），其中3x21+4y21=12，由于直线AP的中点是M，可得M的坐标为x1-22，y12，则直线OM的斜率为kOM=y1x1-2，直线OM的方程是y=y1x1-2x，令x=4，可得

点D的坐标是4，4y1x1-2，由此可知直线OE的方程为y=y1x1+2x，

令x=4，可得点E的坐标是4，4y1x1+2.由右焦点F（1，0）可得直线EF的斜率为kEF=4y13（x1+2），由于kOM·kEF=y1x1-2·4y13（x1+2）=4y213（x21-4）=-1，则

EF⊥OM，同理得DF⊥OE，进而得证∠ODF=∠OEF.

解法3：

由（1）可得点A的坐标为（-2，0），设P（x1，y1）（x1≠±2），其中的3x21+4y21-12=0，由于直线AP的中点是M，可得M的坐标为x1-22，y12，则直线OM的斜率为kOM=y1x1-2，直线OM的方程是y=y1x1-2x，令x=4，可得到点D的坐标是4，4y1x1-2.设直线x=4和x轴相交于点H，设∠ODH=α，∠FDH=β，则有tanα=4｜yD｜，tanβ=3｜yD｜.

因此，tan∠ODF=tan（α-β）=｜yD｜y2D+12，同理求解出tan∠OEF=｜yE｜y2E+12，根据题意可知，yD、yE为异号，可设yE＞0，

则|yE|y2E+12-|yD|y2D+12=yEy2E+12+yDy2D+12=yE（y2D+12）+yD（y2E+12）（y2E+12）（y2D+12）.又有yE（y2D+12）+yD（y2E+12）=（yE+yD）（yEyD+12）=（yE+yD）4y1x1+24y1x1-2+12=（yE+yD）16y21x21-4+12.又有点P（x1，y1）位于椭圆上，则3x21+4y21-12=0，即（yE+yD）16y21x21-4+12=（yE+yD）·12（4-x21）x21-4+12=（yE+yD）（-12+12）=0，由此可知，tan∠ODF=tan∠OEF，根据题意可知∠ODF、∠OEF是锐角，则∠ODF=∠OEF.

例2 如图2所示，已知直线l：y=kx+2和椭圆C：x24+y2=1相交于不同的两点A、B.设直线OA、OB的斜率是k1、k2，且有k1=λk2，求实数λ的取值范围.

解析：联立直线l与椭圆C的方程，可得出k值的取值范围，设A、B两点坐标，通过两点的斜率公式得出k1、k2，构建其λ和k的代数关系式.

联立方程y=kx+2，

x24+y2=1，可得（4k2+1）x2+16kx+12=0，由Δ=4k2-3＞0，解得k²＞34，设A（x1，y1），B（x2，y2），则有x1+x2=-16k4k2+1，x1x2=124k2+1，由此可得

λ=k1k2=y1x1y2x2=kx1x2+2x2kx1x2+2x1=12k4k2+1+2x212k4k2+1+2x1①.由此可知，①式是本题解答的关键.

解法1：依据对称性可知，设k＞0，当x1＜x2时，可以得到x1=-8k-24k2-34k2+1，x2=-8k+24k2-34k2+1，将其代入

①式可知，λ=12k4k2+1+-16k+44k2-34k2+112k4k2+1+-16k-44k2-34k2+1=k-4k2-3k+4k2-3=1-4-3k21+4-3k2=-1+21+4-3k2.由于k2∈34，+∞，则4-3k2∈（0，2），由此可得λ∈-13，1.当x1＞x2的时候，有x1=-8k+24k2-34k2+1，x2=-8k-24k2-34k2+1②，如果k2=1，可得A点的坐标-65，45，B点坐标（-2，0），此时

k1=-23，k2=0，得λ∈；如果k2∈34，1∪（1，+∞），将②式代入①式，化简可得

λ=-1+21-4-3k2，由于k2∈34，1∪（1，+∞），则1-4-3k2∈（-1，0）∪（0，1），由此可得

λ∈（-∞，-3）∪（1，+∞）.

综上所述

λ∈（-∞，-3）∪-13，1∪（1，+∞）.

解法2：由于x1+x2=-16k4k2+1，x1x2=124k2+1，则

x1x2=-34k（x1+x2），将其代入①

式可得

λ=kx1x2+2x2kx1x2+2x1=-34（x1+x2）+2x2-34（x1+x2）+2x1=54x2-34x154x1-34x2=5x2-3x15x1-3x2=5-3x1x25x1x2-3.令t=x1x2，可知t＞0，

λ=5-3x1x25x1x2-3=5-3t5t-3=-35+165（5t-3）.

（x1+x2）2x1x2=x1x2+x2x1+2=64k23（4k2+1）=6431k2+4∈4，163，也就是t+1t+2∈4，163，由此可得

t∈13，1∪（1，3），由

λ=-35+165（5t-3）

，可得

λ∈（-∞，-3）∪-13，1∪（1，+∞）.

解法3：由于x1+x2=-16k4k2+1，x1x2=124k2+1，所以1x1+1x2=-43k.又由于k1=y1x1=k+2x1，k2=y2x2=k+2x2，且有k1=λk2，则1x1-λx2=λ-12k，由1x1+1x2=-43k，

1x1-λx2=λ-12k，对联立方程进行求解可得x1=-6（λ+1）（5λ+3）k，

x2=-6（λ+1）（3λ+5）k，由此方程组可知x1x2=36（λ+1）2（5λ+3）（3λ+5）k2=124k2+1，化简方程可得15λ2+34λ+153（λ2+2λ+1）=4k2+1k2=4+1k2.由k2＞34，可知15λ2+34λ+153（λ2+2λ+1）=4+1k2∈4，163，即有12（λ2+2λ+1）＜15λ2+34λ+15，

15λ2+34λ+15＜16（λ2+2λ+1），求解可得λ∈（-∞，-3）∪-13，1∪（1，+∞）.

3 结语

解析几何是高中数学教学中的重难点，在对其

进行讲解时，教师需科学合理地设计代数解析的方法，通过一题多解的形式，引导学生准确把握知识本质，促进学生知识结构的优化，从而使学生处于“一法通解”的聚焦性思维当中，实现自身解题能力的提高.

参考文献

［1］张小凤.浅谈高中数学解析几何的解题技巧和策略［J］.理科爱好者（教育教学），2022（1）：118-119.

［2］杨冬梅.试论高中数学解析几何问题的教学方法［J］.理科爱好者（教育教学），2021（5）：100-101.

［3］徐海棠.高中数学解析几何问题的解题技巧［J］.数理化解题研究，2020（25）：40-41.

［4］陈志恩.高中数学解析几何综合应用解题策略［J］.天津教育，2020（20）：151-152.

［5］黄志熇.高中数学解析几何问题的解题技巧探究［J］.试题与研究，2020（2）：31.

［6］邱笑宁.高中数学解析几何解题策略研究［J］.教育界（基础教育），2018（8）：92-93+112.