选编“好的问题”，践行“三学”课堂

“自学·议论·引导”教学法倡导“三学”（即学材再建构、学法三结合、学程重生成），在新授课中，特别是单元教学中实践较多。近一段时间以来，笔者用较多的时间和精力在九年级开展课堂教学与研究，对九年级复习课有较多的实践和思考。本文以九年级“与圆有关的位置关系”复习课为例，谈谈如何选编“好的问题”，践行“三学”课堂。

一、“与圆有关的位置关系”复习课教学设计

活动1：过一点作圆的切线

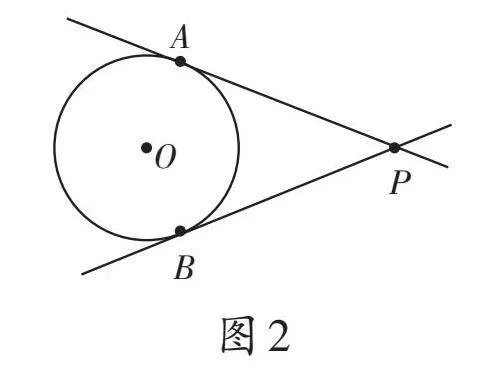
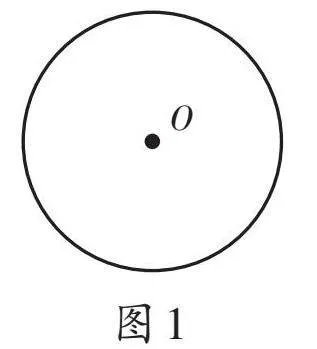
问题1：已知⊙O，如图1，过一点P，画出⊙O的切线。

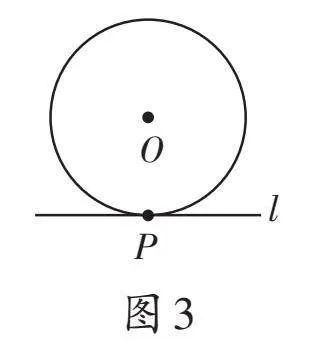
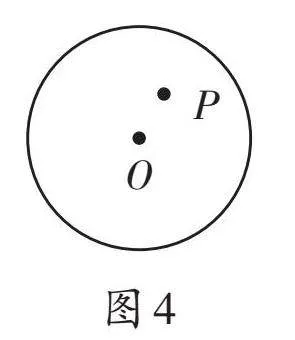
教学预设：这是一道“结构不良问题”。当学生发现在所给的图1中没有点P时，教师可及时引导：“同学们，你们可在图1中添出一个点P，继续求解。”这时学生就会想到需要分类讨论（如图2—4）。在三种点和圆的位置关系出示之后，教师可顺便安排学生复习点到圆心的距离d与半径r的大小关系（为节约用时，教师可以提前准备PPT以配合学生讲解）。在图2中，点P在⊙O外，过点P可以画出两条切线；图3中，点P在⊙O上，过点P可以画出一条切线；图4中，点P在⊙O内，过点P不能画出切线。特别是，结合图4，学生会说出过圆内一点P不能画出圆的切线，教师可追问：“能否画图演示，为什么不能画出圆的切线？”学生可能会过点P画出圆的割线，看出此时画的线与圆有两个公共点，不符合圆的切线定义，顺势也就复习了圆的切线、直线和圆的位置关系的相关知识。教师可结合PPT呈现相关知识结构图（或思维导图）。

需要说明的是，《义务教育数学课程标准（2022年版）》将尺规作图“过圆外一点作圆的切线”作为选学内容，所以我们先安排的是“画切线”活动，然后结合学情，相机安排学生“用尺规作图，过圆上一点或圆外一点作圆的切线”。教师还可预设不同的作法，如文献[2]中的教学实践，作为教学引导时的“备用”。

活动2：切线长定理及基本图形的研究

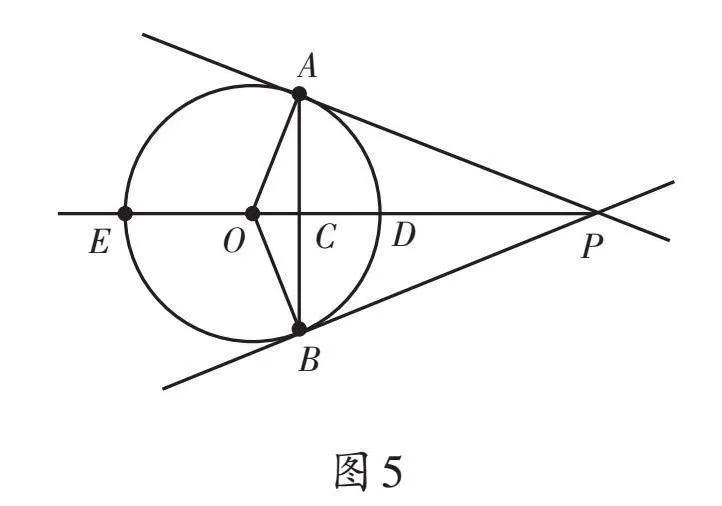
问题2：如图5，PA、PB是⊙O的切线，切点分别是点A、B，射线PO交⊙O于点D、E，交弦AB于点C，你能找到哪些相等的线段和哪些相等的角？

教学预设：教师组织学生复习切线长定理时，可安排学生分组交流后，再在班级内进行汇报展示。如果学生讲解图5中相等的线段或角比较“杂乱、无序”，教师可追问其他学生“能否更加有序地说说，以便不重不漏”。教师在点评时，要注意从轴对称（对称轴是直线PO）和全等三角形的角度进行小结。顺便指出，若是中考复习课，教师还可从相似的角度追问：“图中有相似三角形吗？举例说说。”

活动3：三角形的内切圆和外接圆

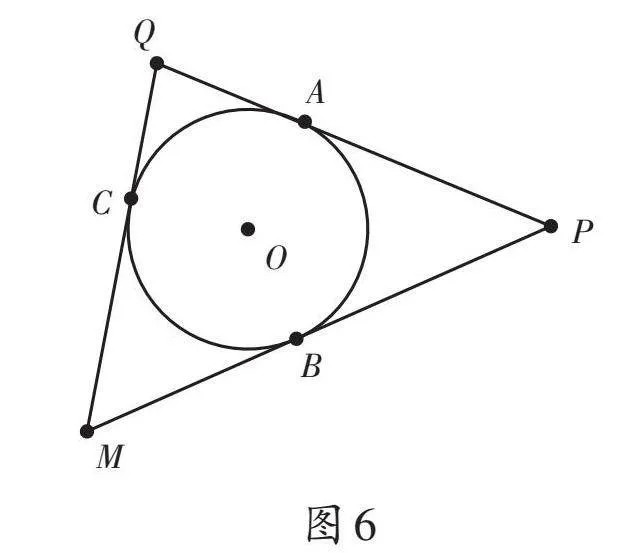
问题3：（在图2的基础上）如图6所示，在⊙O上取一点C，过点C作⊙O的切线，并与⊙O的切线PA、PB相交于点Q、M。结合图6，你想到了哪些数学概念？

教学预设：这是三角形内切圆的基本图形，学生能联想到三角形内切圆、内心等数学概念。这时教师可根据学情，继续安排以下几个小问题，帮助学生复习三角形内切圆的相关知识或性质。

（1）任意画一个△ABC，如何用尺规作图作出它的内切圆？（学生在小组内交流构图思路和作法，然后教师安排学生口头汇报作法步骤即可。教师也可以根据教情、学情，相机安排学生在黑板上进行作图演示。）

（2）如图6，若△PQM的周长为12，内切圆的半径r=1，求△PQM的面积。

（3）若图6中，QM=9，PQ=13，PM=14，求PA、QC、MB的长。

以上几个问题都是新授课期间教材上曾出现的例题、习题，复习时应该不会耗时太多。如果学情较好，“问题3”的以上设问也不必全部呈现，以“开放式问题”代之，比如“请同学们结合图6，设计一个问题并交流，有兴趣的同学可以在课后深入研究”。

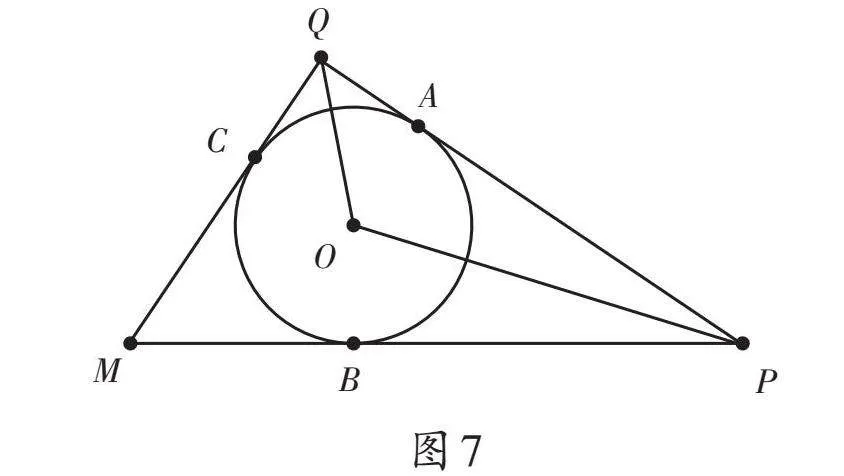
问题4：如图7，在Rt△MPQ中，∠PQM=90°，⊙O是△MPQ的内切圆，切点分别为点A、B、C。

（1）当∠MPQ=40°时，求∠POQ的度数。

（2）若AP=6，MC=4，请设计一个问题，先在小组内交流，再在班级内展示设计意图与求解思路。

教学预设：第（1）问可直接根据三角形内角和、角平分线性质求解；第（2）问比较开放，教师要充分预设学生可能的设问，如求Rt△MPQ各边长、图7中所有线段的长、内切圆⊙O的半径、三角形PQM的周长与面积，等等。在学生交流展示各组的设计问题之后，教师给出以下追问，将问题进一步变式拓展。

追问1：上面已经复习了三角形的内切圆及作法，同学们想一想，怎样作出一个三角形的外接圆呢？图7中，有比较快的方法作出直角三角形MPQ的外接圆吗？

教学预设：通过“追问1”，顺势复习三角形的外接圆、外心等数学概念。学生熟悉相关作法，而图7中的△PQM是直角三角形，作出其外接圆的较快的方法是先确定外心（斜边PM的中点），这样就可以很容易地作出△PQM的外接圆了。

追问2：在上面第（2）问的条件下，设O′是△MPQ的外心，求OO′的长。

教学预设：“追问2”的本质是分析“三边分别为6、8、10的直角三角形的内心与外心之间的距离”。

活动4：课堂小结

小结问题1：今天我们复习了点和圆、直线和圆、三角形和圆的位置关系，我们是如何来研究的？哪些问题给你留下了较深的印象？

预设：本节课我们是从“过一点，画圆的切线”开始，依次复习了点和圆的位置关系、切线长定理、三角形内切圆和外接圆，并且复习了一些典型习题。

小结问题2：研究一个图形（如点、线或三角形）与圆的有关位置关系，你积累了哪些经验？

预设：如研究图形的组成元素与圆的组成元素之间的位置关系，这些关系对应着一定的数量关系。

小结问题3：四边形一定有内切圆吗？四边形一定有外接圆吗？如果一个四边形既有内切圆，又有外接圆，那这个四边形的边、角之间有什么样的关系？请有兴趣的同学课后深入研究。

预设：四边形不一定有内切圆，也不一定有外接圆。如果一个四边形既有内切圆，又有外接圆，这样的四边形对角互补，对边之和相等。

二、教学立意的进一步阐释

1.选编好的问题，让画图活动驱动复习进程

关于如何选编“好的问题”驱动教学进程，文献[3]中提出“好的问题”要有“数学味”“尽量串联整节课”。想来，本文关注的这节复习课各个环节的问题设计也追求了上述特点。比如，开课阶段，笔者安排了一道“结构不良问题”（过一点，画出圆的切线），对于思维不严谨的学生，教师可以先安排小组交流，以完善他们的认知，然后通过全班学生交流，展现学生对这个问题的“完整思考”；在后续复习进程中，笔者始终围绕“活动1”画出的图形进行变式、改编，整节课都围绕着开课阶段得出的基本图形渐次展开、由浅及深，实现了好的问题（伴随画图活动）驱动整节课的复习进程。

2.预设开放式问题，用相机追问凸显复习深度

郑毓信教授多年前就倡导“从开放题走向开放式教学”。然而我们看到的不少复习课中，由于使用了大容量的习题单式的导学案，使得复习课成为“一题接着一题”的习题讲评课，虽然在一些习题的讲评过程中有些师生的对话，但大多停留在“师问生答”的较低层面，整体上看，教学过程是比较封闭的。为了让教学从封闭走向开放，我们在上述课例的教学设计中安排了多处的“开放式问题”，除了上述提到的开课阶段的“结构不良问题”（也可看成开放式问题）外，“问题2”“问题3”“问题4”在题干呈现之后，都安排了开放式问题，促进了后续的开放式教学。值得一说的是，这些开放式问题，并不是简单放手，也不是上课时任由学生“踩着西瓜皮，滑到哪里是哪里”，而是需要教师在课前充分预设学生可能的回答以及教师要给出什么样的点评或追问，特别是通过恰到好处的追问，凸显和追求复习的深度。

3.构思小结问题，帮学生梳理、回顾复习内容

复习课的教学时间常常难以把控，往往因为有些较难问题的课堂展示、点评用时偏多，就会挤占课堂小结的时间。笔者建议，教师在课前就要精心构思“小结问题”，让小结问题帮助学生梳理回顾整节复习课的内容。特别地，要通过“小结问题”与前面的各个复习课进行关联、呼应，使其成为复习课不可或缺的重要环节。如上文“小结问题1”安排学生回顾本节课是如何复习的，“小结问题2”让学生梳理、积累研究几何问题的方法与经验。当然，作为必要的拓展与研究展望，笔者还预设了“小结问题3”，让学余有力的学生继续探究、挑战“既有内切圆又有外接圆的四边形的性质”。需要指出的是，像“小结问题3”这样的课前预设，也需要像“课中”很多预设的追问一样，根据教情、学情相机呈现，有的放矢。想来，这也是“预设要大于生成”的一种备课追求吧。

【参考文献】

［1］中华人民共和国教育部.义务教育数学课程标准（2022年版）［M］.北京：北京师范大学出版社，2022（4）．

［2］王强.基于确定性下的尺规作图［J］.中学数学杂志，2021（8）：58-61．

［3］刘东升.我们需要怎样的“问题”驱动课堂——由美国莎维女士执教的函数图像课说起［J］.教育研究与评论（课堂观察），2016（11）：65-68.

［4］郑毓信.“开放的数学教学”新探［J］.中学数学月刊，2007（7）：1-4．

本文系江苏省教育科学“十四五”规划课题“高质量发展视域下‘三学’立人的实践研究”（课题编号：TSXM/2021/06）阶段性研究成果。

（作者单位：1.江苏省南通市启秀中学；2.江苏省南通市教育科学研究院）