贴近主线并聚焦目标:单元复习课的选题追求
钱后义


摘要:七年级的综合题中有一类“数轴上双动点”问题,更适合在七年级上学期期末阶段的复习选用,而不太适合在有理数或整式加减这两章就急于选、练、讲.这类“数轴上双动点”综合题的解题关键是“数形结合”,将动点所对应的“数”(用含未知数的字母)表示出来,然后抓住运动中的等量关系列出方程求解.
关键词:贴近主线;聚焦目标;单元复习课;数轴双动点习题
最近,学校教导处组织工作三年之内的年轻教师上汇报课,笔者有机会参加听课、评课活动.教学内容是七年级上学期有理数和整式加减两章的复习.老师们精心备课、精彩展示,看得出年轻教师努力上进的专业追求.当然,教学是遗憾的艺术,其中有一位教师在复习课的学案上选编了一道数轴上的双动点综合题,虽然也有少数学生在课堂上能挑战成功,并与全班讲解分享,但这道习题的讲评并没有突出数轴的本质,解法也只是重复了小学阶段行程问题的思路,不够贴近本课复习目标.本文中先概述笔者的观课与随感,然后给出单元复习课选题的建议和教学思考,供讨论.
1 数轴上双动点习题讲评及听课随感
习题 如图1,在数轴上有C,D两点,它们分别对应着数-10,5.现有一只电子蚂蚁H从点C出发,以每秒1个单位长度的速度沿数轴负方向向左运动,同时另一只电子蚂蚁Q从点D出发,以每秒4个单位长度的速度沿数轴负方向向左运动.
(1)设两只电子蚂蚁在数轴上的点E处相遇,求点E对应的数;
(2)经过多少秒,两只电子蚂蚁在数轴上相距9个单位长度,并求此时电子蚂蚁Q在数轴上对应的数.
学生独立练习5 min左右,教师挑选了一个学生的解题过程进行投影,并安排学生Z上台讲解:
第(1)问,两只电子蚂蚁的初始距离即C,D两点间的距离是5+10=15个单位长度,两只电子蚂蚁在15÷(4-1)=5秒后相遇.所以点E对应的数是5-4×5=-15.
第(2)问,当两只电子蚂蚁未相遇时相距9个单位长度,它们的相遇时间为(15-9)÷(1+4)=1.2秒,这时电子蚂蚁Q所在点表示的数为:5-1.2×4=0.2.
当两只电子蚂蚁相遇后相距9个单位长度时,它们的相遇时间为(15+9)÷(1+4)=4.8秒,这时电子蚂蚁Q所在点表示的数为:5-4.8×4=-14.2.
老师听了之后连连摇头说:“第(2)问的解答不正确,
你把动点问题浅显地看作行程问题来解,十分容易出现把公式套用错误的情况,比如你就把追及问题当作相遇问题,两点相向而行来思考,大错特错了!”
于是学生Z重新画图分析后,修正第(2)问的答案如下:
如图2,当两只电子蚂蚁未相遇时相距9个单位长度,它们的相遇时间为(15-9)÷(4-1)=2秒,这时电子蚂蚁Q所在点表示的数为:5-2×4=-3.
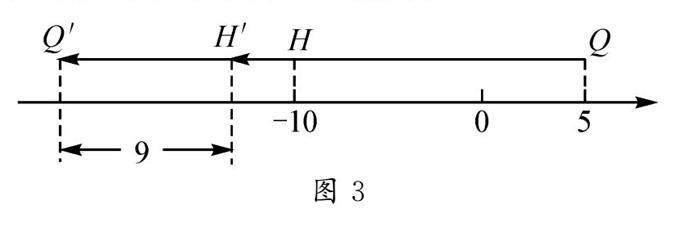
如图3,当两只电子蚂蚁相遇后相距9个单位长度时,它们的相遇时间为(15+9)÷(4-1)=8秒,这时电子蚂蚁Q所在点表示的数为:5-8×4=-27.
听课随感:近年来,这类动点问题在七年级上学期比较“流行”,且不论这些流行的“人为编造”的数学习题是否“有趣”或“无趣”.观课中可发现学生Z在小学阶段已深刻理解行程问题,当动点问题“生长在”数轴上,他能迅速转化为小学阶段就很熟悉的行程问题,不必管数轴的“包装”,排除干扰,善于转化,精选工具(算术),快速解决.遗憾的是看错行程问题的类型,导致错误,随后教师点评并启发“以形助数”,在图形直观启示之下,解题步骤展现出“让思维可见”的“好的表达”!
对于执教老师的课堂表现来说,也显得教法相对“单一”,比如从上文观课记录可以看出,该教师与学生Z的对话基本上是“一对一”的,忽略了其他同学的课堂参与.如果教师在学生Z出错后,能围绕这个错误、化用这个“错误资源”,组织全班同学讨论、纠错并究错,则会是一次更有价值的“化错教学”(小学数学特级教师华应龙老师积极倡导).
本质上说,上述方法仍然是小学阶段就已经(或应该)训练了的,还没有显示出数轴作为“数形结合”重要工具的价值.比如,我们可以设运动时间为t秒,则点H,Q对应的数分别是-10-t,5-4t.由两点间的距离公式,可得HQ=|(-10-t)-(5-4t)|=9,化简得|3t-15|=9,即3t-15=9或3t-15=-9,解得t=8或t=2.
这种思路能很好地体现了数轴上的点与所对应的数(含t的式子表示)之间的关系,然后借用两点之间的距离公式列出含绝对值的方程,这些知识或解法背后展现的数学思想对于八、九年级的函数问题,或者坐标系下的求解都是非常有发展性的.当然,由于学生才学到有理数、整式加减这两章,上述“好的方法”(更体现数轴价值)可能涉及到方程的解法,“急于抛出”这种解法有“超进度”之嫌,待整式加减、一元一次方程学习之后的阶段复习或期末复习,再适当安排专题讲评,或许是更合适的选择.
2 关于单元复习课选题的几点思考
(1)选题之前要明确单元复习的目标
单元复习课的教学设计或备课要明确教学目标,而不只是罗列知识点、选几道例题和习题就是备课工作.具体来说,围绕单元复习课的内容,查阅课程标准和教材,然后拟定3~4条复习目标(复习课的教学目标不同于新授课).比如,数轴、相反数、绝对值这些内容在新授课时的教学目标就要细化处理,而在有理数单元复习时,往往只是一句话“理解有理数及相关概念”.再如,整式加减中第1课时学习单项式、多项式及相关概念时,有很多零碎的知识点,在单元复习时只能浓缩为“理解整式及相关概念”,而需将有理数、整式的运算作为阶段复习或单元复习的重要目标进行表述.
(2)选题改编要围绕单元复习的重点
在明确了复习课的教学目标之后,选题就要围绕教学目标有序展开,由易到难、渐次展开.以有理数、整式加减的阶段复习课为例,复习重点应该是有理数、整式加减的运算,这节课中选题的重心也要落在运算上.具体来说,例习题的选编要体现在运算上,但并不全部是以前练习过的运算习题的拼凑,反复练容易形成审美疲劳,也是一种“内卷”.教学中可以将运算训练类习题进行变式改编,比如摘选新授课期间学生的一些运算错误进行展示,安排学生参与纠错、究错[1],并交流运算心得或分享经验.再如,数学来源于生活、服务于生活,针对有理数、整式加减的复习重点,还可适当选编生活实际问题,让学生运用这一阶段所学习的内容、工具、模型来解决问题,突出应用能力、数学建模能力的训练.
(3)较难题内容效度要聚焦本课主线
复习课在“后半段”一般都会选编一、两道较难的例习题,以便让学生在问题渐次展开的过程中,由易到难、拾级而上[2]、挑战自我.这些较难题的选编非常考验教师备课选题的基本功,很容易出现随手选编“流行考题”“名校考题”之类的做法,而这些考题往往来源于期末试卷(甚至是中考试卷),其命题人对这些题的命题定位是整个学期(或初中学段),这样选编成单元复习时这类问题的内容效度往往有较大的偏差.比如上文提及的数轴上的双动点问题,在有理数、整式加减之后就匆忙选编训练就不太恰当,因为这类问题“较好的解法”(或者有“初中味道”的方法)需要学生有扎实的方程、线段和差倍分等知识储备.又如,学生在初学全等三角形之后,有些教师对一些同步教辅书上的习题不加取舍,没有认真研究教材上新授课期间全等三角形的习题要求,人为拔高全等三角形的练习难度,增加学生对几何学习的畏难情绪.
参考文献:
[1]华应龙.华应龙与化错教学[M].北京:北京师范大学出版社,2015.
[2]刘东升.问题驱动渐次展开,开放对话查漏补缺——以勾股定理复习课为例[J].中学数学,2021(18):6-7,75.

