一道含参不等式恒成立问题的多种解法
高晓航
【摘要】含参不等式恒成立问题作为高考中固定的一类综合性问题,因为思维难度高、知识容量大,所以对学生逻辑思维和数学运算等能力的要求较高.文章以一道高考模拟题为例,讨论含参指对混合型不等式恒成立问题的求解策略,最终给出四种方法:分离参数法、隐零点求最值法、图像法和放缩法.
【关键词】不等式;恒成立问题;求解策略
引 言
含参不等式恒成立问题以导数相关知识为背景,难度较大,需要学生善于观察,灵活转化,转化的形式和方法也不是一成不变的,因此此类题目的知识与能力的承载性极强.下面以一道高考模拟题为例,介绍此问题中特殊的一类:含参指对混合型不等式恒成立问题的四种解题方法.
一、题目呈现
已知函数f(x)=ex-x,g(x)=alnx+a,(a>0,e是自然对数的底数).
(1)若直线y=kx与曲线y=f(x)和y=g(x)都相切,求a的值;
(2)若f(x)≥g(x)恒成立,求实数a的取值范围.
本题第(1)问较为常规,利用导数的几何意义分别求出两曲线y=f(x)和y=g(x)过原点的切线,联立即可求得参数a的值.并由a=e-1可求出x2=x1=1,即两曲线切于同一点,为第(2)问含参指对混合型不等式恒成立问题做铺垫.第(2)问考查的知识点较全面、逻辑性强,下面运用不同解法对该问题进行探究.
二、解法探究
解法1 分离参数法
因为ex≥x+1>x,
所以f(x)=ex-x>0恒成立.
由f(x)≥g(x),
得到ex-x≥a(lnx+1),
所以先讨论g(x)≤0的情况.
综上,a的取值范围是(0,e-1].
评注:分离参数法,即把参数放在不等式一边,对另一边构造函数,由此可将含参不等式恒成立问题转化为函数最值问题.只需进一步研究所构造函数的单调性,求出最值,即可得参数取值范围.分离参数法是处理此类问题的最基本方法.
解法2 隐零点求最值法
综上可知,当a∈(0,e-1]时,f(x)≥g(x)恒成立.
评注:不等式恒成立问题的一个常规思路是:将不等式一侧化为0,对另一侧构造新函数,此时该问题就转化成了函数最值问题.但是若该不等式含参,那么构造的新函数依然是含参函数,无法用导数工具直接求出最值.可以尝试通过判断含参函数的导函数是否存在“隐零点”,借助隐零点存在范围,判断所构造含参函数的最值.“隐零点”与“显零点”相对,指函数的零点虽然存在,但无法直接求出,通常可以利用零点存在定理判断,不满足此定理条件时可针对具体图像分析.
解法3 图像法
此题可以运用图像法来解决,首先需要判断函数图像的凹凸状态.
函数f(x)=ex-x,利用求导判断函数单调性,即f′(x)=ex-1,令f′(x)=0得到x=0.
所以当x∈(0,+∞)时,f′(x)>0,f(x)单调递增,
由此可画出函数f(x)的大致图像,f(x)图像呈向下凹的状态.
然后判断函数g(x)图像的凹凸状态.
其中,g(x)=alnx+a,a>0,这里的参数a对函数g(x)=alnx+a,a>0图像的大致形状没有显著影响,只改变图像的“胖瘦”和高低位置,则函数g(x)的图像与对数函数y=lnx的图像走势大致相同.
这样函数f(x),g(x)的图像呈凹凸反转的状态.那么随着参数a的变化,函数f(x)与g(x)有一个临界位置,此时两个函数均与一条直线相切(如图所示),该切线即为第(1)问中求得的直线:y=(e-1)x.随着参数a的增大,函数g(x)的部分图像将在f(x)图像上方.
所以f(x)≥g(x)在x∈(0,+∞)上恒成立时,参数a∈(0,e-1].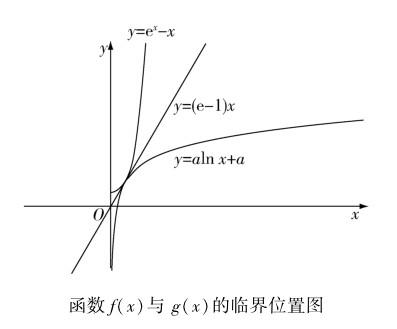
评注:此法简洁自然,三步即可确定答案.当两个函数解析式中分别含有指数和对数时,由于指数函数和对数函数图像本身凹凸反转的特点,因此可以通过分析或者求导判断题目中复合函数的图像是否也会呈现凹凸反转的情况,此时可以首选图像法.通过改变参数的值使两个函数相切,以找到切点,即找到不等式成立的分界点.当不等式较为复杂时,那么图像法的关键就在于对其进行恰当转化,此处的变形是基于常见的指对同构联想到的,目的是使不等式左右两边函数的图像呈现凹凸反转的情况,同理继续找两函数图像的切点即可.
评注:由于一些特殊的指数函数、对数函数与一次函数三者图像之间具有临界位置关系,所以放缩法是解决含参指对混合型不等式恒成立问题的一个巧妙方法.但是针对不同题目,放缩的选择不同,没有固定的放缩策略.这就需要解题者在对一些典型不等式熟悉且能运用的情况下,有较多的知识储备、放缩的意识以及灵活的思维.若能巧妙运用放缩,将能够快速、轻松解决含参指对混合型不等式恒成立问题.
结 语
从以上四种解题方法可以看出,解决含参指对混合型不等式恒成立问题的关键在于灵活运用函数思想:分离参数法和隐零点求最值法都是将不等式恒成立问题转化为函数最值问题,图像法是将不等式恒成立问题转化为函数图像问题,放缩法也可以看作是将不等式恒成立问题转化为两个具有临界位置关系的特殊函数图像问题.同时其中也蕴含着函数性质问题、函数对应方程的根的分布问题等.除函数思想外,数形结合、等价转化、分类讨论等也是解决此类问题常用的思想方法,需要学生有意识地灵活运用.
【参考文献】
[1]林国夫.2013年高考导数综合应用中的“隐零点”[J].中学数学杂志,2013(9):49-52.
[2]朱秀媛.凹凸反转解决关于lnx与ex的证明题[J].数学学习与研究,2019(2):101.
[3]孙鹏飞.用放缩法巧解函数不等式恒成立[J].数理天地(高中版),2023(5):6-7.
[4]袁源.求解含参不等式恒成立问题的几种途径[J].语数外学习(高中版上旬),2023(1):45-46.
[5]熊勇.由一道题谈求解含参不等式恒成立问题的思路[J].语数外学习(高中版下旬),2023(9):43-44.
[6]薛晋红.由一道题谈含参不等式恒成立问题的解法[J].语数外学习(高中版下旬),2023(5):39.
[7]叶琳玮,罗家贵.由一道题谈解答含参不等式恒成立问题的路径[J].语数外学习(高中版下旬),2022(8):42-43.
[8]吴勇.由一道含参不等式恒成立问题引发的思考[J].语数外学习(高中版中旬),2021(8):45.
[9]梁王海.多思维化归,四方法破解———一道含参不等式恒成立问题[J].数学学习与研究,2021(2):111-112.
[10]汪亚运.一道含参不等式恒成立问题的多角度探究[J].中学生数学,2020(19):41-43.
[11]张虹.一道含参不等式恒成立问题的多种解法及分析[J].中学数学月刊,2016(2):53-55.

