化工原理教学中数学建模能力的培养

宋梁成 朱崇强 杨春晖

摘    要：数学模型法是一种重要的科研方法与解决实际问题的途径，在化工原理课程的教学中多有涉及。鉴于此，应将数学建模能力的培养确定为该课程教学目标点之一，在教学中系统地融入数学建模过程，以课程的教学内容为载体讲解数学建模方法与要点，以具体的实际案例训练学生的数学建模能力，引导学生掌握科学的研究方法，培养并提高洞察力和想象力，从而激发出创造力，助力化工行业创新型人才的培养。

关键词：化工原理；数学建模；能力培养；案例教学

中图分类号：G642    文献标识码：A    文章编号：1002-4107（2024）06-0046-03

一、背景

（一）数学建模的意义

数学建模是在充分认知复杂过程的基础上进行合理简化后建立数学模型解决问题的研究方法，在推动科学技术发展的过程中起到了重要作用。2 000多年以前，欧几里德创立的几何原理与17世纪牛顿发现的万有引力定律都是科学发展史上典型的数学建模范例[1]。马克思说过，一种科学只有在成功地运用数学时，才算达到了真正完善的地步[2]。数学是各学科可以共同使用的一种科学语言，时代发展和科技进步的大潮推动数学科学迅速进入各个领域。以数学方法和计算机技术为核心的工艺研究与装备制造已经成为化学工业的主要手段[3]。化工生产过程中的优化过程也是通过数学建模进行实现的，比如原料配比、产品生产工艺、产品设计、优化过程以及化工产业应急管理评价等[4]。

（二）培养学生数学建模能力的意义

数学建模是数学和实际问题的桥梁，这个桥梁的构建需要多方面的能力。面对一个实际的过程或现象，经过仔细分析后，能够迅速抓住问题的关键点和主要因素，这需要的是洞察力与分析归纳能力。在掌握表观现象的基础上，能够抽象地构建出相应的模型来描述这个过程，这需要的是想象力。数学建模能力的培养有助于学生对知识的本质实现高阶认知，提高建模能力是培养学生运用数学知识分析解决实际问题的一种有效手段。

（三）化工原理课程培养学生数学建模能力的必要性

课程教育的目的是在传授知识的基础上培养学生的能力。化工原理课程的教学目的，不仅仅在于向学生传授化工理论与单元操作的基本知识，更重要的是让学生掌握科研方法与培养学生解决实际问题的能力[5]。而数学建模研究方法是化工原理课程最为常用的两种研究方法之一。因此，在化工原理的教学过程中应结合课程内容融入数学建模教学。本文以两个数学模型的应用案例在教学过程中进行数学建模方法及经验的介绍，以生产生活中的实际案例培养并训练学生通过数学模型法解决实际问题的能力，将数学建模教学渗透于化工原理教学的全过程，引导学生掌握科研方法，提高学生的科研能力，助力化工行业创新型人才的培养[3]。

二、数学建模

（一）基本方法

数学模型一般是实际事物的一种数学简化。数学建模就是根据实际问题建立数学模型并在求解之后依据结果去解决实际问题的过程。建模方法包括机理分析法和测试分析法，机理分析法是根据对客观事物特性的认知找出反映内部机理的数量规律，建立有明确物理或现实意义的模型，可以看作是一个“白箱”模型。测试分析法是将研究对象看作一个“黑箱”模型，是通过对输入输出数据的测量与系统分析，按照一定的准则找出数据拟合最好的模型。数学建模的成败关键在于能否对真实的過程进行合理的简化，得到一个可以用数学方程来描述的物理模型。要做到这一点，就需要对过程的变化规律足够了解，并能够抓住该过程的主要因素，进行大胆且合理的简化，而不是将原型原封不动地复制过来。模型只要求反映与某种研究目的相关的那个方面的特征，使得模型在研究的某一方面与实际过程保持等效。

（二）主要步骤

数学建模过程的主要步骤如下。

1.对真实的复杂过程进行系统的分析。充分认知并掌握其复杂特性，在此基础上分析得出将要简化的方向。

2.对真实过程的复杂因素进行合理的简化。确定并建立能够用数学方程来描述的该过程的物理模型，该模型能够真实反映各主要因素之间的定量关系。

3.对简化的物理模型进行数学描述，即进行数学建模。数学模型不能全面完整地描述实际过程，但能反映实际过程中主要因素间的相互关系。

4.确定模型参数。数学中的模型参数往往具有一定的物理意义，但这个参数却很难得出，模型参数是数据拟合过程的待定参数，可通过实验确定；或将模型参数与过程中的物理量进行关联，通过测定实验物理量而确定模型参数。

5.模型求解与校验。数学模型求解的结果要回带相关的过程案例，确定是否能够在一定程度不失真的条件下解决实际问题。

三、课程内容中的数学模型研究案例介绍

本文以案例教学的形式介绍如何结合化工原理课程教学内容渗透讲解数学建模研究方法。以流体通过颗粒床层的阻力计算案例向学生讲述数学建模过程需要深入的洞察力与分析能力；以相际对流传质机理的研究历程案例向学生展示研究者是如何发挥想象力构建不同的模型并逐步完善推进该领域的研究进展。

（一）流体通过颗粒床层阻力的计算

过滤操作过程中流体流过床层的压降是实际工程中一个十分重要的物理量，但流体流经如此复杂通道时的压降却是无法依照实际流动状态进行计算的，可以通过数学模型法来进行简化求解。首先分析该问题，流体流经床层的压降主要来源于两部分：一部分是流体与颗粒表面间的摩擦所产生的压降；另一部分则是流动过程中孔道截面突然扩大或缩小等产生的形体阻力压降。观察过滤操作的实际过程可以发现流体流经床层孔道的横截面积较小且流速较慢，是处于雷诺数极低的状态下流动，此条件下摩擦阻力压降起主导作用而形体阻力压降可以忽略。抓住问题的关键因素后，可以将流体流经床层的压降简化为摩擦阻力压降进行求解。把流体流过复杂孔道流动状态中压降的求算简化成流体流经直管时摩擦阻力的计算，这样就建立了可以以直管摩擦阻力公式进行数学求解的物理模型。所建立的模型虽是实际过程的简化，但在摩擦阻力计算方面要与真实过程等效，所以要根据实际过程来确定简化模型的参数。摩擦阻力主要受流体与床层之间的接触面积及其流动状态两个参数影响，简化后的模型要保证这两个参数与实际过程一致，即简化后的直管束的流通截面积要与实际床层的平均自由截面积相等，且润湿周边长也与床层自由截面的平均润湿周边长相等。进一步分别将流通截面积与润湿周边长对床层高度进行积分，也就得到了简化后的管束模型的床层空隙率以及比表面积要与实际床层相等，据此可以求出简化后模型的床层当量直径，见公式（1）[6]。其中ε为床层的孔隙率；   为床层的比表面积。

获得颗粒床层的当量直径后，依照直管摩擦阻力公式计算出流体流经床层的压降，将流体在床层内实际流速换算成空床时的表观流速即可得到公式（2）[5]，

该公式即为流体通过颗粒床层的压降的数学模型。这样在讲解流体通过床层的压降知识点时，将数学建模的全过程展现给学生，重点讲解数学建模的方法与要点。该数学模型的构建是在观察并掌握流体通过床层的流动特征基础上，对流体流动阻力的特征进行分析后忽略掉在极低雷诺数下的形体阻力而简化建立的，由此不难看出数学模型的建立需要敏锐的洞察力。

（二）相际对流传质机理的研究过程

化工单元操作当中的吸收、蒸馏与萃取等都是气液两相间的对流传质过程，即相际对流传质过程。相际对流传质过程的传质机理非常复杂，也一直是化工领域的研究难题。相际传质过程可以分为三个步骤：某组分从一相主体扩散到相界面，在界面中转入另一相，由相界面扩散到另一相的主体。依据相际传质过程步骤，1923年Whiteman提出了双膜模型，即停滞膜模型[7]。该模型的要点在于分析相际对流传质过程阻力分布特征之后，将整个过程的传质阻力简化于相界面两侧的停滞膜内。该模型认为在停滞膜以外的湍流主体中浓度处于均匀状态无传质阻力；同时相界面处于平衡状态也无传质阻力。而停滞膜内其传质的机理为分子扩散，这样就能够以停滞膜内的定态分子扩散过程来定量描述相际对流传质过程，其模型参数为相界面两侧的气膜厚度与液膜厚度。该模型的要点在于传质过程要有固定的相界面，所以其适用范围略窄，仅适用于流速不高的两流体之间的传质过程。当两流体流速较高无法形成稳定相界面与停滞膜时，该模型与实际过程偏离较远。

由于双膜模型不能很好地解释高速流动流体的相机传质过程。1935年，Higbie又依据液相相界面的结构特征提出了溶质渗透模型，该模型认为液面是由无数微小的定期更新的流体微元构成[8]。气液两相接触前液相界面处的浓度与主体一致，当气液两相接触时液相界面瞬间达到与气相平衡态的浓度，而后液滴在相界面的停留时间内，溶质以不定态的方式向流体微元中渗透。停留时间结束后表面得到更新，重新开始溶质渗透过程。如此构建物理模型后，就能够以停滞时间为周期内的不稳态扩散过程来定量描述相际对流传质过程。其模型参数为流体微元在相界面内的停留时间。与双膜模型相比，溶质渗透模型更能准确地描述对流传质过程，但模型参数停留时间很难确定。

溶质渗透模型不只是模型参数难确定，而且模型计算结果与实际情况的吻合程度也不够好，因为各流体微元在相界面内的停留时间未必是均等的。因此，在1951年，Danckwerts引入数学中的概率论将溶质渗透模型进一步修正为表面更新模型[9]。该模型认为无论相界面上的液体微元暴露时间长短其被置换的几率是均等的，因此引入了相应的模型参数单位时间内表面被置换的分率，即表面更新率。表面更新率是一个与流体力学条件及系统的几何形状相关的量可以通过实验测定，而上述溶质渗透模型中的参数停留时间不可测定。这使得表面更新模型比溶质渗透模型更加前进了一步，但仍未彻底弄清相际对流传质的机理，有待进一步研究推进认知。虽然，目前的模型距离用于实际计算还有一定差距，但是有助于理解该过程的本质，为提供强化传质的思路起到积极的作用。

从相际对流传质机理的研究过程可以发现，数學模型法在研究过程中起到了关键的推进作用，加速了人们对其传质机理的认知。研究者在对过程进行分析认知的基础上进行合理假设构建出相应的物理模型，而后采用数学模型求解。模型的逐渐前进是源于研究者对过程认知的不断深入，更重要的是发挥充分的想象力，不断完善旧有模型或构建新的模型。不同研究者对过程的分析研究提炼的要点不同会创造出不同模型。一个过程的数学模型并不是唯一的，这需要发挥研究者丰富的想象力去创造。因此，教师在教学过程中不仅要培养学生观察洞悉的能力，更要培养其丰富的想象力激发其创造力，这是创新的源泉。

（三）双层玻璃的功效

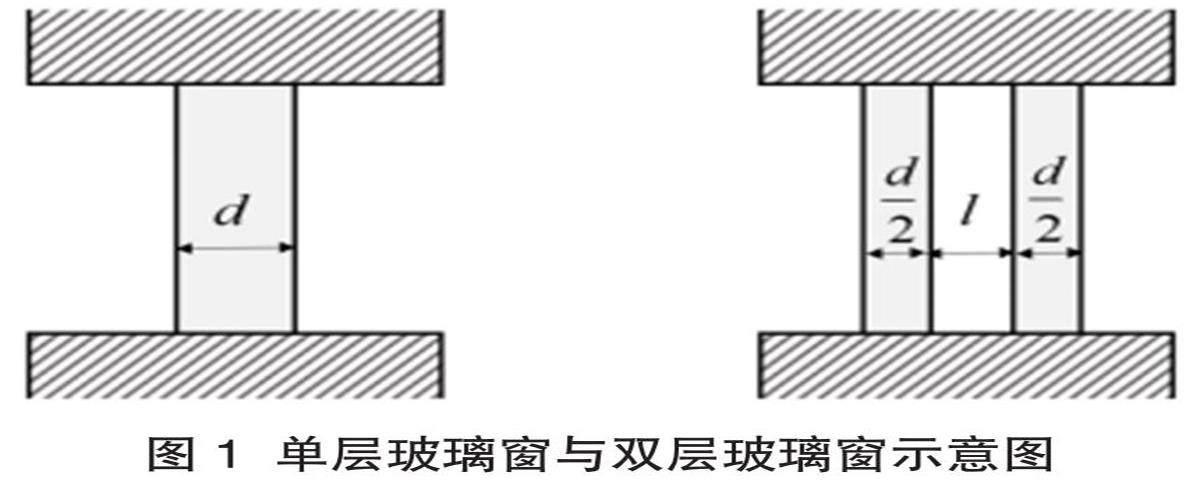
数学建模能力的培养包括洞察力、想象力、分析归纳能力以及逻辑思维能力的训练与提升。在以课程教学内容为载体讲解数学建模研究方法之后，可以以学生熟悉的生活案例或工程案例来训练和培养学生的数学建模能力。比如，在北方城市，近年来很多建筑物的窗户用的是双层玻璃，也就是如图1所示的两层玻璃之间为一定厚度的空气。这样设计的原因主要是减少热量向室外流失，起到保暖节能的效果。那么这样的设计具体能够减少多少热量的流失，该如何评价其保温效果，这就需要进行数学建模来进行定量分析。

进行数学建模首先要对实际过程进行系统分析，双层玻璃的传热过程并不复杂，机理清楚，是一个简单的“白箱”模型。热量在固态玻璃中的传热机理为热传导过程，而双层玻璃中间夹杂了一个空气薄层，即导热系数较小的物质，在膜层较薄的条件下可以认为该薄层内的空气流动很微弱，其对流传热的效果可忽略不计。所以即便空气是流体，但是因为膜层较薄空气流动很微弱，此时传热机理依然是没有宏观运动的热传导。这样进行适当合理的假设后获得的简化模型就是，原本的单层热传导变成了三层热传导。其物理模型的数学描述就叫傅里叶定律，在温度变化不大的条件下，材料的导热系数可以认为是常数或者使用定性温度下的导热系数。

因为传热的机理是热传导，所以采用傅里叶定律分别计算单层玻璃与双层玻璃的热量损失：（式1）单层玻璃上的热通量计算，（式2）双层玻璃上的热通量计算。式中Tin应为室内温度，Tout为室外温度，ks为玻璃的导热系数，kg记为气体的导热系数，d为玻璃层的厚度；l为空气层的厚度。

式2与式1相比得到式3，其结果反映了双层玻璃在减少热量损失上的效果。其中，常用的玻璃在-20～30℃的导热系数ks=0.756～1.0932W/m·℃，干燥空气的导热系数kg=0.0242W/m·℃，则ks /kg=31～45；常用的双层玻璃的l /d=2.25[10]。由此可以计算出Q2 /Q1≈0.9～1.4%，也就是双层玻璃比单层玻璃节约热量约98.6%以上。由此可以看出，双层玻璃的设计方案虽然工艺复杂制造成本略高一些，但能够达到相当可观的节能效果。将此案例拓展为三层玻璃，教师可以试问学生，为什么要设计三层玻璃而不是把传热系数较小的空气层设计更厚一些，这就涉及了模型成立的前提条件，如果空气层过厚空气热对流不可忽略，传热的机理不再是只有热传导而有对流传热，此时上述的传热模型不再适用，而且对流会强化传热降低保温效果。

四、结论

数学模型法是在充分认知复杂过程的基础上进行合理简化后建立数学模型解决问题的研究方法。本文以课程教学内容中的流体通过颗粒床层的阻力计算与相际对流传质机理的研究历程两个案例为载体系统讲解数学建模方法的过程与要点；以实际生活中的双层玻璃保温效果计算案例来训练数学建模能力。在化工原理课程的教学过程中系统地融入数学建模过程，能够培养并提高学生的洞察力与想象力，助力化工行业创新型人才的培养。

参考文献：

[1]  曹倩倩.新工科背景下高等数学“课程思政”教学案例的探索与实践[J].洛阳师范学院学报，2023（5）.

[2]  池志阳，谢明初，刘宇丹，等.数学价值观的内涵及其培养[J].数学教育学报，2023（2）.

[3]  李扬，谢彦红.基于化工专业需求的数学建模教学[J].化工高等教育，2009（4）.

[4]  郑锐泽.化工生产中数学建模的应用研究[J].化纤与纺织技术，2022（8）.

[5]  秦正龙.化工原理中常用工程方法研究[J].大学教育，2017（5）.

[6]  柴诚敬.化工原理（上册）[M].北京：高等教育出版社，2010：159.

[7]  WHITMAN W G.The Two-Film Theory of Gas Absorp-tion[J].International Journal of Heat and Mass Transfer，1924（5）.

[8]  HIGBIE R.The Rate of Absorption of a Pure Gas into a StillLiquid During Short Periods of Exposure[J].Trans.AICHE，1935（31）.

[9]  DANCKWERTS P V.Significance of Liquid-film Coeff-icientsin Gas Absorption[J].Industrial & Engineering Chem-istry，1951（43）.

[10]  吴春梅，郭险峰，赵勇，等.双层玻璃窗热性能研究[J].现  代商贸工业，2011（22）.

[责任编辑  姜    雯]

收稿日期：2023-11-23

作者简介：宋梁成，哈尔滨工业大学化工与化学学院副教授，博士

基金项目：黑龙江省教育科学“十四五規划”2022年度重点课题“一个平台四云驱动的工程专业人才培养方法研究”（GJB1422065）；黑龙江省教育科学“十四五规划”2023年度重点课题“基于校企协同的双创教育与专业教育融合与实践”（GJB1423127）；哈尔滨工业大学教学发展基金项目“化工原理课程教育教学改革”（XSZ2023051）

通讯作者：宋梁成