体悟图形运动，构建几何模型，提升核心素养

张丽君

【摘要】几何教学既是中考考查的重点，也是日常教学的难点，使用模型教学是几何教学的重要手段.本文以“倍長中线”模型为例，通过创设问题情境，体悟图形运动思想.借助典型例题，引导学生思考分析，构建8字型全等三角形模型.运用变式练习，进一步强化对模型的理解和应用，提高识图技能，发展数学观察能力，提升数学核心素养.

【关键词】图形运动；几何模型；核心素养

2022年颁布的《义务教育数学课程标准》提出数学课程要培养学生的核心素养是“会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界”.初中数学内容分为五大板块：数与数的运算、代数与方程、图形与几何、函数与分析、数据处理与概率统计.其中几何教学既是中考考查的重点，也是日常教学的难点，使用模型教学是几何教学的重要手段.

初中几何模型是教师在长期的教学实践中对具有一定相同特征的几何图形和问题的归纳，侧重对某一解题方法、技巧的模仿和迁移运用.本文笔者以沪教版教材八年级上册第十九章第2节“证明举例”中的“倍长中线”教学设计为例，阐述如何在图形运动思想指导下构建几何模型，提升核心素养.

1 课前思考

1.1 教学目标

依据学生的认知规律和思维水平，本节课的教学目标设置如下：能够识别模型，通过“倍长中线”构造8字型全等三角形模型，转化已知条件进而解决问题.进一步获得探究证明题思路的经历，丰富演绎证明的经验，体会在图形运动思想的指导下添置辅助线和构造模型的方法，感受转化思想.

1.2 教学重难点

学生在七年级已经学习过图形的三种运动、全等和等腰三角形的相关知识，为本节课的研究奠定了基础.本节课的教学重是点能够识别模型，通过“倍长中线”构造8字型全等三角形模型，转化已知条件进而解决问题；而如何利用“倍长中线”构造模型是本节课的难点.

2 课例设计

2.1 创设问题，引入模型

问题1 如图1，D是BC上的一点，BD=CD，∠1=∠2.能否证明AB=AC呢？

解法1

证明：因为BD=CD，∠1=∠2

所以AB=AC（等腰三角形三线合一）

解法2

证明：在△ABD与△ACD中，

所以△ABD≌△ACD（SAS）

所以AB=AC（全等三角形的对应角相等）

问题2 解法一和解法二的方法正确吗？错误在哪里？

问题3 在已有的图形和条件无法解决问题的情况下，我们需要怎么办？

问题4 如何添加辅助线？

设计意图 通过创设问题，引导学生思考两种证明思路存在的问题，复习回顾全等和等腰三角形的知识.学生分析发现无法在现有的图形中解决问题，引导学生体悟图形运动思想，利用将△ABD或△ACD旋转构造“8字型全等三角形”模型，从而达到转化边和角的目的.

2.2 分析归纳，构建模型

问题1 什么是倍长中线？

问题2 遇到什么情况需要构建倍长中线模型？

问题3 如何构建倍长中线模型？

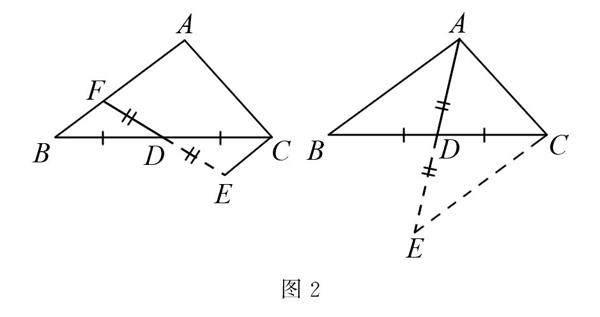
如图2，当题目中出现中点时可以想到延长三角形的中线或过中点的线段（类中线），使得延长后的线段等于原来的两倍，再联结相应的端点构造8字型全等模型，从而达到转化边和角的目的.

设计意图 引导学生归纳“倍长中线”的含义，提升数学语言表达能力.当已知条件中出现“中点”、“中线”时可以考虑倍长，构造8字型全等.通过分析归纳模型的特点，帮助学生在脑海中构建模型，加深对模型的理解，树立模型意识，提升数学观察能力.

2.3 典例精晰，运用模型

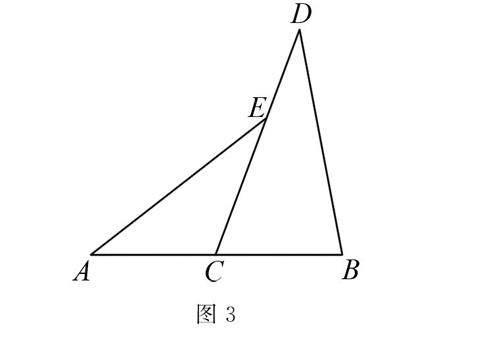
例题 已知，如图3，C是AB的中点，点E在CD上，且∠AEC=∠D.

求证 AE=BD.

问题1 如何证明结论？全等三角形的性质可以吗？等腰三角形的性质可以吗？如何转化条件？

问题2 如何添加辅助线？如图4，延长DC至点F，使得DC=CF，联结AF还是BF？还是都可以？

问题3 还可以添加别的辅助线吗？如图5，延长EC可以吗？

设计意图 通过典型例题的分析引导学生进一步体悟图形运动思想，当题目中出现“中点”时可以联想到需要“倍长中线”，建立8字型全等三角形模型.同时引导学生分析“延长DC至点F，使得DC=CF，联结AF还是BF？”，当联结BF时，无法构造8字型全等三角形，也无法转移边和角，从而是错误的辅助线.另外，引导学生一题多解，从不同的角度思考问题，如果辅助线是“延长EC至点F，使得EC = CF，则应该联结BF”.

2.4 变式练习，巩固模型

练习 已知，如图6，C是AB的中点，点E在CD上，延长AE交BD于点G，联结AD，且DG=EG.

求证 AE=BD.

问题1 如何添加辅助线？

问题2 延长DC至点F，使得DC=CF，联结AF还是BF？还是都可以？

问题3 还可以添加别的辅助线吗？延长EC可以吗？

设计意图 变式练习是在例题的基础上改编而成，引导学生从复杂图形中识别出基本模型.进一步巩固通过“倍长中线”构建8字型全等模型，体会图形的运动可以转移边和角.通过分析辅助线的联结，培养学生数学思维，提升数学语言表达能力，培养学生核心素养.

2.5 畅谈收获，总结模型

请同学们谈谈自己的收获，尝试从“倍长中线”的概念、目的、模型、口诀、思想等方面进行总结.教师引导学生理解“倍：加倍—边等；长：延长—对顶角；中线：边等”，牢记“遇中线，想倍长；构全等，找关系”的口诀.

设计意图 学生通过总结加深对“倍长中线”模型的理解，进一步体悟图形的运动思想，培养学生的数学观察能力、逻辑推理能力以及数学语言表达能力，提升数学核心素养.

2.6 分层作业，内化模型

基础训练 必做题

（1）已知，如图7，在△ABC中，AB = 4，AC = 3，AD是BC的中线，则AD的取值范围为.

能力提升 选做题

（2）已知，如图8，CB、CD分别是钝角△AEC和锐角△ABC的中线，且AC = AB.

求证：CE = 2CD.

拓展提高 选做题

（3）已知，如图9，AD是△ABC的中线，点E、F分别在AB、AC上，且DE⊥DF，

求证：BE+CF＞EF.

设计意图 分层作业主要是兼顾不同层次学生的实际需求，针对性地调控作业难度，促进每个孩子能在原有基础上有所进步.

3 教学启示

3.1 创设问题情境，体悟图形运动

本节课是以沪教版八年级第一学期课本97页第11题作为问题情境，首先分析在已有的图形中能否借助已知条件解决问题.其次，进一步思考如何转化条件从而解决问题.最后，教师引导学生借助图形的运动改变图形的位置，达到转移边和角的目的.在这个过程中，学生可以感悟到图形的运动在几何说理过程中的重要性.

3.2 學生自主思考，构建几何模型

本节课通过典型例题的分析，找到题目中的题眼“中点”，由此联想到“倍长中线”辅助线，构造8字型全等三角形.此题难点是倍长EC或DC之后是与A联结还是与B联结，学生自主思考分析，选择联结哪个点可以有效转化条件，从而进行突破.在这个过程中，不仅培养学生的识图能力，而且锻炼学生的思维，提升模型意识和数学素养.

3.3注重变式练习，强化模型应用

变式训练有助于学生更好地理解和掌握模型，培养学生在复杂图形中抽象出数学模型的能力.本节课的变式练习是在典型例题的基础上改编而成，联结了AD，且延长AE交BD于点G.这道题目相比例题的图形更加复杂，需要学生先识别出基础模型，添加恰当的辅助线，在添加辅助线的时候同样需要考虑联结哪个端点可以有效转化条件.通过这道变式训练，不仅可以检测本节课教学目标的达成程度，同时进一步加强学生对“倍长中线”模型的理解，再次体会图形运动思想，强化模型应用能力.

3.4 发展识图技能，提升核心素养

本节课问题引入、典例精晰、变式练习都紧扣主题，选取了具有代表性的题目.通过层层分析，引导学生归纳总结在何种情况下考虑“倍长中线”，“倍长中线”具体的方法以及“倍长中线”之后联结哪个端点合适等.在这个过程中引导学生识图、标图，发展数学观察能力，提升数学思维能力以及数学语言的表达能力.

参考文献：

[1]吴刚平，安桂清，周文叶.新方案·新课标·新征程：《义务教育课程方案和课程标准（2022 年版）》 研读[M].华东师范大学出版社，2022.

[2]郑兴民.初中数学几何模型的教学误区与解决路径[J].福建教育学院学报，2022，23（09）：30-32.

[3]陈建.“双减”下的初中数学建模思想训练探究[J].福建教育学院学报，2022，23（06）：6-8.

[4]李洪明.如何有效开展初中数学几何教学[J].科学大众（科学教育），2019，（05）：14.