口算算法和算理切勿混淆

顾志能

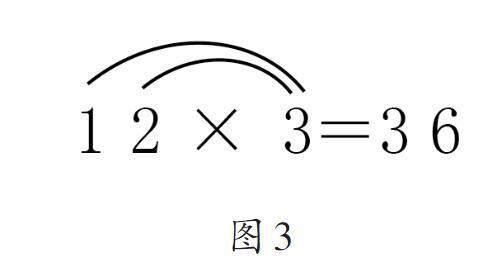
笔者近期连听了几节口算课，发现多位授课教师对口算算法和算理的认识不清晰，导致教学的设计及实施出现明显问题。为此，笔者结合具体课例，对口算中的算法和算理作一些详细说明，期待能引起一线教师的思考。

一

算法，即计算的方法，也就是怎么算。

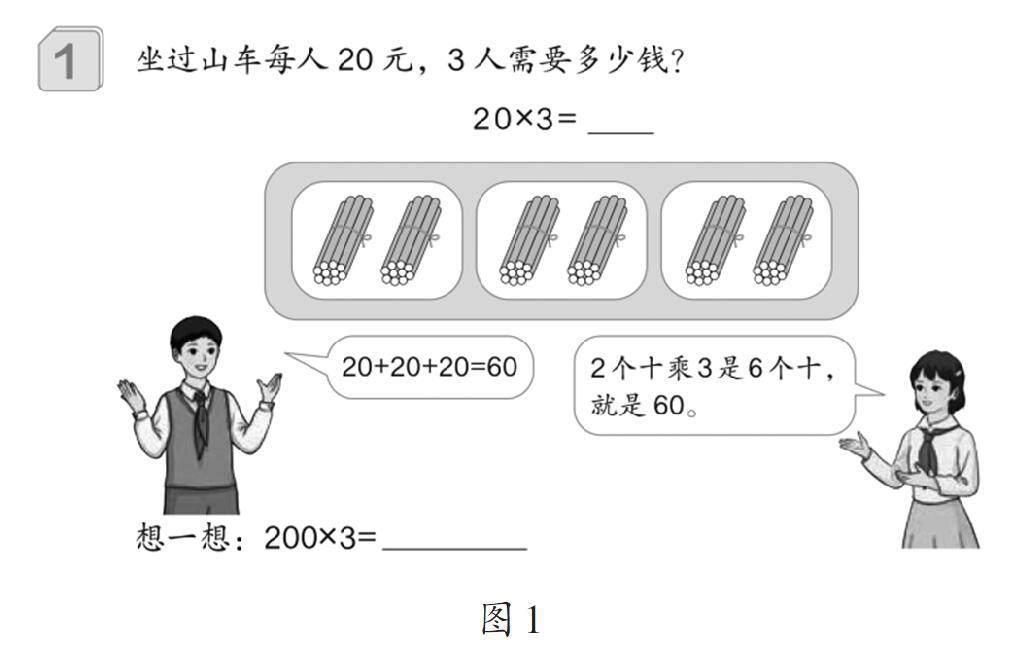
以人教版教材三年级上册的《口算乘法》为例。例1（如图1）中，20×3可以怎么算？“20后面的0先不看，2乘3等于6，6后面再添个0，等于60。”这就是学生心目中这道题最典型的算法。当然，20×3还有另一种算法，即用20＋20＋20来计算，等于60。

算理，即算法背后的道理，也就是为什么可以这样算。

以前述“0先不看，乘后再添0”的算法为例。它背后的道理是什么？20后面的0不看，就只看到了2；这个2是2个十的2，2个十的2乘3，得到6；但这个6是6个十的6，所以还要在6后面添个0，得到结果为60。这就是该种算法的算理。

上述算理，其本质是数的意义和乘法的本质（计数单位不变，计数单位的个数增加）。当然，算理还涉及乘法运算律，如“2个十”乘3变成“2×3”个十，用到了乘法交换律和结合律（这些运算律知识尚未学过，学生依据直观和经验接受即可，下文同）。

至于20×3的另一种算法20＋20＋20，其算理一目了然——乘法的意义，即乘法是求几个相同加数的和的简便运算。

由此可见，算法和算理是计算教学中两个不同的概念，教师教学时需要区分清楚，不可混为一谈。

二

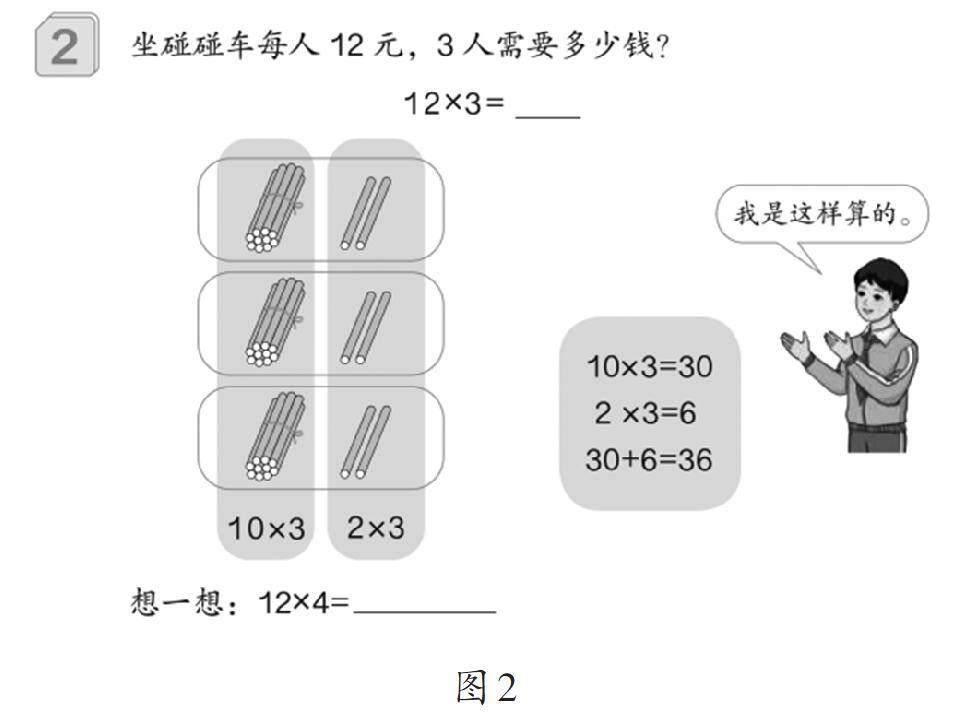
例2（如图2）中的算法与算理更值得一说。

12×3的算法是怎样的？（读者不妨先自己想一想）

用加法来计算，12＋12＋12肯定可行。

用乘法来算呢？很多教师可能会觉得，教材上所呈现的“10×3＝30，2×3＝6，30＋6＝36”不就是算法吗？因此常会有教师直接把这一过程写下来（或让学生写下来），指出这就是这道题目的计算方法。

然而，口算的算法并不需要那么复杂。在学生看来，这道题的口算算法很简单。先用十位上的1乘3得3，答案处先写3；再用个位上的2乘3得6，6写在3的后面；3和6“合起来”就是36。整个算法过程如图3所示（图中的连线，只是学生表达算法或教师引导理解时的辅助记号，实际口算时不用画出来）。

此外还要说明两点：其一，口算的结果是口述的，并不一定要写下来；其二，此题也可以从个位算起，且这是后一节课的优化方向。

那么，这道题这么算，算理是什么呢？

一是数的意义，12就是10与2的和；二是乘法分配律，12×3也可视为10×3加上2×3；三是数的组成，十位上写3，个位上写6，就是30＋6。例题图中小棒的圈画或那三个算式就是在说明这些道理。

因此，小棒的圈画和三个算式都是12×3乘法口算的算理，它们的本质是一样的，只不过前者为直观图式，后者为数学表达。

可能会有教师心生疑惑，教材上的插图明明写了“我是这样算的”，这难道不是算法吗？笔者认为，这是算法过程“完整的、严谨的文字描述”，学生可以如此边口述边写出（想到）答案，但却不需要形式化地写出来，只要在头脑中想到即可。从这个角度来说，教材上的“我是这样算的”改成“我是这样想的”也许更合适。

三

以上所讲的算理算法，在笔者听到的课中，很多教师都是混淆的。最常见的场景是给出小棒情境图，引导学生列式12×3（此时很多学生会直接报出答案36），然后给学生布置一个探究任务（如图4）。

学生探究后，教师组织教学反馈，学生有用连加计算进行说明的，有用圈画小棒图配上三个横式进行说明的，教师引导学生理解，最后确认方法及答案。

画一画或写一写，说明12×3可以怎么算？

上述教学过程存在的问题是显而易见的——算理算法混在了一起，有的学生是在写算法，有的学生是在写算理，或者兼而有之。

针对这样的问题，教学该如何调整？笔者在《理法更分明，教学更合理》一文中已有阐述（详见本刊2023年第10期），即针对这类算法较为简单、学生普遍都会的计算课（特别是口算内容），均可采用“先算法，后算理”的教学思路。在《义务教育数学课程标准（2022年版）》强调数学思维主要是指运算能力和推理意识的背景下，这一教法的意义是明显的，它放大了算理理解的过程，凸显了思维训练的目标。

四

综上所述，口算的算法跟笔算的算法一样，就是一个操作程序，但这个程序相對比较简单，往往可以用很朴素、直白的语言予以概括，如“0先不看，乘后再添0”“先乘个位的数，再乘十位的数”等。运用这个程序就能很直接地得出答案，而不需要再写出“想”的过程。这也就符合了口算的本意——凡是耳听题目口答结果或是看着题目说出结果的计算方法就叫口算，所以口算也叫“心算”或“暗算”。

口算在第一、二学段有很多教学内容，这些内容看似易教易学，但细细思考，这样的内容其实并不好教，里面有很多值得研究的元素。教师在教学时，应厘清其中的算法和算理，然后设计出科学合理的教学过程，引导学生熟练掌握算法，深刻理解算理。

（浙江省杭州市滨江区教育研究院）