基本模型：指向乘法数量关系的一致性

杨春晓 李国强

【摘   要】数量关系教学中存在“关注问题具体特征，忽视量与量之间内在关联”的问题，这一认知局限主要源于对“数量关系一致性”的关注不足。因此，对于乘法数量关系的教学，教师应聚焦一致性，在分析问题、探讨价值的基础上，以基本模型为抓手开展教学。实施中可采用以下策略：低段教学聚焦“每份数”，夯实认知起点；线段表达，凸显乘法的内在联系；融合多元，构建统一模型；拓展应用，彰显模型价值。

【关键词】乘法数量关系；基本模型；一致性

《义务教育数学课程标准（2022年版）》将“数量关系”列为小学阶段“数与代数”领域的主题之一，要求“学生经历在具体情境中运用数量关系解决问题的过程，感悟加法模型和乘法模型的意义，提高发现和提出问题、分析和解决问题的能力，形成模型意识和初步的应用意识”。小学阶段的数量关系主要有加法关系与乘法关系。本文聚焦乘法数量关系的一致性，旨在加深学生对乘法数量关系本质的理解，以优化学生的认知结构，提高其学习效果。

一、问题聚焦：对乘法数量关系教学现状的反思

在教学人教版教材六年级上册“总复习”中的一道题目（如图1）时，笔者让学生观察这道题所给出的条件，写一写有什么发现。结果学生的回答大多集中于题目的外在形式，如“书原价30元，实际降价10%”“付钱数的50%”“付钱数的[13]”“付钱数的1.5倍”等。而当笔者提醒学生看看这几个条件之间有什么共同点时，他们大多也只能回答“都是购物情境”，很少会关注到情境背后隐含的共同的数量关系。不仅如此，许多教师对数量关系的理解也停留在较浅的层面。他们出现这一认知局限的主要原因，与缺乏对“数量关系的一致性”的认识有关。因此，有必要对“数量关系的一致性”进行深入探讨。

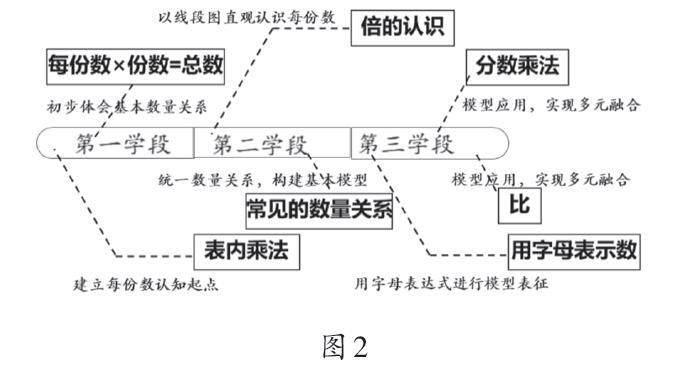
二、价值探寻：乘法数量关系一致性的教学重心

回顾小学三个学段乘法数量关系的教学（如图2），可以发现，在运用乘法数量关系解决问题时，会遇到不同的事件、不同的情境和不同的表述方式，它们的关系纷繁复杂，容易使学生产生困惑。那么，在这些看似不同的问题背后，是否存在某种相同的本质？是否存在一个“万变不离其宗”的核心概念？

从本质上看，乘法是“求几个（份数）相同加数（每份数）的和（总数）的简便运算”。因此，“每份数×份数=总数”是乘法数量关系的基本模型。对基本模型进行深入挖掘与分析，有助于揭示乘法数量关系的一致性，这对学生理解与分析问题至关重要。其主要价值体现在以下几个方面。

（一）结构支撑，理解基本模型从具象到抽象的演变过程

数量关系是数学模型的具体表达形式，是模型思想的基础。教师要引导学生深入探究多种具象的乘法数量关系，结合不同数量关系之间的逻辑联系，以形式化的基本模型进行表达。“每份数×份数=总数”这一基本模型，有助于学生构建数量关系之间的逻辑联系，感受不同知识的深刻内涵，从而加深对知识结构的理解，提高学习效果。

（二）层层递进，感悟基本模型化繁为简的价值

基于乘法数量关系的一致性，关联已学的整数、小数、用字母表示数、分数的数量关系等知识，将原本分散在不同年级、不同领域的不同事件、不同情境、不同具体关系进行化归。例如，与购物相关的问题可以统一为“单价×数量=总价”，与行程相关的问题可以统一为“速度×时间=路程”，进而把乘法数量关系归纳为与个数有关的问题和与物理量有关的问题。在此基础上，各种具体问题层层递进，最后都归结为“每份数×份数=总数”这一基本数量关系。这种化繁为简的做法，不仅让学生感受到基本模型的特殊魅力，增强学习兴趣，减轻学习负担，还有助于学生养成追根求源的深度学习习惯。

（三）整体把握，建立研究對象从局部到整体的本质联系

在“每份数×份数＝总数”这一基本模型中，每个量可以是整数、小数、分数，甚至可以是字母。这使得乘法数量关系的研究对象从整数扩展到小数、分数以及用字母表示的数，涵盖“数与代数”整个领域，甚至涉及小学数学的全部内容。乘法数量关系的基本模型从局部到整体建立起研究对象间的本质联系，有助于学生体会和理解教学内容的多样性与本质的一致性，促进学生对数学学习内容的整体把握与深度理解。

三、实践探索：乘法数量关系的教学策略

如前所述，关于乘法数量关系的题目众多，问题千变万化。因此，基本模型对学生数学学习有着非常重要的作用。那么，如何利用基本模型更好地开展乘法数量关系的教学呢？具体有以下几种教学策略。

（一）低段教学聚焦“每份数”，夯实认知起点

学生低年级时学习的“每份数”概念，是他们理解数量关系的基础，更是他们初步建立数量关系的关键。教师应将“每份数”作为教学重点，并引导学生对其进行精准识别与理解。为了实现这一目标，教师需要精心策划一系列“种子课”，系统性地推进整体教学。下面以“表内乘法”为例，探讨如何让学生深刻体验每份数的意义。

【教学片段1】“表内乘法”教学

教师出示图3。

师：你们看到了什么？

生：图中有4个长方形，每个长方形中有3个圆。

师：那么一共有几个圆呢？

生：一共有12个圆。

师：你是怎么知道的？

生：每个长方形中有3个圆，有4个这样的长方形，3+3+3+3=12或3×4=12。

师：那如果有4个铅笔盒，每个铅笔盒里装有3支铅笔，一共有几支铅笔？这个问题谁会解决？

生：这个问题不就对应刚才的图吗？黑板上的圆就是铅笔，长方形就是铅笔盒。

通过聚焦问题中的“每份数”，学生不仅理解了如何通过加法3+3+3+3得出总数，还掌握了如何通过乘法3×4更简洁地得到答案。这种教学方法有助于学生巩固对乘法概念的理解，更重要的是，能使学生对“每份数”有更深入的认识，为他们后续进一步学习乘法数量关系奠定坚实基础。

（二）线段表达，凸显乘法的内在联系

线段图将抽象的数量关系转化为具象的线段表达，使得数量关系形象化。学生可据此直观地感知每一份的数量及其与份数之间的关系，更好地理解数量之间的内在联系。

【教学片段2】“倍的认识”教学

教师出示问题：已知柳树有30棵，松树数量是柳树的4倍，松树有多少棵？在教师的引导下，学生画出了如下线段图（如图4）。

师：观察示意图，说一说谁是谁的几倍。

生：松树的数量是柳树的4倍。

师：刚才我们将谁视为1份？

生：柳树的数量（上面的一小段）。

师：以30棵柳树为1份，像这样的1份我们叫作每份数。松树的数量就是4个这样的每份数，即30×4=120（棵）。

引入线段图，有助于加深学生对基本模型的理解。通过线段图，学生可以直观地感受到每份数在解题过程中的重要性。此外，教师还要引导学生运用不同的每份数来应对相同的问题，以帮助学生深入理解数量关系的本质。

【教学片段3】“除数是一位数的除法”教学

教师出示问题：买2本故事书30元，要买4本这样的故事书，需要多少钱？让学生独立思考后汇报想法。

生（指着自己画的图5）：先求出1本故事书的价格是15元，再求出买4本故事书需要60元，即30÷2×4=60（元）。

师：还有别的方法吗？

生：4是2的2倍，因此4本故事书的价格也是2本故事书价格的2倍，即4÷2×30=60（元）。

师：这两种计算方法有什么不一样？

生：第一种方法是将1本故事书的价格看作每份数，第二种方法是将2本故事书的价格看作每份数。

师：为什么选的每份数不一样，结果却是一样的？

生：将1本故事书的价格看作每份数时，总价里面包含4个这样的每份数；将2本故事书的价格看作每份数时，总价里面包含2个这样的每份数。因此，两种计算方法的结果相同。

学生借助直观的线段图，认识到乘法数量关系实则是多个每份数的累加，进而明确每份数至关重要，了解数量的内在联系，加深对数量关系的理解，提高解决问题的能力。

（三）融合多元，构建统一模型

在小学数学教学中，模型意识具有举足轻重的作用。为了使学生能够更加深入、准确地理解和把握数量之间的关系，笔者试图将在原来实际运用中提炼的多个数量关系建立有机的联系，形成一个内容完整、结构清晰的基本模型，通过基本模型加深学生对乘法数量关系本质的理解。

【教学片段4】“乘法数量关系模型”教学

教师出示要解决的问题，让学生独立思考后汇报想法。

问题1：每个不粘锅的售价是105元，购买4个这样的不粘锅一共多少钱？

问题2：汽车每小时行驶75千米，4小时可以行驶多少千米？

生：根据数量关系“单价×数量=总价”，第1题答案为105×4=420（元）。

生：根据数量关系“速度×时间=路程”，第2题答案为75×4=300（千米）。

师：从这两个问题中，你们发现了什么？

生：我发现它们用到的数量关系其实是一回事。

师：你能再说得具体一些吗？

生：单价和速度都可以看作每份数，数量和行驶时间都可以看作份数，总价和路程则是总数。因此，两道题都可以用“每份数×份数=总数”来表示。

师：对！这就是我们之前提到的乘法数量关系的基本模型。利用这个模型，能帮助我们快速地解决各类乘除法的问题。

“每份数×份数=总数”这一基本模型不仅简化了数学题的类型，而且勾连了所学知识，使学生能够更加直观地理解数量之间的内在联系。此外，它还为学生提供了一个高效且简洁的解题框架，帮助他们快速洞察问题的本质，捕捉关键信息，找到解决问题的有效路径。

（四）拓展应用，彰显模型价值

在不同的学习阶段，学生的认知发展水平存在差异，乘法数量关系模型的表现形式也会有所变化。因此，学生学习过程中的侧重点也会有所不同。倍数、分数和比都是描述数量关系的具体方式，它们在小学的不同学段都有涉及，但各自的内涵和重点有所不同。分数的独特性使其在教学中占据重要地位，因此，教师教学时要引导学生理解分数（分率）在乘法数量关系中的角色，使他们认识到每份数和份数也可以是分数，尤其是份数还可以是非整数。教师通过这样的引导，拓展与深化乘法数量关系基本模型的应用，全面体现其教学价值。

【教学片段5】“分数乘法”教学

教师出示问题：一桶水6升，[13]桶水多少升？让学生独立思考后汇报想法。

生：6÷3=2（升）。

师：你是怎么想的？

生：我把[13]桶当作每份数，因为总数是6升，6升中有3个这样的每份数，因此可以用6÷3来解决。

师：还能怎么列式？

生：我认为还可以用6×[13]来解决。

师：你能用学过的基本模型来解释吗？

生：我把一桶水6升看作每份数，那么份数就是[13]桶，所以我是根据“每份数×份数=总数”来列式的。

师：这样解决有什么不一样？

生：[13]桶的单位“1”是1桶，此时每份数是1桶，份数小于1，所以总数就比每份数小了。

通过分析少于1桶和几桶都可以代表份数，学生认识到倍数、分率和比都可用于描述两个量之间的关系，并在实际应用中实现了这些概念的统一。将基本模型从整数拓展到分数和比，不仅拓展了基本模型的应用价值，更为学生全面深刻地认识数量关系提供了抓手和机会。

四、实践反思：乘法数量关系概念本质的一致性教学反思

（一）明确目标，系统把握

在小学阶段，学生对乘法数量关系的理解是一个循序渐进的过程。从简单的“每份数×份数=总数”“1倍数×倍数=总数”到“单价×数量=总价”“速度×时间=路程”，再到“单位‘1的量×分率=对应量”等数量关系，他们逐步建立起对乘法数量关系的系统认识。这些数量关系看似不同，实则相通，都可以归于基本模型“每份数×份数=总数”。学生在感悟乘法数量关系的一致性的过程中，深入理解各个部分是如何相互关联、相互影响的，这对提升他们的数学思维和解题能力具有重要意义。

（二）重视直观，凸显结构

在小学数学中，直观图对于助力学生理解乘法数量关系、感悟乘法数量关系的一致性具有显著效果。通过长方形图式、线段图，学生能更清晰地看到数量关系的内在结构，并对其进行深入理解。这些直观图式不仅能激发学生的学习兴趣，还能帮助其形成系统、清晰的数学思维，为后续学习奠定坚实基础。

（三）广泛联系，整体建构

学生在学习乘法数量关系时，容易受到数类型的不同的影响，从而忽视了它们之间的整体性和关联性。因此，教师在设计教学时，应精心构思，紧扣核心内容，分析知识之间的逻辑关系，旨在利用学生的已有认知，通过图形、模型等多维度教学手段，帮助学生逐步建立起富有整体性、逻辑性的知识体系，凸显乘法数量关系的一致性，加深学生对数量关系本质的理解。

参考文献：

［1］中华人民共和国教育部.义务教育数学课程标准（2022年版）［M］.北京：北京师范大学出版社，2022.

［2］商红领.内外贯通 探本求源 感悟一致性：“整数、小数、分数的一致性”教学实践与思考［J］.小学教学（数学版），2022（3）：66-69，3.

［3］王玉彬，姚颖.探索运算本质 构建运算联系：数的运算“一致性”的探索实践与研究［J］.小学数学教育，2022（9）：26-27.

［4］汪松浩.从倍比关系看分数类解决问题的教学［J］.教学与管理，2017（14）：42-44.

（1.杭州師范大学附属乍浦实验学校2.杭州师范大学中国教育现代化研究院）