基于问题解决的初中数学深度学习促进策略

陈鑫海

摘 要：深度学习是培养学生掌握核心学术内容、批判性思维与问题解决能力、有效沟通与合作、自我导向学习等能力的必经过程，是培养学生应对未来社会挑战关键能力的必经路径。基于学生初中数学学习的现状，以人教版七年级下册“8.2 消元——解二元一次方程组”第二课时教学为例，探讨促进学生深度学习的有效策略，可以总结出做法：创设真实问题情境，通过强化主动理解，可以有效发展学生的批判性思维；设计问题描述活动，通过强化思维整理，可以有效促进学生的新知建构；设计问题探讨活动，通过强化知识深层加工，可以有效重构学生的认知体系；设计问题分析活动，通过感悟数学学科本质和基本思想，可以促进学生的知识迁移；设计解决问题活动，通过建构问题解决模型，可以促进学生形成解决问题能力；设计回顾与反思活动，通过搭建反思支架，可以促进学生形成评价与反思能力。

关键词：初中数学；问题解决；深度学习；活动设计；六维能力

中图分类号：G63 文献标识码：A 文章编号：0450-9889（2024）07-0077-06

结合当前义务教育质量监测结果可知，当前初中数学课堂教学依然存在一些亟待解决的难点问题，如教师对课堂教学缺乏有效调控，学生在课堂中依然处于机械、被动的浅层学习状态，师生缺乏对教学过程的有效反思，等等。史宁中教授把学生缺乏根据情况预测结果和根据结果探究成因的能力作为数学教育的短板，要求教师在解决问题教学中重视培养学生“一头一尾”的能力，“一头”即发现和提出问题的能力，“一尾”即学习过程中的评价与解决问题后的反思能力。在笔者看来，深度学习是提升学生这“一头一尾”能力的有效路径。

“深度学习”是一个不断演进的概念。最初针对学习的过程展开研究，等同于深层学习，与浅层学习相对；之后逐渐向教学领域延伸，与教师的教关联起来。1976年，瑞典哥德堡大學的两位心理学家弗伦斯·马顿（Ference Marton）、罗杰·萨尔乔（Roger Saljo）在《学习的本质区别：结果与过程》一文中首次提出表层学习与深层学习的概念，认为学生在学习过程中采用不同的学习方式会产生不同的学习结果，深层学习主要以联系和理解为主要特征，而浅层学习以机械记忆重复和孤立的信息为主要特征。1987年，澳大利亚学者约翰·比格斯（John Biggs）在其专著《卓越的大学教学：建构教与学的一致性》中强调了深度学习与教师教学之间的关联，认为深度学习是学习者个体与教学环境进行交互的方式。2000年，诺埃尔·恩特威斯尔（Noel Entwistle）在《通过教学和评估促进深度学习：概念框架和教育背景》一文中通过对大学生学习过程的访谈调研，认为深度学习是一种以理解意义为目的的主动学习方式，包含联系观点、寻找模型和原则、使用证据、检查论证的逻辑性和正确性等特征；浅层学习则主要采用死记硬背的学习方式。直至2011年美国的威廉和弗洛拉·休利特基金会发起了一项由美国研究学会（AIR）组织实施的深度学习SDL项目（Study of Deeper Learning： Opportunities and Outcomes），2012年美国国家研究院（NRC）发布了一个《为了生活和工作的教育：在21世纪发展可迁移的知识和技能》（Education for Life and Word：Developing Transferable Knowledge and Skill in the 21st  Century）的研究报告，“深度学习（Deep Learning）”的概念才得以正式确立，开始与21世纪技能即掌握核心学术内容、批判性思维与问题解决能力、有效沟通、合作、自我导向学习、学习心态这六维能力相互融通［1］。

无论以上研究者如何论述深度学习，但将深度学习的目标定位于使学生牢牢掌握、深刻理解更深层次的知识，并将自己的知识与技能运用到学校内外的任务和环境中，是大家一致认可的。这样的深度学习，与数学教育有极大的内在关联，更加强调学习的现实意义，更加有利于培养学生“会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界”［2］11的“三会”核心素养，从而顺利提高学生在数学问题解决过程中那“一头一尾”的能力。为此，《义务教育数学课程标准（2022年版）》要求教师注重发挥情境设计与问题提出对学生主动参与教学活动的促进作用，基于真实情境，提出能够引发学生思考的数学问题或引导学生提出合理问题，让学生经历数学观察、数学思考、数学表达、概括归纳、迁移运用等［2］87深度学习的过程，从而逐渐提高学生“一头一尾”的能力。下面笔者以人教版七年级下册“8.2 消元——解二元一次方程组”第二课时教学为例，探讨基于问题解决的初中数学深度学习促进策略。

一、创设真实问题情境，通过强化主动理解，有效发展学生的批判性思维

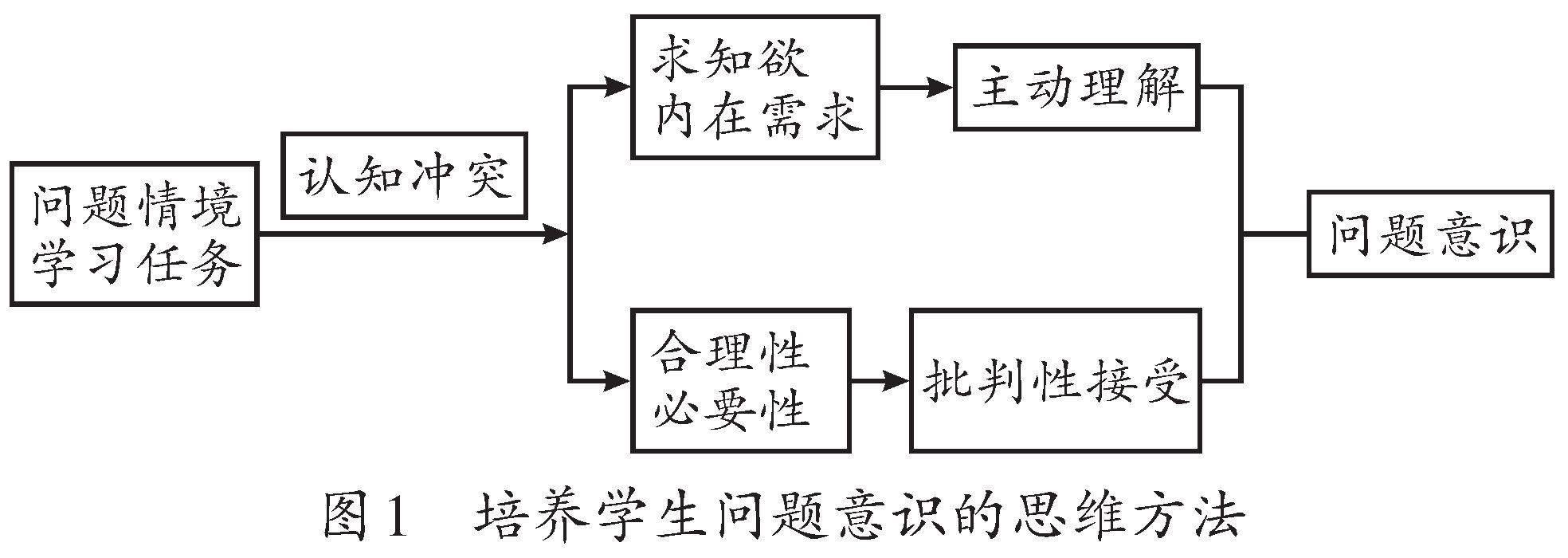
批判性思维作为一个技能的概念可追溯到杜威的“反省性思维”，即“能动、持续和细致地思考任何信念或被假定的知识形式，洞悉支持它的理由以及它所进一步指向的结论”［3］。学科教学中，将批判性思维和问题解决能力相提并论，则是指运用某一学科的核心工具和技术阐释和解决问题的能力。初中数学教学中，为了培养学生的批判性思维和问题解决能力，教师应努力创设真实的有挑战性和吸引力的问题情境或学习任务（如图1），激活学生已有的认知经验：当学生发现无法用旧知识解决新的问题或者情境中的问题与自己已有的认知存在些许差异时，认知冲突随之产生。此时此刻，正是教学的“不愤不启”之时，教师适时介入，引导学生经历主动理解、集体讨论和批判性接受的思维发展过程，可有效促进学生的深度学习，培养学生的问题意识，发展学生的数学认知。

教学实践中，问题情境或学习任务的创设，必须建立在学生已有的认知经验之上，以利于学生形成强烈的问题意识和积极的主动思维，从情境中去感知现象与其本质规律之间的矛盾冲突，从而理解数学学习的意义和价值。例如，在“8.2 消元——解二元一次方程组”第二课时中，教材首先呈现了一道思考题，即上一课时用代入法求解的一个方程组（如图2），引导学生通过观察两个方程中同一个未知数y的系数相等这一特殊关系，发现为方程组求解的新方法。这样的问题编排，其实已经为学生提示了一种发现数学知识产生过程的新思路。

然而深入分析学生的学习过程，可以发现以下问题：直接引导学生观察两个方程中未知数y的系数相等这种特殊关系，虽然能够让学生快速感知到一种新的问题解决方法，但这样的感知过程却是单薄的，思维发展的层次较低，不能有效激活学生已有的认知经验，不利于诱发学生积极、主动的思考，不利于发展学生的批判性思维与批判性接受新知识的能力。为此，笔者变更了以上问题的呈现方式，先创设了一个真实的有挑战性和吸引力的问题情境（如下页图3“问题1”中提到的两种问题呈现方式），触发学生已有的认知经验，引导学生自主感知知识产生和发展的过程；再回归教材所提供的方程组（如下页图3中的“问题2”），让学生运用从“问题1”中习得的方法，去自主理解和解决“问题2”中的问题，从而有效促进学生的主动理解和批判性思维的发展。

二、设计问题描述活动，通过强化思维整理，有效促进学生的新知建构

在课堂教学中，促进学生展开深度学习，关键在于设计有效的深度学习活动，激活学生的原认知，引导学生经历同化与顺应的学习过程，在新认知与原认知之间建立起有效的“联结点”，通过归纳概括新知识而获得新知识的意义，同时将新知识纳入已有的知识结构，从而建构起新的认知体系［4］。同化和顺应是瑞士心理学家皮亚杰在其儿童认知发展阶段理论中提出的两个重要概念，用来描述个体适应环境的机能：同化是指把外部环境中的有关信息吸收进来并结合到儿童已有的认知结构当中的一种学习过程；顺应则是指外部环境发生变化，而原有认知结构无法同化新环境所提供的信息时所引起的儿童认知结构发生重组与改造的过程，即个体的认知结构因外部刺激的影响而发生改变的过程。

在课堂教学中，遵循如图4所示的思维逻辑，教师可通过设计问题描述学习活动，引导学生经历数学观察、数学思考、数学表达、概括归纳的深度学习过程，首先让学生对课堂中所发现的问题或所遇到的难以理解的现象进行客观的感官描述，理清问题所在，然后让学生集中思维目标，经历比较、概括等思维整理过程，從而清晰地界定自己的困惑或判断，以此推动学生对问题的理解与发现，使学生获得知识的本质属性或一般性结论，顺利建构新知，提高数学表达能力。

例如，在“8.2 消元——解二元一次方程组”第二课时中，教师可基于前面的两个问题，提出问题3和问题4（如图5）。通过问题3，可引出方程组的三种解法，让学生围绕方程组的特征进行描述、判断，叙述选择方程组解法的缘由。学生通过观察、比较，可以做出一般性的归纳概括，如：因两个方程中都含有相同的项“x+y”，可以运用整体代入法，将方程①整体代入方程②后，便可解出方程组；因方程组两个方程中有一个未知数的系数相同，将两个方程左右两边分别相减，同样可以为方程组求解。在以上问题解决过程中，学生经历了解法展示和问题描述的活动过程，与原有知识经验建立起联系，有效激活了原认知，经历了不同解法的比较、归纳、概括等思维整理与发展过程，从而顺利产生了问题4的“想法”，建构了新的认知：当解含有相同的项或有一个未知数的系数相同的二元一次方程组时，可以运用整体代入法或做减法进行消元，这比直接运用一般的代入消元法更为简便。

三、设计问题探讨活动，通过强化知识深层加工，促进学生重构认知体系

知识深层加工是对相关知识进行系统整合的过程，要求遵循一定的规律，理顺相应的关系，建立知识间的联系，进而重构认知体系［5］。受限于学生的认知能力，初中数学教师创设以问题探讨为主的学习活动，可通过组织学生对“同构问题”和“相似问题”进行问题分析与探讨，使学生学会提炼有用信息和知识重点，厘清问题的构成要素，与更大的概念框架建立联系，以形成结构性较强的知识体系，进而提出有价值的问题（如图6）。

例如，在“8.2 消元——解二元一次方程组”第二课时前面四个问题的基础上，教师可接着提出问题5和问题6（如图7），引导学生对知识进行深层加工，展开问题探讨学习活动。学生通过探讨问题5可发现，与问题2比较，两个方程中不存在可直接整体代入另一个方程的代数式，因此运用之前所学的方法无法直接解决上述问题，但与之相类似的是，这个方程组中存在一个系数刚好互为相反数的未知数，可以运用方程两边相加的方法进行求解。进一步观察，学生很容易发现，问题5与问题2中的两个方程组结构相似、解法相似，进一步抽象概括，可得出如下结论：当方程组中同一个未知数的系数互为相反数或相等时，两边相加或相减，就能消去这个未知数达到消元的目的，进而达成为方程组求解的目的，这便是加减消元法。问题6的提出，旨在引导学生更为系统、全面地思考解方程组的方法。在经历了对“同构问题”和“相似问题”进行问题探讨的过程之后，学生通过提取类似问题的构成要素，与同构问题进行比较，经历更进一步的抽象概括，将所学内容全部有机地联系起来，经历知识整合与深层加工的过程，从而获得了知识的深层意义，形成了更大的概念框架，重构了知识体系。

四、设计问题分析活动，通过感悟数学学科本质和基本思想，促进学生的知识迁移

把握数学基本思想和学科本质，指的是让学生在进行问题解决的过程中通过灵活运用数学基本思想，深入把握数学知识本质，不断提升思维品质和学习力，发展数学思维［6］。问题分析活动需要学生经历对问题进行分解和排序的过程，以形成对问题本质的理解，进而提取和内化知识，确定解决问题的思路和方法，提出解决问题的策略，呈现解决问题的完整过程。如图8所示，分析问题的学习活动设计应首先引导学生将问题进行分解和排序，转化为用已学知识和方法能够解决的问题，从中把握问题的本质，再调用原有数学活动经验和思维方法，针对新的问题提出自己的解决方案，进一步感悟知识的本质内涵及其中所蕴含的数学基本思想，进而形成解决问题的基本策略，促进知识迁移。

课堂教学中的问题分析学习活动设计，应有步骤有策略地展开，以利于学生对问题进行多角度、多层面的结构化分析，促进学生形成问题解决的逻辑结构及解决途径，培养学生的结构化思维。例如，在“8.2 消元——解二元一次方程组”第二课时中，教师先通过呈现例3（如图9），提出了一个新的问题，作为问题分析学习活动的起始，继而提出了问题7和问题8，引导学生有序展开问题分析活动。学生在观察例3中的方程组时很容易发现，这个方程组中的两个方程中不存在未知数系数相同或相反的项，因此不能直接使用加减消元法进行消元，且方程组中含有未知数的项的系数比较复杂，若简单使用代入法，不是不可以，只是运算量较大。学生经过系统思考，最终提出可以采用对方程组进行适当变形的方法加以解决，于是提出了将两个方程转化为未知数系数相同或相反的项的两种方案，一种是将两个方程中未知数x的系数都转化为15，另一种是将未知数y的系数分别转化为12和-12，再运用加减消元法来解决问题。

在以上学习过程中，学生通过问题分析，发现所给方程组中不存在同一个未知数系数相同或相反的项、无法直接使用加减消元法来解方程组，于是进一步感悟“消元”的知识本质、感悟其中的转化思想——将二元一次方程组转化为一元一次方程，从而提出了两种问题解决方案，形成了解决问题的基本策略。

五、设计解决问题活动，通过建构问题解决模型，促进学生形成解决问题的能力

设计解决问题活动，旨在让学生在类似的情境中，将逐渐完善的知识、经验有效迁移运用到新的情境当中，通过建构问题解决模型，形成稳定的知识经验，进而有效解决新的问题，形成解决问题的关键能力。如图10所示，课堂教学中的解决问题过程是学生通过独立思考，迁移运用已学知识，并选择合理化的解决方案或相应的策略、模型，经过实践操作解决问题的过程，同时也是将数学知识进行提炼和优化，将模糊、杂乱的数学思维条理化，以验证、确认问题解决的过程和结果，最终形成问题解决的能力和思维模型的过程。独立思考和自主操作，为的是明晰知识间的逻辑联系，辅助梳理解决问题的途径，通过经历以上高阶思维发展的过程，最终形成解决问题的相应策略或模型，并从经历知识有效迁移与解决问题的过程中体验到成就感。

例如，在“8.2 消元——解二元一次方程组”第二课时中，教师呈现问题9和问题10（如图11），引导学生展开解决问题活动。为了解决问题9，学生通过独立操作，得出了多种方法。除少部分使用代入法外，大部分学生选择了将两个方程进行适当变形的方法，如先通过“①×3，②×2”或“①×5，②×3”对两个方程进行变形，再运用加减消元法解方程组。在完成解决问题的过程以后，学生进行了交流探讨，发现在这个问题情境中，运用加减消元法消去未知数x比消去未知数y的运算量要大，由此可以得出结论：消去未知数y解方程组的方案更优。在对问题解决方案进行优化和评价的过程中，学生还可以归纳概括出解决问题的一些一般方法，如：在运用减法消元时，方程组的变形应尽量将未知数的系数转化为它们的最小公倍数，以降低运算量，同时应尽量避免出现系数为负的情况。

六、设计回顾与反思活动，通过搭建反思支架，促进学生形成评价与反思能力

课堂教学中的反思支架，指的是对学生是否完成课堂学习任务或达成学习过程中的变化与发展等所设计的一种促进学生进行自我评价与反思的思维支架，以此培养学生的数学理性以及看待问题的深刻性，引导学生在反思与感悟中经历从基础知识、基本技能到核心素养升华的过程［7］。在笔者看来，要提升学生的数学核心素养，必须培养学生反思、质疑的能力，促进学生养成良好的学习习惯，提升学生的思维品质。如图12所示，课堂教学中，教师所创设的课堂回顾和评价活动，侧重引导学生展开从知识到方法、从方法到技巧、从技巧到数学思想等不