2023年高考数学新课标全国Ⅰ卷压轴题的题源及推广

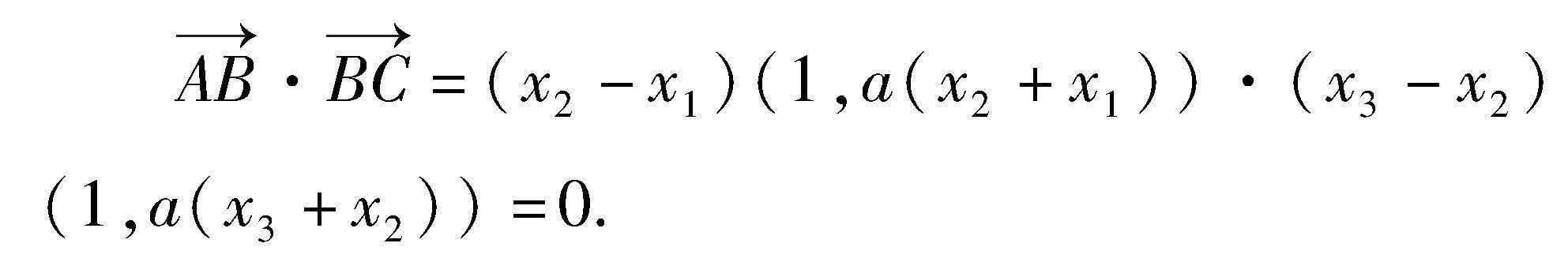
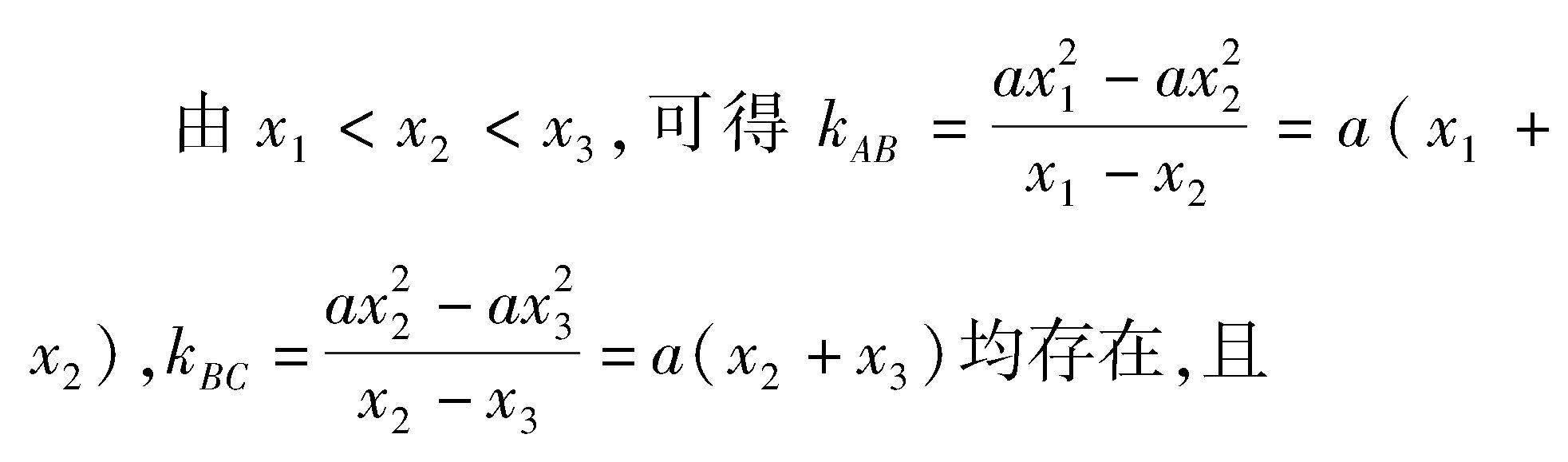
摘 要：文章针对2023年高考数学新课标全国卷压轴题（即第22题）进行了深度探究，旨在帮助广大教师和学生开拓思维，提高数学解题能力.

关键词：高考压轴题；平面解析几何；不等式；推广；编拟习题

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2024）07-0010-05

2023年高考数学新课标全国卷压轴题（即第22题）是一道平面解析几何题，但涉及不等式问题.文章给出了这道题的题源及推广，由得到的推广容易编拟出大量的类似题目.

1 一道高考压轴题

2 高考压轴题的题源

题2 （1998年上海市高中数学竞赛试题第三题）如图1，已知一个正方形的三个顶点A，B，C均在抛物线y=x2上，求该正方形面积的最小值.

解析 如图1所示，可设满足题设的正方形是正方形ABCD，三点A（x1，x21），B（x2，x22），C（x3，x23）（x1

假设x1，x2，x3均是非负数，由AB⊥BC，可得

即（1，x2+x1）·（1，x3+x2）=1+（x2+x1）（x3+x2）=0.

即（x2+x1）（x3+x2）<0.

所以x1，x2，x3不可能均是非负数也不可能均是非正数，即x1，x2，x3中有负数也有正数，因而x1<0

kABkBC=（x1+x2）（x2+x3）=-1<0.

若kAB<0，则kBC>0.

若kAB=x1+x2>0，由x1<0，可得x2>0.

再由x10.总之，kBC>0.

再由弦长公式［1］，可得

由均值不等式及平方平均≥算术平均，可得

k2+1≥2k（当且仅当k=1时取等号），

进而可得当且仅当k=1（即图1中的正方形ABCD的三个顶点A，B，C的坐标分别是（-1，1），（0，0），（1，1））时，正方形ABCD的面积BC2最小，且最小值是2.

3 对题1（2）结论的推广

证明 如图2所示，可设满足题设的矩形是矩形ABCD，三点A（x1，ax21），B（x2，ax22），C（x3，ax23）（x1

假設x1，x2，x3均是非负数，由AB⊥BC，可得

即（1，a（x2+x1））·（1，a（x3+x2））=0=1+

a2（x2+x1）（x3+x2）=0.

即（x2+x1）（x3+x2）<0.

所以x1，x2，x3不可能均是非负数也不可能均是非正数，即x1，x2，x3中有负数也有正数，因而x1<0

kABkBC=a2（x1+x2）（x2+x3）=-1<0.

若kAB<0，则kBC>0；

若kAB=a（x1+x2）>0，由x1<0，可得x2>0.

再由x1

a（x2+x3）>0.总之，kBC>0.

如图2所示，过点B作线段TH∥x轴，且AT⊥

可再设点B（p，ap2）（x1

又由两点A，C均在抛物线y=ax2上，可得

综上所述，可得欲证结论成立.

4 对题1（2）结论的再推广

（2）如图3所示，由题设知可设三点A（x1，ax21），B（x2，ax22），C（x3，ax23）（x1

再由弦长公式，可得

设矩形ABCD的面积是S，由①②，可得

进而可得欲证结论成立.

证明 如图3所示，可设满足题设的矩形是矩形ABCD，且可设三个顶点A（x1，ax21），B（x2，ax22），

C（x3，ax23）（x1

（3）若矩形ABCD的三个顶点A，B，C（它们的横坐标依次增大）均在抛物线y=ax2+bx+c上，且|AB|=463|BC|，则|AB|min=2103|a|，矩形ABCD面积的取值范围是［569a2，+∞）.

5 结束语

通过对高考试题的研究，我们可以更好地理解考试，揭示重点考查内容，从而更有效地引导教学，为高效教学提供数据支持，重视对高考试题的研究，能够精准地捕捉命题趋势，科学地调整教学内容.

参考文献：

［1］ 甘志国.高中数学题典精编（第一辑）：不等式·推理与证明[M].哈尔滨：哈尔滨工业大学出版社，2022.