展折叠之美,育思维之花——2021年深圳中考第15题感悟

⦿ 广东省深圳市龙华区外国语学校教育集团 刘小会

折叠问题是中考数学的高频考点,深圳中考也不例外.折叠问题主要分直接计算型和分类讨论型两大类题型,由浅入深,难度逐渐加大.2021年是深圳新中考第一年,数学试题的难度一度上了热搜.很多学生反映“题目很新”“题目很难”等.具体真相如何?我们一起来揭开填空压轴题的真面目,感受数学之趣、数学之美,提升数学素养.

1 真题呈现

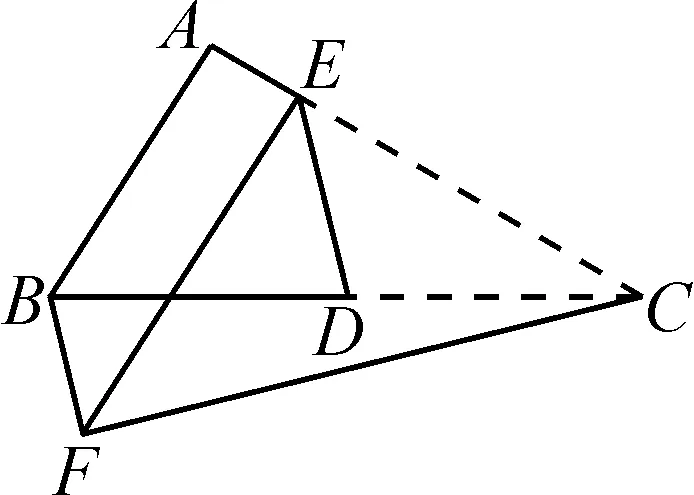
图1

2 试题赏析

纵观深圳近几年中考数学试卷,折叠问题旧瓶装新酒,连续作为选填压轴题.此题作为2021年的填空压轴题,精心设计,巧妙构造.主要体现在:(1)不是单纯的折叠问题,而是通过折叠操作后,结合平行四边形的构造,求解线段长度.(2)已知数据含有根号,防止学生考试时通过测量算出得数.(3)笔者利用几何画板还原题干三角形,发现很难准确画出满足题干条件的三角形,多少都会出现误差.那么,该如何找到满足如此条件的三角形呢?试问,如果改变题干线段长度或者减少已知条件,此题可解吗?笔者也在反思是否是自己才疏学浅,没掌握题干精髓和命题者的意图.一个如此特殊的三角形,进行三角形内部折叠后,同时满足直线平行和存在直角两个条件.我们可以反解这个三角形吗?从题目反观命题者的意图,条件很多,少一个也不行,多一个就成“累赘”.最后,借助几何画板,笔者还原了题干三角形,并且在绘图过程中发现了这道题的变式训练.

3 解法探究

添加辅助线是解决本题的关键所在.本题是折叠问题中的直接计算型.通过证明,挖掘已知条件,直至找到我们熟悉的三角形.对于求解线段长度的题目,如果学生具备线段长度求解的模型意识,就可以突破添加辅助线这一难点.大胆猜测,辅助线水到渠成.再次反观命题者的意图,涵盖折叠所有的性质,角平分线、垂直、平行四边形和等腰三角形等知识点均有涉及.这些都是中考复习中的核心考点,对于考生来说,在考场如何能正确解答此题呢?针对题目,笔者给出4类思路,7种解法.

思路一：添平行之线,连接已知和未知.

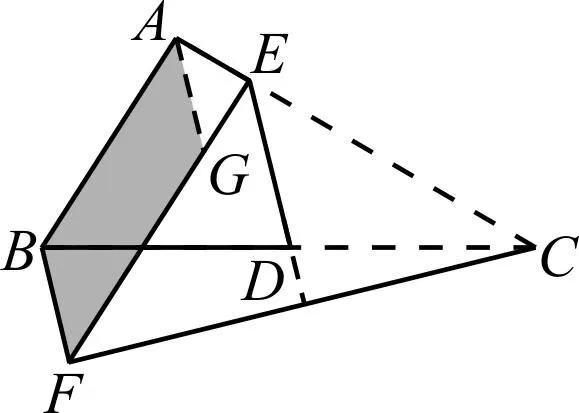
图2

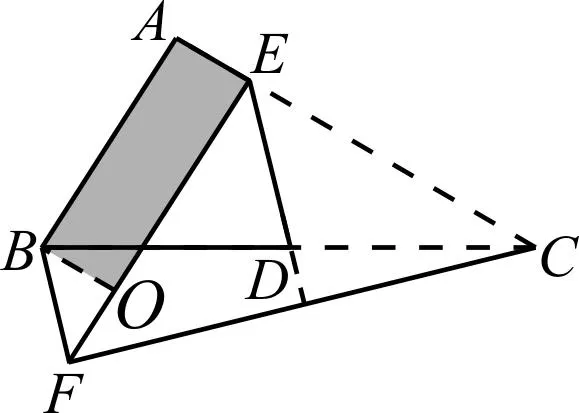
图3

解法3：如图4,过点F作FO∥AE交AB的延长线于点O,构造平行四边形AEFO,接下来类似解法1和解法2,可解.

图4

点评：题目给出AB和EC的长度,求解AE.这三条线段看起来没有联系,怎样把它们联系起来呢?这类问题的一般求解策略为添加辅助线,把未知和已知线段集中到一个三角形中.此方法的突破关键是平行四边形的构造,这是一种比较常规的解法,考生在考场也比较容易想到.此外,针对填空题解题技巧,此题的答案比较容易猜到.几何能力强的考生会先有意识猜测已知线段间的加减关系,然后带着目标去添加辅助线,再结合其余条件,即可写出正确答案.

思路二：延边长之线,挖掘隐藏信息.

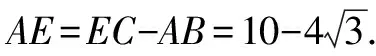
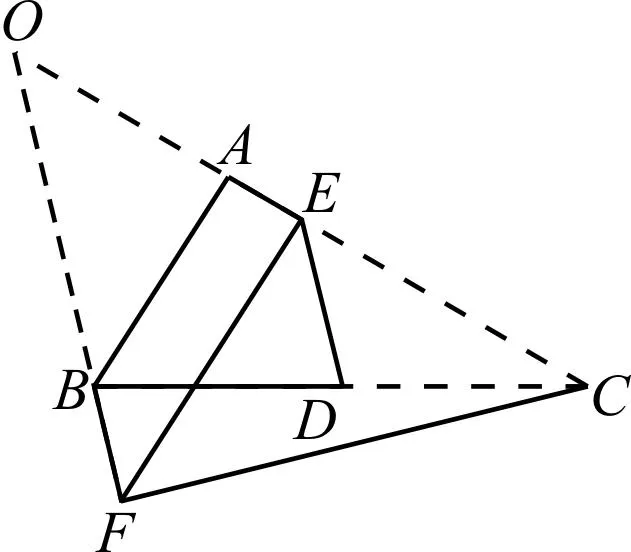
图5

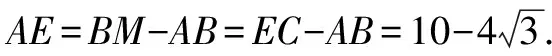
图6

点评：解法4和解法5均是通过延长边线形成交点,找到隐藏的特殊形状而求解.解法4中延长边线重点在于形成直角三角形,解法5则是通过延长边线,形成平行四边形.二者的相同之处均是在图形中找等腰三角形.笔者认为较思路一,这种通过延长线段添加辅助线的技巧比较难想到,但是证明较简单.正如在初三复习折叠的核心考点时,会出现“折叠遇平行,等腰必出现”的口诀,由此发掘出一些奇思妙构的解法.

思路三：取中点,构造三角形中位线.

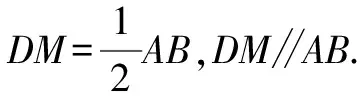
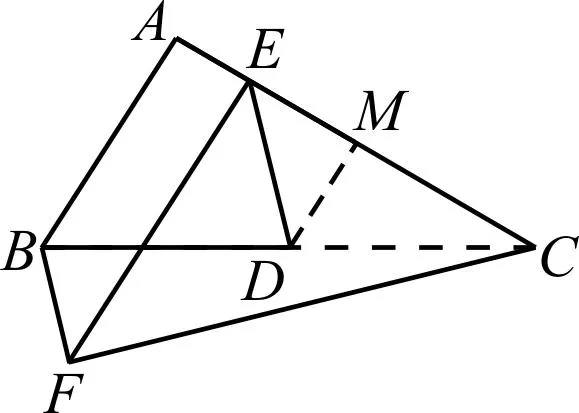
图7

点评：易知D为线段BC的中点,此解法聚焦几何问题的三大法宝之一——中点,通过构造中位线,快速转化已知条件.再结合另一法宝——平行,导边导角,找出线段间的等量关系,求解未知线段.

思路四：构造“八字全等”找等腰.

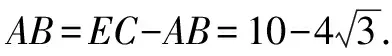
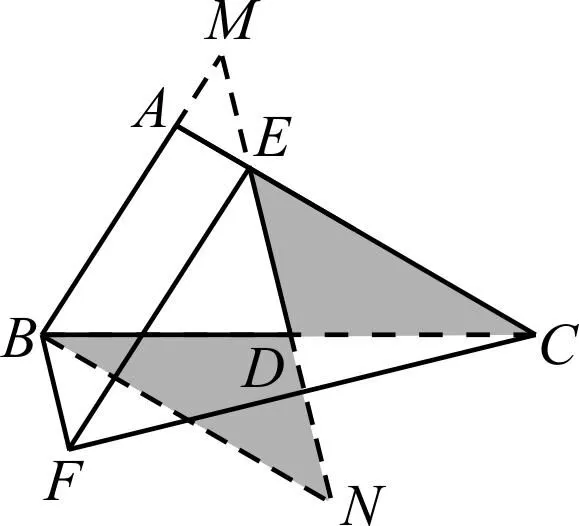
图8

点评：“八字模型”的建立依赖两个条件,即D为线段BC和线段EN的中点,但辅助线多而且难想,比较累赘.

4 变式训练

如图1,在△ABC中,D,E分别为线段BC,AC上一点,将△CDE沿DE折叠,使得C落在F处,则①∠BFC=90°,②EF∥AB,③AB+AE=EC这三个条件,任选两个都可推出另一个.感兴趣的读者可以试着证明.

注意:条件①也可换为“D是线段BC的中点”.

现在回过头看原中考题,其实线段长度可随便定,只要满足条件③即可.这就是该问题的变式思考.

教育家怀特海认为,教育需要使学生通过树木看见森林.回到题目本身,我们可以基于学情,科学、合理、有序地培养学生“解题非一法,寻思求百通”的意识.

5 通性通法

折叠问题,题型多变,因图形看起来比较复杂,不少学生望而生畏.其实几何图形的折叠问题,本质上就是轴对称问题.解决这类问题的关键是抓住折叠前后的两个图形全等,注意折叠前后变化的量和不变的量,然后抓住背景图的相关性质,利用转化或运用方程思想解决问题.在中考复习教学中,要以经典问题为主,预设不同解法和思路,但是要渗透万变不离其宗的解题思想,注重通性通法的总结.

6 题后反思

俗语说:心在一艺,其艺必工;一心在一职,其职必举.一题多解的数学之美不仅在于多,而且在于题后的对比和归纳.波利亚指出:“没有任何一道题可以解决得十全十美,总剩下些工作要做.”这里剩下的工作就是解题反思,它有助于学习者领悟思想方法和数学活动经验,实现从知识的学习到能力的提升.