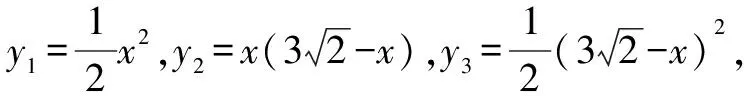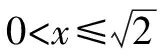运用转化思想解决初中函数应用题
⦿ 江苏省苏州市高新区实验初级中学 陈 惠
近几年各地的中考数学试题中,出现了一些设计新颖、贴近生活、反映时代特点的函数应用题.实际问题来源于生活,这些问题的解答要依赖于众多的数学思想和答题技巧.如函数思想、方程思想、数形结合思想和转化思想,其中转化思想贯穿解题的始终[1].具体来说,就是把具体实际问题转化为数学中的函数问题,把众多的变量(未知量)转化成用一个变量(或已知量)来表示,把复杂问题转化成一个或多个简单问题.
1 题型一:利用一次函数求最值类实际应用题
获取最大利润问题就是求函数的最值类问题,解决这类题的实质就是建立数学模型和求解数学模型的思维活动过程.主要运用转化思想,将实际问题和数学问题相互转化,使问题得以解决,解题思路如图1:
例1(2022年江苏省苏州市中考试题第25题)某水果店经销甲、乙两种水果,两次购进水果的情况如表1所示:
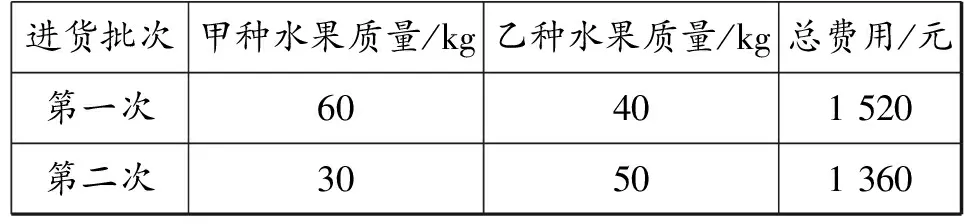
表1
(1)求甲、乙两种水果的进价;
(2)销售完前两次购进的水果后,水果店决定第三次购进甲、乙两种水果共200 kg,且投入的资金不超过3 360元.将其中的mkg甲种水果和3mkg乙种水果按进价销售,剩余的甲种水果以17元/kg、乙种水果以30元/kg的价格销售.若第三次购进的200 kg水果全部售出后,获得的最大利润不低于800元,求正整数m的最大值.
解析:(1)设甲种水果的进价为a元/kg,乙种水果的进价为b元/kg.

(2)设水果店第三次购进甲种水果xkg,则购进乙种水果(200-x)kg.
根据题意,得12x+20(200-x)≤3 360,解得x≥80.
设所得利润为w元,则w=(17-12)×(x-m)+(30-20)×(200-x-3m)=-5x-35m+2 000.
当x=80时,w取得最大值-35m+1 600.
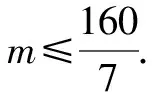
所以正整数m的最大值为22.
评析:本题主要考查一次函数的实际应用,解答本题的关键是在理解题意的基础上,找出等量关系,列出相应的二元一次方程,写出相应的函数解析式,再利用一次函数的性质求最值.
2 题型二:二次函数与几何相结合的实际应用题
这类问题综合性较强,既考查学生对各种几何图形、二次函数性质等的掌握情况,又侧重考查学生的实际动手操作能力.解决这类问题主要是运用转化思想,因此熟练掌握各种转换技巧显得十分重要.
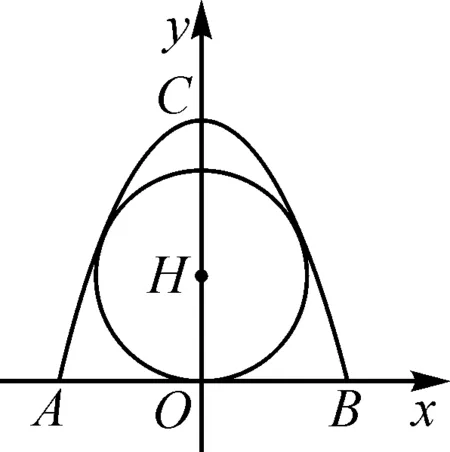
例2(2022年江苏省扬州市中考试题第27题)如图2是一块铁皮余料,将其放置在平面直角坐标系中,底部边缘AB在x轴上,且AB=8 dm,外轮廓线是抛物线的一部分,对称轴为y轴,高度OC=8 dm.现计划将此余料进行切割.

图2
(1)若切割成正方形,要求一边在底部边缘AB上且面积最大,求此正方形的面积;
(2)若切割成矩形,要求一边在底部边缘AB上且周长最大,求此矩形的周长;
(3)若切割成圆,判断能否切得半径为3 dm的圆,请说明理由.



图3
(2)如图4所示,矩形DEFG为符合题意的矩形.设DE=2n,则E(n,0)(0 图4 故当n=2时,矩形的周长最大,最大值为20 dm. 图5 所以,能切得半径为3 dm的圆. 评析:本题考查了二次函数与正方形、矩形、圆等几何图形相结合的综合性问题,突出实践操作能力.熟练掌握各图形的性质,能灵活运用坐标与线段长度之间的转换是解题的关键. 探索性问题是指根据已知条件(或给出的结论),探求相应结论(或条件)是否存在的一类问题.这类问题的解题思路是:假设存在—分类演绎推理—得出结论(合理或矛盾). 图6 (1)设CF=x,用含有x的代数式把Rt△AEP,Rt△PFB及矩形ECFP的面积表示出来; (2)是否存在这样的点P,使Rt△AEP,Rt△PFB及矩形ECFP的面积都小于4? 评析:本题考查了由给出结论探究点P的存在性问题.题中渗透了函数、数形结合、从特殊到一般、类比等数学思想方法.由于图形(点、线)的位置不同,会使结论产生多种情况,这时就要分类讨论,从面积相等的特殊情形到面积不等的一般情形. 运用转化思想解决与函数有关的实际问题,具有“化陌生为熟悉、化复杂为简单、化抽象为具体”的巨大优越性[2],能够帮助我们理清解题思路,快速找到解题的突破口,从而降低题目的难度系数,引领我们走出解题困境.
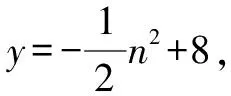
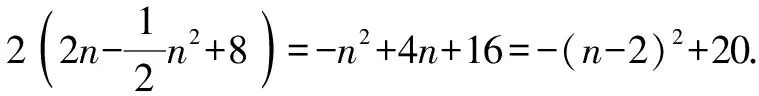
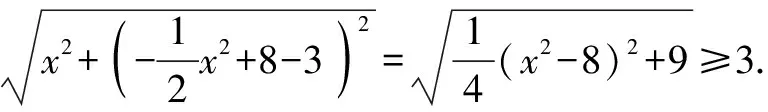
3 题型三:二次函数的探索性问题