问题驱动 深度参与 落实素养——以“二次函数应用”教学片段为例

⦿ 江苏省仪征市实验中学 余叶军 夏玉荣

近日,笔者在参加全市乡村共同体数学教研活动中,听了一节乡镇学校的初三数学课,课题是“二次函数的应用”.课后,笔者进行了师生访谈交流,并对学生进行了检测分析,交流结果与分析数据引发了笔者对本节课一个教学片段的思考.

1 教学实录片段

教者出示题目:某公司销售一批产品,该产品每件成本是40元,试销阶段每件产品的销售价x(单位:元)与产品的日销售量y(单位:件)之间满足一次函数关系,部分对应数据如表1.

表1

(1)求日销售量y与单件售价x的函数关系式.

(2)每件产品的销售价定为多少元,当天的销售利润最大?最大利润是多少?

(3)若售价为50元/件时,每天能卖出500件.商场想采用提高售价的方法来增加利润.已知这种商品每件涨价1元,销量就减少10件,为当天获取的利润不少于8 000元,应怎样定价?

师:这是一道常见的二次函数的应用问题,现在请一个同学来展示一下第(1)问.

生1:设一次函数的解析式为y=kx+b,利用待定系数法将点(45,25)和(50,20)代入,解得k=-1,b=70,所以一次函数解析式为y=-x+70.

师:很好,再请一个同学来展示一下第(2)问.

生2:因为每件产品的利润为(x-40)元,日销售量为(-x+70)件,设总利润为z元,所以可得z=(x-40)(-x+70),再利用配方法可以求出结果.

师:很好,同学们非常快速地解决了前面两个小问.下面请大家思考一下第(3)问,先独立思考,再互相交流一下(学生思考几分钟时间).

生3:设每件涨价x元,则售价为(50+x)元/件.设总利润为z元,则z=(50+x-40)(500-10x).因为当天获取的利润不少于8 000元,所以可以得到(50+x-40)(500-10x)≥8 000.不等式我不会解了.

师:将z=(50+x-40)(500-10x)配方,可得y=-10(x-20)2+9 000.又z≥8 000,这个不等式的解法估计大部分同学想不到.究竟怎么解决呢?请大家看投影展示.

由图1可知,当10≤x≤30时,8 000≤y≤9 000,所以单件产品定价为60元至80元时,日利润不少于8 000元.

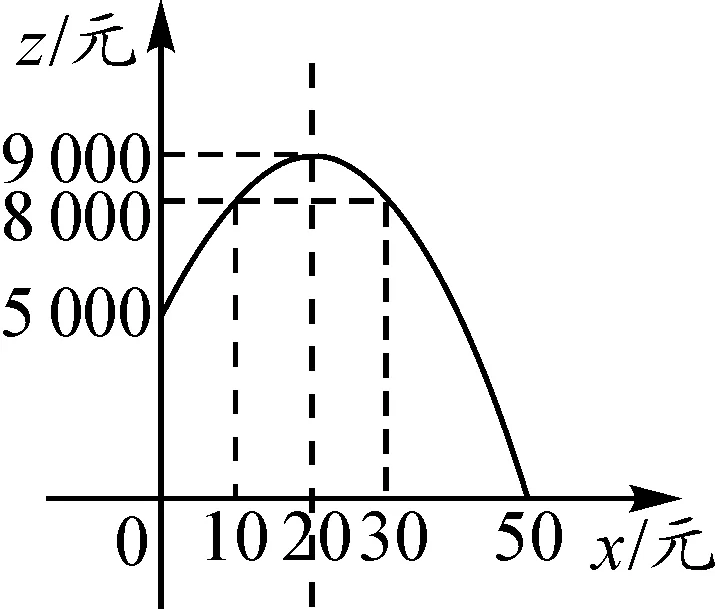
图1

然后,教者开始讲授其他新课内容了．

2 课后师生交流,检测反馈分析

这道例题的教学,看似让学生理解了解法,也充分展示和暴露了学生的思维过程,但这样的讲法只是徒有其表,尤其是第(3)问的讲解只是教师展示了答案,并强调了注意点,真正留给学生的解题经验与数学思想寥寥无几.教者依然没有摆脱题海思维,这样的例题教学收效甚微.笔者以为这道数形结合题的教学不太成功,教师没有深入研究问题,没有将问题的本质充分展示给学生.这道习题教学的意义是什么?学生的典型错误在哪里?借助这次讲评,学生有没有理解数形结合的意义?为此,笔者课后与师生进行了充分交流,并重新设计了两道测试题用来检测数形结合教学的质效.

2.1 课后与教师的互动交流

笔者:您选择这道题目的目的是什么?

教者:因为这种题型在中考中经常出现,属于二次函数应用的热点,很典型,而且学生做这类题也有难度,整体的达成度不高.

笔者:您讲评这道习题的侧重点在哪?

教者:因为这道题前两问学生能解决．但第(3)问很多学生做不出来,我主要讲第(3)问,用数形结合方法解决实际问题.

笔者:您认为前两问学生的达成度有多少?

教者:前两问比较简单,我没有具体统计,学生的准确性应该还可以吧.

笔者:您认为第(3)问的讲解学生听懂了多少?

教者:我已经让学生回答,学生没答出,因为数形结合对于学生来说是一个难点,学生都是用不等式来解决,而初中阶段一元二次不等式学生没办法解决,所以给学生展示了比较完整的解答过程,同时也进行了强调,应该收到了良好的效果.

2.2 课后与部分学生的交流

笔者:这种题型平时遇到的多吗?

学生(众人):经常遇到.

笔者:对于这道题,你们都能听懂吗?假如现在再面临同样的问题,能熟练求解吗?

学生1:前面两问听懂了,但是第(3)问的解法不是太明确,以后我再遇到估计做对的把握不大．

笔者:第(2)问的结果老师没有呈现,你们算出来了吗?

学生(众人):我也不知道对不对,老师说配方,我用的是公式法.

笔者:第(3)问老师不是已经完整地展示了解题过程吗?怎么还会有疑问呢?

学生3:我首先想到的是运用不等式的知识来解决问题,至于后面老师为什么要画图象,怎么会想到画图象,图象画出来怎么用,我还是比较费解的.

笔者:你觉得老师设置的这几个问题,关联性与层次性是否明显?

学生4:我觉得这三个问题有一定的关联性,但层次不明显,之间的跨度有点大,结构不是太合理.

2.3 测试情况及统计分析

是否如老师所言,对于类似的问题学生能够熟练求解?如果给出类似的习题,学生还能解决吗?为此,笔者设计了两个问题用以检验学生的学习效果,问题如下:

(1)如图2,已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4)和B(8,2),则能使y1>y2成立的x的取值范围为______.

图2

(2)(2016·扬州)某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0)．未来30天,这款时装将开展“每天降价1元”的促销活动,即从第1天起每天的单价均比前一天降1元．通过市场调研发现,该时装单价每降1元,每天销量增加4件．在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为______.

两道检测题的统计分析见表2.

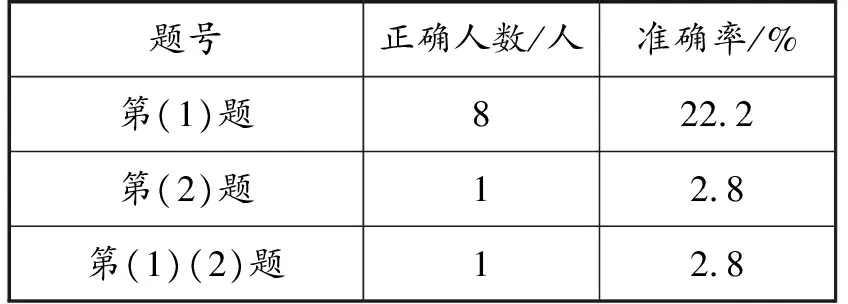
表2

虽然是乡村薄弱学校,但是通过统计分析发现,学生检测的结果也太差了,班级36人参加测试,两题全对的只有1人．由此说明,通过这个例题的教学,学生并没有真正领悟到如何看图象,遇到实际问题还不能够借助函数图象灵活解决问题．

3 教学思考

(1)关注学生的体验,让学生在问题中感悟学习

学生已有的认知经验是进行数学学习活动的基础,当我们遵循这样的本质规律,那么新知识的生长点也就具备了,学生就会在已有经验的基础上,通过教师有效的问题对后续的学习有所感悟.在课堂教学中,教师应抓住这一本质,搭建新旧知识之间的桥梁,借助开启学生思维的问题,帮助学生复习已有知识,铺垫好新学知识.

(2)关注学生的能力,让学生在问题中探究学习

问题是开启学生思维的钥匙,在关注学生能力的同时,教师要设置有层次性、递进性的问题,由浅入深,由表及里,层层深入,引导学生抽丝剥茧,使得他们的思维在探究中步步深入,体验学习的乐趣.

(3)关注课堂的辐射,让学生在问题中创新学习

一节课给学生留下的不仅是知识,更重要的是思想方法.数学课堂上,教师要通过数学抽象、数学建模,提升学生用数学的眼光观察现实世界的素养.在实际操作中训练学生的数学抽象能力,让数学即生活的价值在脑海中自然流淌.

《义务教育数学课程标准(2022年版)》指出:会用坐标表达图形的变化、简单图形的性质,感悟通过几何建立直观、通过代数得到数学表达的过程.在这样的过程中,感悟数形结合思想,会用数形结合的方法分析和解决问题.可见,感悟数形结合思想,会用数形结合的方法分析和解决问题是新课程标准对数学教学的基本要求.为此,教师要通过具体现实的数学情境,引导学生学会从几何的角度发现问题和提出问题,进而学会用几何直观和逻辑推理思想去解决问题,切实实现利用问题驱动,引导学生深度参与课堂,进而提升核心素养的培养.