加强多元表征策略研究,提升几何直观核心素养

⦿ 江苏省南通市海安市墩头镇墩头初级中学 周存兰

在初中阶段数学知识的学习过程中,充分利用多元表征理论进行学生几何直观能力培养,可以多方面引导学生对数学问题的理解与研究,也更容易帮助学生理解把握一些数学问题的本质.采用多种表征转换,更有助于学生深入学习,可以达成更好的学习效果.本文中就多元表征的应用策略进行研究,以更好地提升学生的几何直观核心素养.

1 丰富语言情境,提升几何直观的“纯度”

在解答一些数学问题的过程中,往往会遇到很多以文字为主的问题,特别是涉及到数学古代文化知识问题,需要对这些问题进行语言转化,有时还需要将相关的问题情境利用图形语言或者符号语言表达出来,这样才能更容易把握问题的本质.利用几何图形展示问题特征,会使得问题更加直观形象,能激发学生的学习兴趣,更能引导学生对问题的探究分析,充分彰显文化特色.

例1我国古代著名的数学家刘徽著有《海岛算经》．内有一篇:“今有望海岛,立两表齐,高三丈,前后相去千步,令后表与前表相直．从前表却行百二十三步,人目著地取望岛峰,与表末参合．从后表却行百二十七步,人目著地取望岛峰,亦与表末参合．问岛高及去表各几何?”请你计算出海岛高度为______步．(提示:三丈二5步.)

分析：此类问题,不光在语言上给学生们设置了障碍,在分析解决问题的过程中还有更多的难点.针对此类问题,单纯从字面上来理解,学生很难入手计算,这就需要教师帮助学生转化语言描述,用更简单、更直接的文字将题意表述出来,再借助相关的数据提示,如两根标杆高均为5步、前后相距1 000步、退行123步等.这样的转化,学生起码在阅读上没有了障碍,而如何解答计算此问题,又成了学生突破的难点.因此,再根据题意,将文字语言转化为图形语言,使复杂的问题简单化,最终转化为相似三角形对应边成比例的问题,从而可根据数量之间的关系列出分式方程,即可求出岛高．

2 加强动态展示,提升几何直观的“维度”

在一些有难度的数学问题中,有时很难发现它的切入点,特别是涉及最值的问题,在什么情形下才能达到最小或最大呢?有些问题光靠观察分析很难解决,如果将静态问题转化为动态问题来分析,将问题从“一维”转化为“多维”来思考,将平面问题转化为立体问题来观察,这样问题会更加生动直观,能更加吸引学生的注意力,便于解决问题[1].

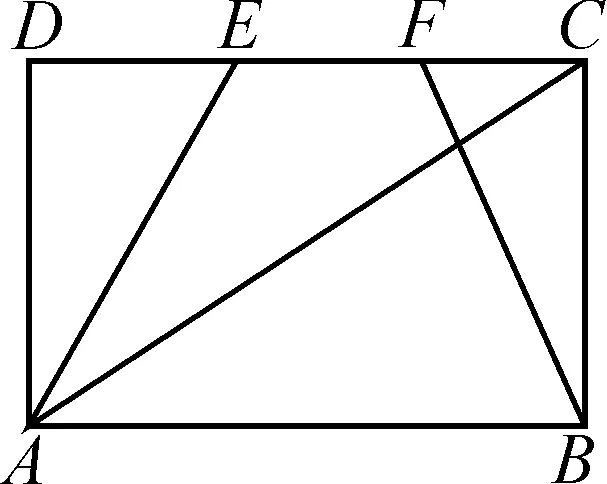
图1

图2

3 强化数形结合,拓展几何直观的“深度”

“数”与“形”相辅相成,二者在某种程度上可以互相转化,借助图形来表示数之间的某种关系,借助数的精确性来阐明图形特点.只有在解决问题的过程中不断深入强化数形结合的表征,才能更好地引导学生进行数形思维转化,从而更好地把握数形规律,拓宽学生几何图形的直观辨别度.

(2)如图3,正方形网格中小正方形的边长为1,在格点上有两个点,分别为A,B,且满足AB=7．请在线段AB上找一个点P,使AP的长为(1)中所求的x,并在图形中画出点P位置,写出结论即可．

图3

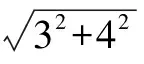
对于第(2)小题,通过作图,得到图4,这样可证明△APC′∽△BPD,列比例式即可求出x的值．

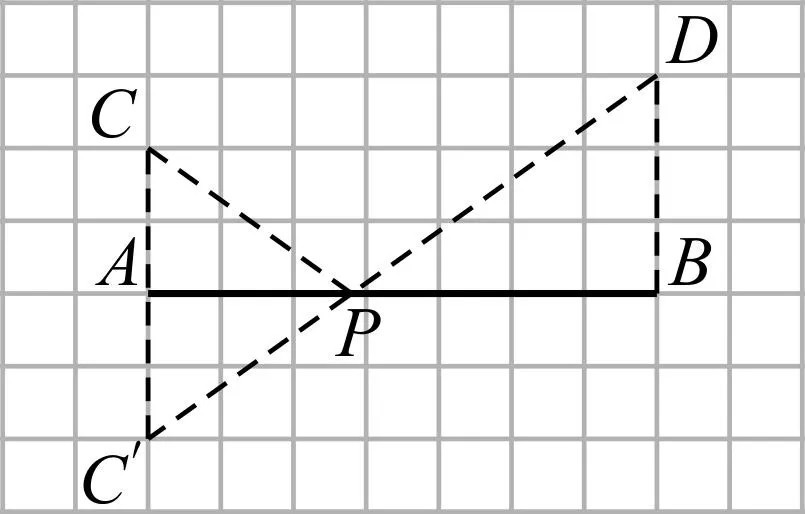
图4

我国著名的数学家华罗庚曾说过:“形缺数时难入微,数缺形时少直观.”这句话很明显点出了数形结合的特点,“数”与“形”缺少哪一方面都不是完美的数学,并且告诉我们,解决数学问题要注意利用“数形结合”法,注意“数”和“形”的互相转化.根据实际问题所描述的情境,将数与形有机联系在一起,可将复杂问题简单化,将抽象问题直观化.

4 开展实践操作,拓展几何直观的“宽度”

数学学习活动离不开实际操作.在数学教学中重视动手实践操作活动的开展,能更有利于发展学生的创新思维,增强数学问题的直观性,能更好地拓展学生几何直观的宽度,让学生在操作中探究问题的本质,从而更容易接收相关知识,解答也会变得更加容易[2].

例4现有如图5所示的若干个边长为a的小正方形纸片①,长为b、宽为a的长方形纸片②,以及边长为b的大纸片③．请解决下列相关问题.

图5

(1)如果小正方形①的纸片有1张,大正方形③的纸片有1张,长方形②的纸片有3张,利用这些纸片你能否将它们拼成一个大长方形(如图6所示)?结合各个纸片表示的面积之间的大小关系将多项式a2+3ab+2b2分解因式.

图6

(2)如果现有上面所描述的三种纸片各8张,从其中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(按原纸张进行无空隙、无重叠拼接),那么可以拼成多少种边长不同的正方形?

分析：实际上,这样的问题对于学生来说既抽象又难以理解,本来整式问题对他们来说就感觉摸不着头脑,解决此类应用问题更是难上加难.如果将问题转化为实际操作问题,让学生准备类似的硬纸片,剪成相对应的形状,再操作摆放,并在摆放过程中引导学生不断总结摆放的一些方法或技巧,让学生在操作中分析,在操作中思考、总结,借助剪切的动态设计,引导学生对问题进行研究.这样不仅加强了学生的空间想象力,更提高了他们的几何直观能力,在摆放过程中找到了边与边的关系,找到了多项式与图形之间的关系,找到了面积与图形之间的关系,从而顺利突破难题.

综上所述,可以发现只有充分调动数学的多元表征,关注公式、概念、性质的“数”的特点以及数学模型、几何图形的“形”,将“数”与“形”完美结合,充分体现几何直观的优势,才能让学生在提高直观能力的基础上,进一步提升数学核心素养,真正体现几何直观的价值.