活用辅助线,巧妙建立联系——以初中几何解题教学为例

⦿ 哈尔滨师范大学教师教育学院 李轶男

在初中数学教学体系中,利用几何知识解题历来是一块“难啃的骨头”.在这一背景下,学生唯有掌握辅助线的应用技巧,合理构造辅助线,才能构建出全新的条件,扫清解题中的障碍.构建必要的辅助线,不仅能够揭示图形的本质,帮助学生更好地探索图形背后的性质,还可以借助辅助线增强学生的问题分析能力,发展学生的空间观念等数学核心素养.基于此,结合新课程标准的要求,鉴于学生解题的需求,培养学生构建辅助线的能力已经成为一项重要的教学任务.

1 辅助线在初中几何解题中的具体应用

针对初中生来说,所学的几何内容主要涉及三角形、四边形、圆等基本内容.按照新课程标准的要求,教师在日常教学中应培养学生的几何直观意识、几何推理能力等.因此,在几何教学中,引导学生运用辅助线解决问题,已经成为一种必然.

1.1 构建分割型辅助线

在解答初中几何问题时,构建分割型辅助线比较常见.顾名思义,分割型辅助线就是将图形中已有的两个点连接起来,借助所作的辅助线,将原来的图形进行分隔,使其成为新的几何图形,并由此产生新的条件,以便于问题求解.

例1如图1所示,在△ABC中,∠B=90°,AB=BC,BD=CE,M是AC边上的中点,求证:DM=ME.

图1

分析：将线段DM与ME置于两个不同的三角形中,借助三角形全等进行证明.

证明：如图2,连接BM.

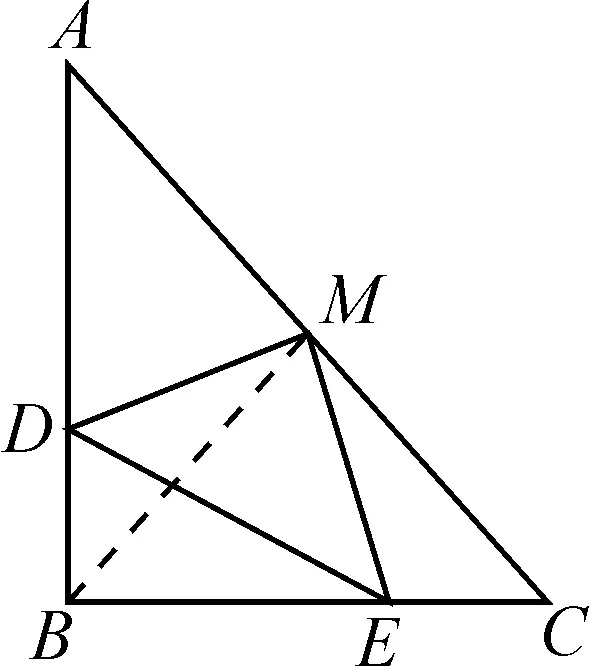
图2

∵AB=BC,

∴∠A=∠C.

又M是AC边上的中点,

∴AM=BM=MC.

∴∠MBE=∠C=∠A.

∵BD=CE,

∴AD=BE.

∴△MDA≌△MEB(SAS).

∴DM=ME.

1.2 构建延长型辅助线

延长型辅助线也是初中几何中最为常见的辅助线类型之一,即将原来图形中的某一条线段延长,最终形成一个新的图形,以便于问题解答.通常,这种辅助线应用在特征不甚明显的几何题目中,无论是连接两点,或者作垂线,学生都很难完成解答.此时,就可选择延长型辅助线,构建出新的图形,引出新的数量关系.

例2如图3所示,已知AD+BC=2,AB=CD=2,∠A=60°,求四边形ABCD的面积.

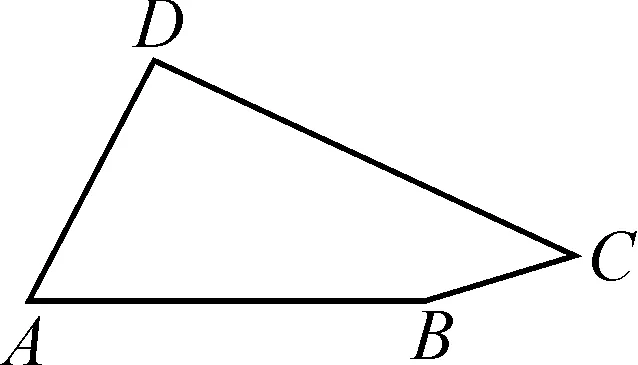
图3

分析：本题无论是连接BD,还是连接AC都难以解答.面对这一现状,可选择构建延长型辅助线的方式进行解答.

解：如图4,延长AD至点E,使得AE=AB,连接BE,BD.

图4

∵∠A=60°,AE=AB,

∴△ABE为等边三角形.

∴BE=AB=CD=2.

又AD+BC=2,AD+DE=2,

∴BC=DE.

∴△DBC≌△BDE(SSS).

1.3 构建平移型辅助线

平移型辅助线在初中几何解题中也尤为常见.具体来说,平移型辅助线就是在原有的图形中,针对某条线段展开平移,使其成为辅助线,最终形成新的图形,并构造出新的条件关系等,以便于更好地解题.

例3如图5,已知直角梯形ABCD,CD∥AB,∠A=90°,AB=12,BC=10,AD=8,求CD的长度.

图5

分析：单纯地结合图形,以及题目中所给出的条件和数量关系,很难求出CD的值.鉴于本题的特征,可采用平移型辅助线的方式求解.

解：如图6,过点D作DE∥BC交AB于点E.

图6

又CD∥AB,

∴四边形CDEB为平行四边形.

∴CD=BE,BC=ED=10.

在Rt△ADE中,由勾股定理得AE=6.

∴CD=BE=AB-AE=6.

1.4 构建对称点型辅助线

在初中几何题目中,对称点常常是解题的关键.当题目中已有的条件无法满足解题需求时,即可发挥对称点的价值,以此切入点构建辅助线,进而构建出新的条件和数量关系,最终完成题目的解答.

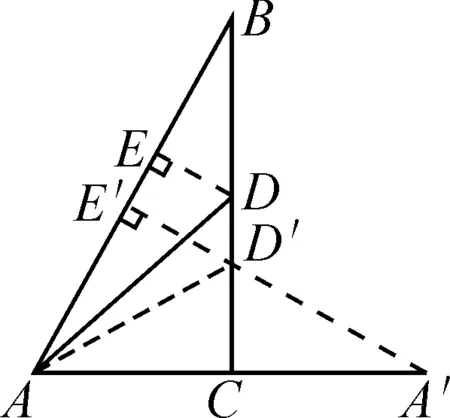
图7

∵∠C=90°,AC=1,

∵∠D′AC=∠A′=∠B=30°,

1.5 构建中点型辅助线

在几何题目中,中点型辅助线也很常见,尤其是当题目中出现了“中线”“中点”等条件时,就可通过三角形、梯形的中位线定理,构建相关的辅助线,最终实现题目的解答.

例5如图8所示,已知E,F分别是线段BC,AD的中点,且AB=CD,直线BA,EF相交于点G,直线CD,EF相交于点H,证明:∠BGE=∠CHE.

图8

分析：由于题目中给出了中点E,F,由此可采用中点型辅助线在原来的图形中构造出一个新的三角形.

证明：如图9,连接AC,并取AC上中点P,连接PE,PF.

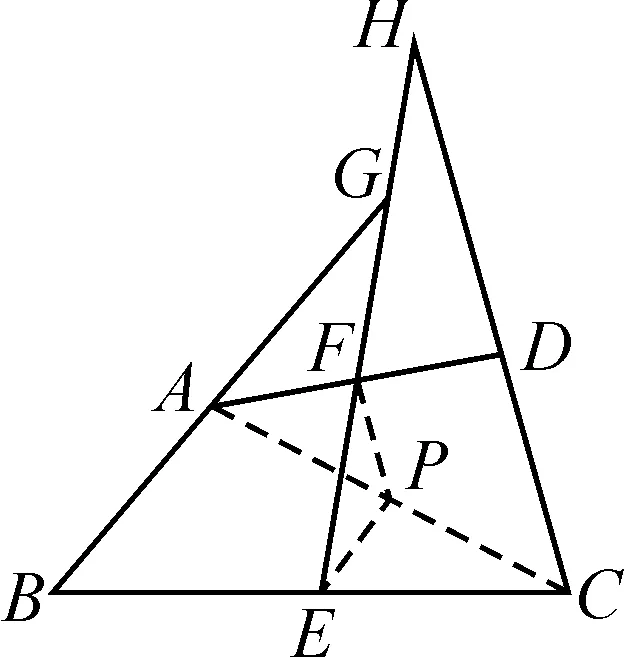
图9

∵E为BC的中点,

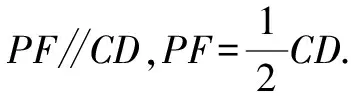
又AB=CD,

∴PE=PF.

∴∠PEF=∠PFE.

∵PE∥AB,

∴∠BGE=∠PEF.

同理,得∠CHE=∠PFE.

∴∠BGE=∠CHE.

综上所述,辅助线是初中几何解题的“重要利器”,尤其是当思路不明、条件不够时,只要作出一条简单的辅助线,就能顺利找到解决问题的“突破口”.同时,掌握辅助线在解题中的应用,也是学生在潜移默化中逐渐形成的.因此,教师在日常教学中,应结合不同类型的题目,引导学生对辅助线进行归类总结,帮助学生掌握不同类型辅助线的应用条件,以便于在日后做题中,能够结合不同类型的题目,迅速、正确作出辅助线,最终完成题目的解答.