巧用隐圆解答初中数学最值问题

⦿ 江苏省南通市通州区实验中学 张 剑

隐圆是指题目中并未直接给出圆的图形,需根据对题设条件的判断画出的圆[1].运用隐圆解答初中数学最值问题的关键在于熟悉隐圆的常见情境,正确迅速找到并画出隐圆,注重圆性质的活用以及最值问题的转化.

1 隐圆应用情境分析

初中数学最值问题情境多样,涉及的隐圆情境主要有动点定长、直角圆周角、定弦定角、四点共圆四种[2].构建四种隐圆情境模型,可给初中数学最值问题的高效解决带来明确指引.动点定长情境源于圆的概念,情境中的动点到已知点(圆心)的距离(半径)保持不变.直角圆周角情境中固定线段所对的动角为直角(90°),直角顶点的轨迹是一个圆.定弦定角情境中线段长度不变,线段外一点与线段两端点连线构成的夹角不变,该点的轨迹是一个圆[3].四点共圆分为两类:对角互补的四边形四个顶点共圆;固定线段所对同侧两个动角相等,线段两端点和两个动角顶点共圆,如图1所示,∠C=∠P,则A,B,C,P四点共圆.

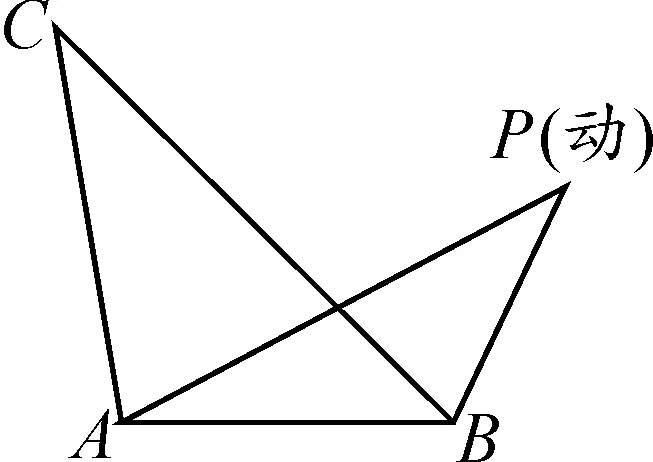
图1

2 隐圆在解题中的应用案例

例1如图2,等腰三角形ABC中,AB=AC=5,BC=6,D为BC的中点,E是AB上一动点.点B关于DE的对称点B′在△ABC内(不在△ABC的边上),则BE的最小值为______.

图2

解：由题中条件可得BD=DC,AD⊥BC.

图3

由图3可知,当BE最小时,B′在AB上,DE⊥AB.

思路解读：由点关于直线对称以及中点知识判断此题属于隐圆中动点定长情境.根据题意画出隐圆,找到点B′的特殊位置,多次使用勾股定理求得结果.

例2如图4所示,四边形ABCD中,AB∥CD,∠ACB=90°,∠DAB=60°,AD=CD=4,在其内部有一动点M,满足AM⊥DM,则△MBC面积的最小值为______.

图4

解：由四边形ABCD中,AB∥CD,∠DAB=60°,可得∠ADC=120°.

由AD=CD=4,可得∠DCA=∠CAB=30°.

在△ACB中,由∠ACB=90°,得∠B=90°-∠CAB=60°,所以梯形ABCD为等腰梯形.

如图5,取AD的中点O,连接OM.过点M,O分别向BC的延长线作垂线,垂足分别为点E,F,OF与DC交于点G,则ME∥OF.

图5

由∠B=60°,得∠FCG=60°,∠DGO=∠FGC=90°-∠FCG=30°,于是△DOG为等腰三角形,则AD=BC=4,DO=DG=2,所以

所以,△MBC面积的最小值为

思路解读：由题目中AM⊥DM这一关系,取AD的中点O,易知此题为隐圆中的直角圆周角情境.结合梯形的性质,求出BC的长.作出辅助线,借助平行线以及ME,OF,OM的关系求出BC边上的高,问题便迎刃而解.

图6

解：如图7,连接EC,由AP∥BC,可得∠ACB=∠PAC=∠PEC=60°,则∠BEC=120°.

图7

由∠ACB=60°,得∠ACM=90°.

连接AM与圆M交于点E′,则AE的最小值为AE′,ME′=MC=8.

在Rt△ACM中,由勾股定理,可得

所以AE′=AM-ME′=10-8=2.

故AE的最小值为2.

思路解读：由已知条件中的角度关系间接求出∠BEC=120°,根据定弦定角确定点E的轨迹为圆.运用圆的性质确定点E的位置,进一步推理得出△AMC为直角三角形,进而运用勾股定理求得最终结果.

例4如图8,Rt△ABC中,∠ACB=90°,BC=3,AC=4,∠A=∠CPB,过点C作CQ⊥PC交PB的延长线于点Q,则CQ的最大值为_____.

图8

解：由PC⊥CQ,得∠PCQ=90°.

CQ的值最大意味着PC的值最大.

易知A,C,B,P四点共圆,PC的最大值为圆的直径.

思路解读：由已知条件中∠A=∠CPB推理出A,B,C,P四点共圆且点P是运动的.根据图形中的角边关系通过△ABC∽△PQC,构建CQ和PC的关系,结合直径是圆中最长的弦,求出CQ的最大值.

3 结语

利用隐圆解答初中数学最值问题,无外乎上文中介绍的四种情境.吃透这四种情境,掌握四种情境中点、线、角等的特点,分析四种情境适宜解决的不同问题类型,配合经典例题的训练以及解题思路的梳理,牢固掌握应用思路与细节,可促进学生解题能力的有效提升.