聚焦构造函数解决导数问题的常见题型
■广东省汕头市澄海凤翔中学 徐春生
高考中有这样一类题型,题目中不给出具体的函数解析式,而是给出函数f(x)及其导数满足的条件,需要同学们据此条件构造抽象函数,再根据条件得出构造函数的单调性,应用单调性解决问题,该类试题具有一定的难度。
一、只含f'(x)
例1已知函数y=f(x)(x∈R)满足f(2)=1,且f(x)的导函数f'(x)<1,则f(x)>x-1的解集为( )。
A.(-2,2)
B.(-∞,-2)∪(2,+∞)
C.(-∞,2)
D.(2,+∞)
解析:设g(x)=f(x)-(x-1),则g'(x)=f'(x)-1<0,所以g(x)在R 上单调递减。因为f(2)=1,所以g(2)=f(2)-(2-1)=0。由f(x)>x-1,得g(x)>0,解得x<2。所以f(x)>x-1 的解集为(-∞,2),选C。
点评:若f'(x)>k(或<k)(k≠0),则构造函数F(x)=f(x)-kx或F(x)=f(x)-kx+b。
例2(多选题)设f(x),g(x)是定义域为R 且恒大于0的可导函数,若f'(x)·g(x)-f(x)g'(x)<0,则当a<x<b时有( )。A.f(x)g(x)>f(b)g(b)B.f(x)g(b)>f(b)g(x)C.f(x)g(a)<f(a)g(x)D.f(x)g(x)<f(a)g(a)
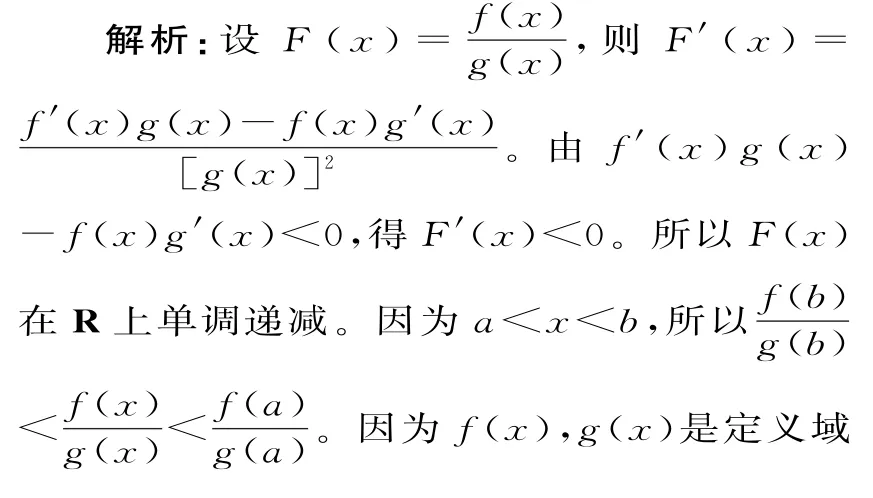
二、含f'(x)±f(x)
例3已知定义域为R的函数f(x)满足f(x)<-f'(x),则下列式子成立的是( )。
A.f(2 023)>ef(2 024)
B.f(2 023)<ef(2 024)
C.ef(2 023)>f(2 024)
D.ef(2 023)<f(2 024)
解析:依题意得f(x)+f'(x)<0,设g(x)=exf(x),则g'(x)=exf(x)+exf'(x)=ex[f(x)+f'(x)]<0在R上恒成立,所以函数g(x)=exf(x)在R上单调递减。
因为2 023<2 024,所 以g(2 023)>g(2 024),即e2023f(2 023)>e2024f(2 024),也 即f(2 023)>ef(2 024),故选A。
点评:若f'(x)+nf(x)>0(或<0),则构造函数F(x)=enxf(x),其中当n=1时,构造函数F(x)=exf(x)。
例4若函数y=f(x)的定义域为R,对于∀x∈R,f'(x)<f(x),且f(x+1)为偶函数,f(2)=1,则不等式f(x)<ex的解集为( )。
A.(2,+∞) B.(0,+∞)
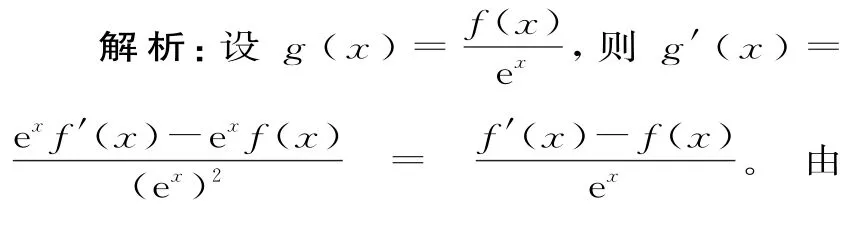
C.(-∞,0) D.(-∞,2)f'(x)<f(x),得f'(x)-f(x)<0,g'(x)<0,所以函数g(x)在R 上单调递减。由f(x+1)为偶函数,得函数f(x)的图像关于直线x=1对称。
因为f(2)=1,所以f(0)=1,g(0)=
不等式f(x)<ex整理得,即g(x)<g(0),所以x>0。
所以不等式f(x)<ex的解集为(0,+∞),选B。
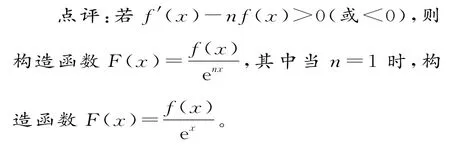
三、含xf'(x)±f(x)

点评:若xf'(x)+nf(x)>0(或<0),则构造函数F(x)=xnf(x),其中当n=1时,构造函数F(x)=xf(x)。
例6已知定义域为R 的奇函数f(x)的 导 函 数 为f'(x),当x>0 时,xf'(x)-f(x)<0,若,b=,则a,b,c的大小关系正确的是( )。
A.a<b<cB.b<c<a
C.a<c<bD.c<a<b

四、含f'(x)tan x±f(x)

五、含f'(x)±f(x)tan x
例8(多选题)已知定义在上的函数f(x)的导函数为f'(x),且f(0)=0,f'(x)cosx+f(x)sinx<0,则下列判断中正确的是( )。
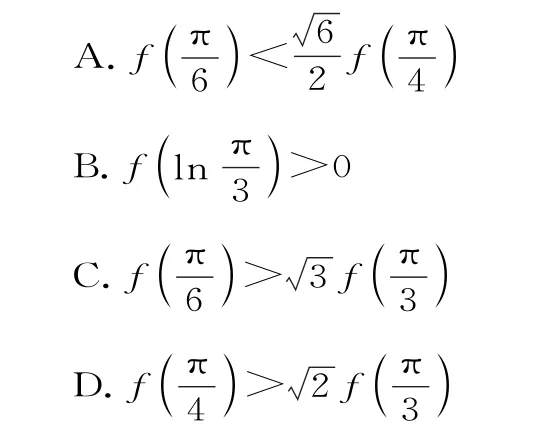
故选CD。
点评:若f'(x)-f(x)tanx>0(或<0),则构造函数F(x)=f(x)cosx;若f'(x)+f(x)tanx>0(或<0),则构造函数F(x)

