突出本质,体现综合,重视应用,彰显素养
■河南省洛阳市第一高级中学 王伟琪
普通高中数学课程标准将数列内容纳入函数主题中,其内容要求为:了解数列的概念;探索并掌握等差数列和等比数列的变化规律,建立通项公式和前n项和公式;能运用等差数列、等比数列解决简单的实际问题和数学问题;感受数列与函数的共性与差异,体会数学的整体性。
随着高考评价改革、高中育人方式改革的推进,高考试题的命制也发生了很大的变化。近几年的高考数学试题全面考查数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析的核心素养,体现基础性、综合性、应用性和创新性的考查要求,突出理性思维,发挥数学学科在人才选拔中的重要作用。近几年高考数学试题的数列部分,能够准确体现高考内容改革的要求,遵循高中数学课程标准,考查“四基四能”,突出本质,体现综合,重视应用,彰显素养。
一、考查数列基本量
此类问题主要考查数列的概念,数列的通项及数列基本量的计算。
例1【2023年新课标Ⅰ卷第7题】记Sn为数列{an}的前n项和,设甲:{an}为等差数列;乙为等差数列,则( )。
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
解析:(方法1)甲:{an}为等差数列,设其首项为a1,公差为d。
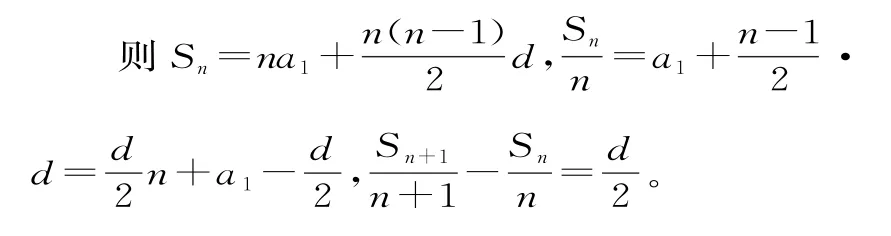
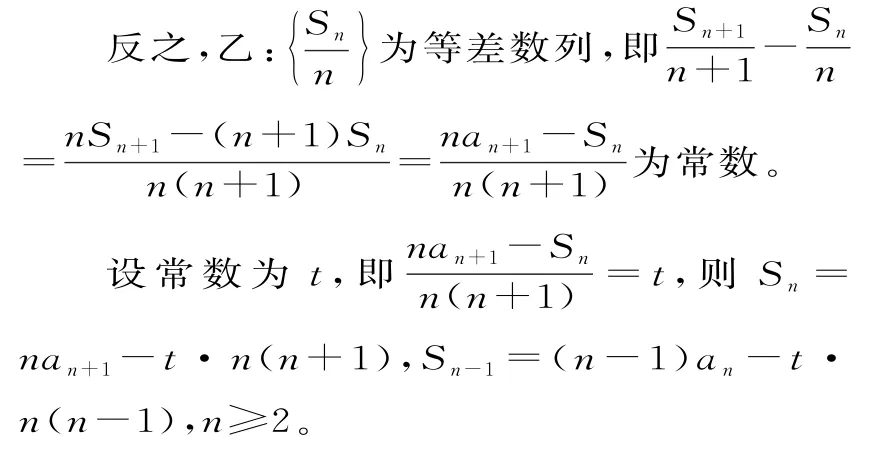
两式相减得an=nan+1-(n-1)an-2tn,即an+1-an=2t,对n=1也成立。
因此,{an}为等差数列,甲是乙的必要条件。
故甲是乙的充要条件,选C。
(方法2)甲:{an}为等差数列,设数列{an}的首项为a1,公差为d,即Sn=na1+
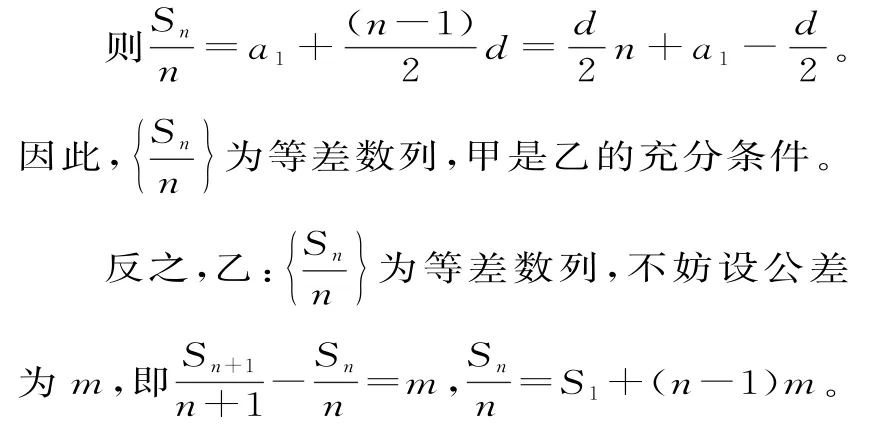
故Sn=nS1+n(n-1)m,Sn-1=(n-1)·S1+(n-1)·(n-2)m。
当n≥2时,以上两式相减得Sn-Sn-1=S1+2(n-1)m。
于是an=a1+2(n-1)m。
故an+1-an=a1+2nm-[a1+2(n-1)·m]=2m为常数,{an}为等差数列,甲是乙的必要条件。
故甲是乙的充要条件,选C。
二、考查等差数列和等比数列的性质
此类问题灵活考查等差数列和等比数列的基本性质。
例2设等差数列{an}的前n项和为Sn,已知Sm-1=-2,Sm=0,Sm+1=3,则m=( )。
A.3 B.4 C.5 D.6
解析:(方法1)由题意得:

三、考查{an}与Sn 的关系及数列求和
此类问题主要考查{an}与Sn的关系及数列求和的基本方法,如错位相减法、裂项法、拆项法等。
例3【2021 年全国乙卷理数第19题】记Sn为数列{an}的前n项和,bn为数列{Sn}的前n项积,已知
(1)证明:数列{bn}是等差数列;
(2)求{an}的通项公式。

(方法2)由已知条件得bn=S1·S2·S3·…·Sn-1·Sn。①
于是bn-1=S1·S2·S3·…·Sn-1(n≥2)。②

四、考查周期数列

例5【全国高中数学联赛试题】已知数列{xn}满足xn+1=xn-xn-1(n≥2),x1=a,x2=b,记Sn=x1+x2+…+xn,则下列结论正确的是( )。
A.x100=-a,S100=2b-a
B.x100=-b,S100=2b-a
C.x100=-b,S100=b-a
D.x100=-a,S100=b-a
解析:考查周期数列,易得周期T=6。x1=a,x2=b,x3=b-a,x4=-a,x5=-b,x6=a-b,选A。
五、考查数列的应用与数学文化
此类问题考查考生数学建模能力,审题意识和应用意识
例6【2020 年全国新课标Ⅱ卷第4题】如图1,北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层,上层中心有一块圆形石板(称为天心石),环绕天心石砌9 块扇面形石板构成第一环,向外每环依次增加9块,下一层的第一环比上一层的最后一环多9块,向外每环依次也增加9 块。已知每层环数相同,且下层比中层多729块,则三层共有( )扇面形石板(不含天心石)。

图1
A.3 699块 B.3 474块
C.3 402块 D.3 339块
解析:设第n环天心石块数为an,第一层共有n环,则{an}是以9为首项,9为公差的等差数列,an=9+(n-1)×9=9n。
设Sn为{an}的前n项和,则第一层,第二层,第三层扇面形石板的块数分别为Sn,S2n-Sn,S3n-S2n。
因为下层比中层多729 块,所以S3n-S2n=S2n-Sn+729。

六、考查数列的奇偶项求和问题
此类问题一般难度比较大,考查同学们的观察能力、运算能力、逻辑推理能力及转化与化归意识。
例7【2020 年全国Ⅰ卷文数第16题】数列{an}满足an+2+(-1)nan=3n-1,前16项和为540,则a1=_____。
解析:当n为偶数时,有an+2+an=3n-1。
故(a2+a4)+(a6+a8)+(a10+a12)+(a14+a16)=5+17+29+41=92。
前16项和为540,则a1+a3+a5+a7+a9+a11+a13+a15=448。
当n为奇数时,an+2-an=3n-1。
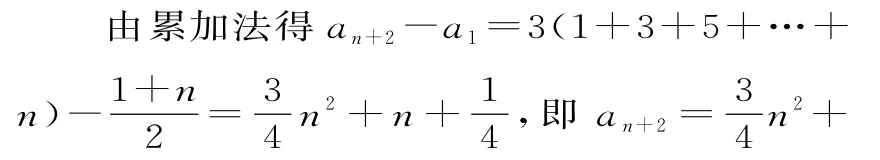
七、考查数列中的最值
此类问题综合性强,综合考查函数与方程、化归与转化的数学思想方法,考查同学们综合运用知识的能力,涉及配方法、均值不等式等知识。
例8【2022 年全国甲卷理数第17题】记Sn为数列{an}的前n项和。已知n=2an+1。
(1)证明:{an}是等差数列;
(2)若a4,a7,a9成等比数列,求Sn的最小值。
解析:(1)(证法1)由已知得2Sn+n2=2nan+n。①
同理,2Sn+1+(n+1)2=2(n+1)an+1+n+1。②
②- ①可 得2an+1=2(n+1)an+1-2nan-2n。
整理得an+1=an+1。
由等差数列定义知{an}为等差数列。(证法2)因为,所以2Sn+n2=2nan+n。
则2Sn+1+(n+1)2=2(n+1)an+1+n+1。
2Sn+1+(n+1)2=2(n+1)(Sn+1-Sn)+n+1。
整理得2nSn+1-2(n+1)Sn=n(n+1)。

解得an=a1+n-1,即an-an-1=1,故数列{an}为等差数列。
故(x+6)2=(x+3)(x+8),解得x=-12,即a1=-12。
所以an=-12+(n-1)×1=n-13。
可得a1<a2<a3<…<a12<0,a13=0,a14>0。
故当n=12或者n=13时Sn取最小值,
因此,Sn的最小值为-78。
(方法2)由(1)可得a4=a1+3,a7=a1+6,a9=a1+8。
又a4,a7,a9成等比数列,所以a27=a4·a9,即(a1+6)2=(a1+3)·(a1+8),解得a1=-12。
则an=n-13,所以Sn= -12n+
当n=12或n=13时,(Sn)min=-78。

