抛物线问题之“一题多解”赏析

■上海市嘉定区安亭高级中学 陈春霞

“一题多解”是一种发散性思维,也是数学解题的最高境界。“一题多解”不仅能建立知识之间的联系,培养数学探究精神,而且能让我们感受到数学的神奇与奥妙,激发对数学的热爱。下面让我们赏析几道抛物线问题的“一题多解”。

一、方程问题

例1设抛物线C:y2=2px(p＞0)的焦点为F,点M在抛物线C上,|MF|=5,若以MF为直径的圆过点A(0,2),则抛物线C的方程为_____。

思路1:设出点M坐标,利用抛物线定义与两条直线垂直得到方程组求解。这里利用了直径所对应的圆周角为直角这一性质。

思路2:由“以MF为直径的圆与y轴相切”,可得圆心纵坐标为2,M点的纵坐标为4,利用焦半径公式求解。

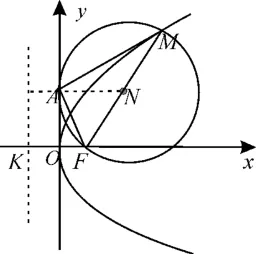
图2

所以y2=4x或y2=16x。

思路3:设出点M的坐标,利用AM,AF的数量积为零,及求解。

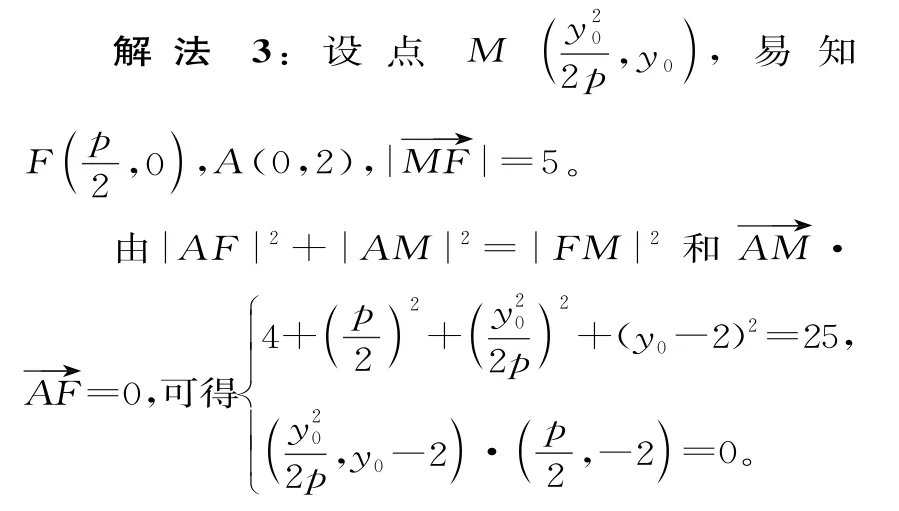
解得y0=4,p=8或p=2,所以y2=4x或y2=16x。

思路4:由直线AO与以MF为直径的圆 相 切 得 到 ∠OAF= ∠AMF,应 用sin ∠OAF=sin ∠AMF求解。

解法4:如图3所示,易知以MF为直径的圆与y轴相切,可得切点A的坐标为(0,2),∠OAF=∠AMF。

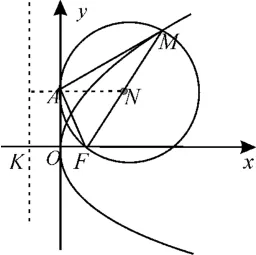
图3

在Rt△AOF中,sin ∠OAF

点评：求圆锥曲线的标准方程,常用待定系数法或利用圆锥曲线的定义。本题解法的实质都是待定系数法,不同之处在于对条件的转化的方向或形式不一样。解法1与解法2主要从代数的角度考虑,侧重于代数的运算,区别在于解法1把直角转化为斜率之积等于-1。解法3 采用了向量法,体现了向量的“工具性”。解法4 应用三角函数的关系求解,建立了几何图形与三角函数之间的联系。

二、最值问题

例2已知抛物线y2=2px(p＞0)的焦点为F,准线为l,A,B是抛物线上两动点,且,设线段AB的中点M在l上的投影为点N,则的最大值为( )。

A.4 B.1 C.2 D.3

思路1:将问题聚焦在三角形中,利用抛物线定义、余弦定理及基本不等式求解。

思路2:将问题聚焦在三角形中,利用抛物线的定义、正弦定理,以及三角函数的有界性求解。

点评：解法1 与解法2 将问题聚焦在三角形中,利用正弦、余弦定理,再利用三角函数的有界性和基本不等式求解,这是处理与三角形有关的最值问题的常用解题策略。

三、定点问题

例3已知抛物线y2=2x上两个动点B,C和定点A(1,- 2),若∠BAC=90°,则直线BC所过的定点的坐标为____。

思路1:设出直线BC的方程x=my+n,及点B,C的坐标,联立方程组,利用韦达定理将条件中的直角利用向量进行坐标转化,求出m,n的关系,进而求解所过的定点。

解法1:设直线BC的方程x=my+n,B(x1,y1),C(x2,y2)。

由x=my+n与y2=2x联立消去x,得y2-2my-2n=0。

所以y1+y2=2m,y1y2=-2n。①

由①②得(y1+y2)(y- 2)=2(x-3),即BC过定点(3,2)。

ii)当直线BC的斜率不存在时,y1+y2=0,亦过点(3,2)。

综上,直线BC过定点(3,2)。

思路3:利用抛物线上两点连线的斜率公式求解。

解法3:设B(x1,y1),C(x2,y2),A(x0,y0)。

由①+ ②,得(y1+y2)(y+y0)-2p(x-x0-2p)=0。

令y+y0=0,x-x0-2p=0,得到定点(x0+2p,-y0),代入A点坐标得定点坐标为(3,2)。

点评：解法1 将直线BC的方程与抛物线方程联立后,利用向量数量积等于0 求出定点坐标,是通法；解法2利用抛物线上两点B(x1,y1),C(x2,y2)连线的斜率公式k=,以及两条直线垂直斜率乘积为-1求解；解法3利用抛物线上两点连线的斜率公式求解。给出一般情况下的解法,同学们以后遇到此类型题目,用两次结论可以提高解题速度和准确度。