函数恒(能)成立之导数解法
■江苏省盐城市明达高级中学 张 冉
“不等式恒(能)成立问题”是高考的热点题型,频繁出现在历年的高考中,这类题把不等式、函数、导数等内容有机地结合起来,因其覆盖知识点多,综合性强,解法灵活等特点而备受高考、竞赛命题者的青睐。用导数解决不等式“恒成立”“能成立”或“存在性”问题的常用方法是分离参数,分类讨论或构造新函数等,将不等式问题转化为函数的最值问题。下面从几个方面剖析函数恒(能)成立之导数解法。
一、分离参数法求参数范围
例1已知函数f(x)=ex-x-1,若f(x)≤x2+(a-1)x在x∈(0,+∞)内有解,求实数a的取值范围。

又f'(x)=ex-1,当x>0时,f'(x)>0,f(x)=ex-x-1 在(0,+∞)上单调递增,且f(0)=0,故ex-x-1>0。所以当0<x<1 时,g'(x)<0,g(x)单调递减;当x>1时,g'(x)>0,g(x)单调递增。因此,g(x)≥g(1)=e-2,即a≥e-2。
点评:分离参数法求范围:若f(x)≥a或g(x)≤a能成立,只需满足f(x)max≥a或g(x)min≤a即可,求出f(x)的最大值或g(x)的最小值,从而解决问题。
二、分类讨论法求参数范围
例2已知函数f(x)=(x-1)·ln(x-2)-a(x-3),a∈R。
(1)若a=1,讨论f(x)的单调性;
(2)当x>3 时,若f(x)>0 恒成立,求a的取值范围。
解析:(1)f(x)的定义域为(2,+∞)。当a=1时,f(x)=(x-1)ln(x-2)-x+3。
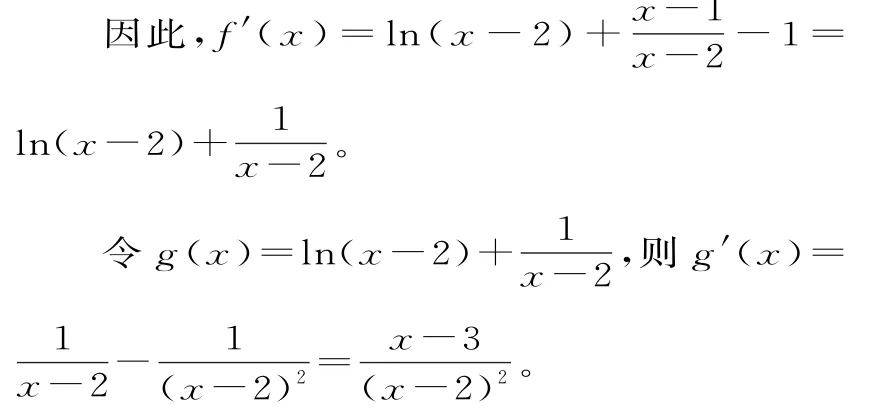
令g'(x)=0,解得x=3。
当x∈(2,3)时,g'(x)<0,g(x)单调递减;
当x∈(3,+∞)时,g'(x)>0,g(x)单调递增。
所以,g(x)min=g(3)=1>0,则g(x)=f'(x)>0对任意的x>2恒成立。
函数f(x)的单调递增区间为(2,+∞),无递减区间。
(2)当x>3时,f(x)>0恒成立等价于在(3,+∞)上恒成立。

令φ(x)=x2-2(a+1)x+4a+1(x>3),则φ(x)图像为开口向上,对称轴为x=a+1的抛物线的一部分。
①当a≤2 时,a+1≤3,φ(x)在(3,+∞)上单调递增,且φ(3)=4-2a≥0。
所以,φ(x)≥0,即h'(x)≥0,故函数h(x)在(3,+∞)上单调递增。
又h(3)=0,所以h(x)>0在(3,+∞)上恒成立,满足题意。
②当a>2时,a+1>3,φ(3)=4-2a<0,所以方程φ(x)=0 有两个相异实根。设为x1,x2,且x1<x2,则x1<3<x2。
当x∈(3,x2)时,φ(x)<0,h'(x)<0,h(x)在(3,x2)上单调递减。
又因为h(3)=0,所以当x∈(3,x2)时,h(x)<h(3)=0,h(x)>0 在(3,+∞)上不恒成立,不满足题意。
综上,a的取值范围为(-∞,2]。
点评:本题考查利用函数解决不等式恒成立求参数的取值范围,不便于分离参数。注意到h(3)=0,由此对实数a的取值进行分类讨论,将问题转化为考查函数h(x)在(3,+∞)上的单调性,只需对实数a的取值进行分类讨论,结合单调性来求解。
三、拆解法求参数的取值范围
例3已知函数f(x)=ex-ax+2(e为自然对数的底数)。
(1)若a=2,求f(x)的单调区间;
(2)设g(x)=ex+e-x,若对任意x∈R,均存在x0∈[-1,2],使得f(x)>g(x0),求实数a的取值范围。
解析:(1)若a=2,f(x)=ex-2x+2,则f'(x)=ex-2。
令f'(x)=ex-2>0,得x>ln 2;
令f'(x)=ex-2<0,得x<ln 2。
所以f(x)在(-∞,ln 2)上单调递减,在(ln 2,+∞)上单调递增。
(2)由题意可知,即求f(x)>g(x0)min成立的a的取值范围。
因为g(x)=ex+e-x,x∈[-1,2],所以,当且仅当x=0时取等号。
故g(x0)min=2,即求f(x)=ex-ax+2>2对任意x∈R 成立的a的取值范围。
当a<0 时,f'(x)=ex-a>0,此时f(x)在R 上单调递增,且,不满足f(x)min>2。当a=0时,易知f(x)>2,显然成立。
当a>0 时,令f'(x)=ex-a>0,得x>lna;令f'(x)=ex-a<0,得x<lna。
故f(x)在(-∞,lna)上单调递减,在(lna,+∞)上单调递增。
f(x)min=f(lna)=a-alna+2。
则a-alna+2>2,解得0≤a<e。
综上,实数a的取值范围为[0,e)。
例4已知函数f(x)=xex,g(x)=- (x+1)2+a,若∃x1,x2∈R,使 得f(x2)≤g(x1)成立,则实数a的取值范围是( )。

解析:∃x1,x2∈R,使得f(x2)≤g(x1)成立,则f(x)min≤g(x)max。
由题意得f'(x)=ex+xex=(x+1)ex。
所以函数f(x)在(-∞,-1)上单调递减,在(-1,+∞)上单调递增,f(x)min=
由题意得g(x)max=g(-1)=a,则a≥,选C。
点评:“双变量”的恒(能)成立问题可以拆解求参数,进行等价变换,常见的拆解转换有:(1)∀x1,x2∈D,f(x1)>g(x2)⇔f(x)min>g(x)max;
(2)∀x1∈D1,∃x2∈D2,f(x1)>g(x2)⇔f(x)min>g(x)min;
(3)∃x1∈D1,∀x2∈D2,f(x1)>g(x2)⇔f(x)max>g(x)max。
四、同构变形、构造函数求参数的取值范围
例5(2023年山东省部分学校联考)已知函数f(x)=aeax-lnx,对任意的x>1,f(x)≥0恒成立,则a的取值范围是_____。
解析:当a≤0时,f(x)<0不符合题意。当a>0 时,则aeax≥lnx,即axeax≥xlnx⇔eaxln eax≥xlnx。
设g(x)=xlnx(x>1),则g'(x)=lnx+1>0恒成立,故g(x)在(1,+∞)上单调递增。
因为x>1,a>0,所以eax>1。

点评:求解不等式恒(能)成立问题时,要注意对不等式进行合理的变形,便于构造函数后求导研究其性质,合理的等价转化往往可以达到事半功倍的效果。
总之,逻辑关系是数学推理的本质,处理函数中任意性与存在性问题,要学会从不同的角度、不同的方向加以分析探讨, 认清逻辑关系,熟练掌握分离参数法、数形结合、分类讨论等常用的方法,巧妙转化为“能成立”与“恒成立”问题,从而能在解题时选取恰当的解法,触类旁通。只有这样“明辨、清源”,同学们才能在考试过程中实现“水源不断,活水常来”。
变式训练
1.已知函数f(x)=lnx-ax(a是常数),若∀x>0,f(x)<0,则实数a的取值范围_____。
解析:因为∀x>0,f(x)<0,所以lnx-ax<0恒成立,即

易得当x∈[1,e]时,lnx-2x+1<0,且2lnx-x-1<0,从而F'(x)<0,所以F(x)在[1,e]上单调递减。
于是a>F(x)min=F(e)=-1-e。
故a的取值范围为(-1-e,+∞)。

f(x)max≤g(x)max,解 得m∈

