一元函数的导数及其应用单元测试卷(A 卷)参考答案与提示
一、单选题
1.B 2.D 3.C 4.A 5.C 6.D
7.A 提示:f'(x)=5x4+an+1cosx-(2an+3),易知函数f'(x)为偶函数。
又f'(x)有唯一零点,则必有f'(0)=an+1-(2an+3)=0,即an+1=2an+3。
整理得an+1+3=2(an+3)。
所以数列{an+3}是以2为公比的等比数列。又a1=1,则an+3=4×2n-1,an=2n+1-3。
所以a10-a4+a2=2 045-29+5=2 021。
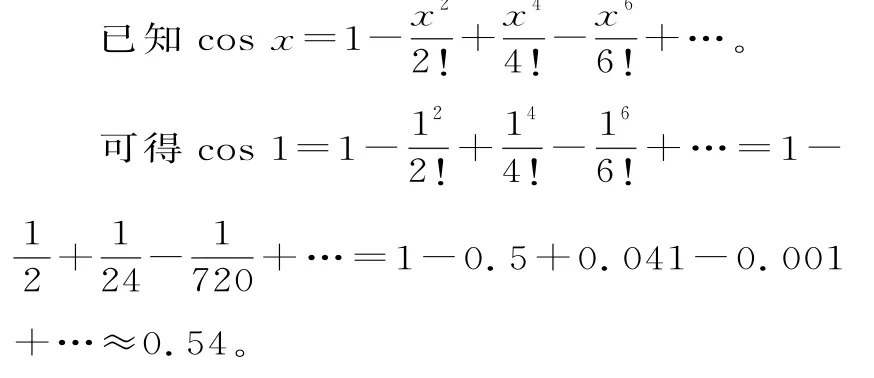
所以cos 1-1≈-0.46。
二、多选题

所求不等式的整数解为1或2。
当x=1时取得最大值
当x=e时取得最大值
作出两个函数的图像,如图1所示。
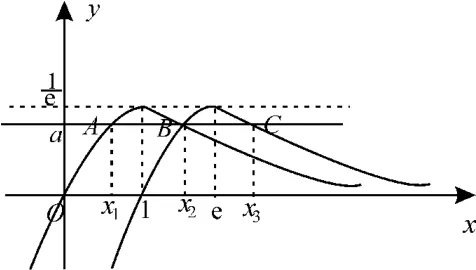
图1
由,得x2=aex2,故选项A 正确。
11.BC 提示:对于A 选项,构造函数g(x)=f(x)+x=xlnx+x,定义域为(0,+∞),则g'(x)=lnx+2。

对于D 选项,当a=0时,方程f(x)=0只有一个根x=1,D 选项错误。
12.ABC 提示:已知f(x)=f(2)+f(4-x),令x=2,则f(2)=f(2)+f(2),解得f(2)=0。
所以f(x)=f(4-x),函数f(x)的图像关于直线x=2对称,A 正确。
因为f(x-2 024)+f(2 024-x)=0,所以f(x)+f(-x)=0,f(x)为奇函数。
则f'(x)-f'(-x)=0,即g(-x)=f'(-x)=f'(x)=g(x),故g(x)为偶函数,B正确。
由f(x)=f(4-x)得,f'(x)=-f'(4-x),即g(x)=-g(4-x),所以g(x)的图像关于(2,0)对称,且g(2)=0。
又因为g(x)为偶函数,所以g(4-x)=g(x-4)。
g(x)=-g(4-x)=-g(x-4),则g(x)=g(x-8),g(x)是以8为周期的周期函数,故g(2 022)=g(-2)=g(2)=0。C正确。
因为f(x)=f(4-x)=-f(x-4),所以f(x)=f(x-8),f(x)是以8 为周期的周期函数。
所以f(2 023)=f(-1)=-f(1)=-2 023,D 错 误。
三、填空题
13.2 提示:已知等式两边同时乘以x整理 得,2xf(x)+x2f'(x)=2x2cos 2x+2xsin 2x+2x,即[x2f(x)]'=(x2sin 2x+x2)'。
故x2f(x)=x2sin 2x+x2+c。
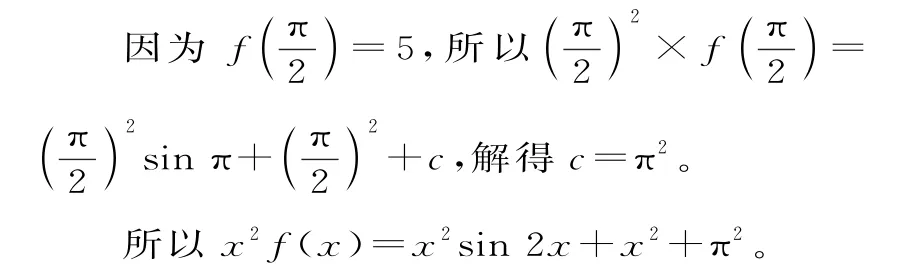
当x=π时,π2f(π)=π2×sin 2π+π2+π2,解得f(π)=2。
14.0 提示:因为正实数x,y满足ex=ylnx+yln
y=yln(xy),所 以xex=xyln(xy)=eln(xy)·ln(xy)。
构造函数f(x)=xex,则f(x)=f(ln (xy)),f'(x)=(x+1)ex。
当x>0时,f'(x)>0,函数f(x)在(0,+∞)上单调递增。
故f(x)=f(ln(xy))⇔x=ln(xy)。

ax2-(2a+1)x,函数定义域为R,可得f'(x)=ex-1+2ax-(2a+1)。
易知f'(1)=1+2a-(2a+1)=0。
不妨设g(x)=ex-1+2ax-(2a+1),函数定义域为R,可得g'(x)=ex-1+2a。
①当2a≥0时,g'(x)>0恒成立,g(x)在R 上单调递增,所以函数f'(x)=ex-1+2ax-(2a+1)在R 上单调递增。
当x<1时,f'(x)<0,f(x)单调递减;当x>1时,f'(x)>0,f(x)单调递增。所以x=1是f(x)的极小值点,不符合题意。
②当a<0时,令g'(x)=ex-1+2a=0,解得x=1+ln (-2a)。
当x<1+ln (-2a)时,g'(x)<0,g(x)单调递减;当x>1+ln (-2a)时,g'(x)>0,g(x)单调递增。
故f'(x)min=f'(0)+ln(-2a)。
又f'(1)=0,且x=1不是f(x)的极值点,所以1+ln (-2a)=1,解得

当t>1 时,u'(t)>0,函数u(t)在(1,+∞)上单调递增;
当0<t<1 时,u'(t)<0,函数u(t)在(0,1)上单调递减。
故当t=1时,函数u(t)取得极小值即最小值,u(1)=2>0,h'(t)>0恒成立。
故函数h(t)在t∈(0,+∞)上单调递增。
又原不等式等价于h(e2kx)≥h(x2),则e2kx≥x2,即2kx≥2lnx,也即恒成立。
四、解答题
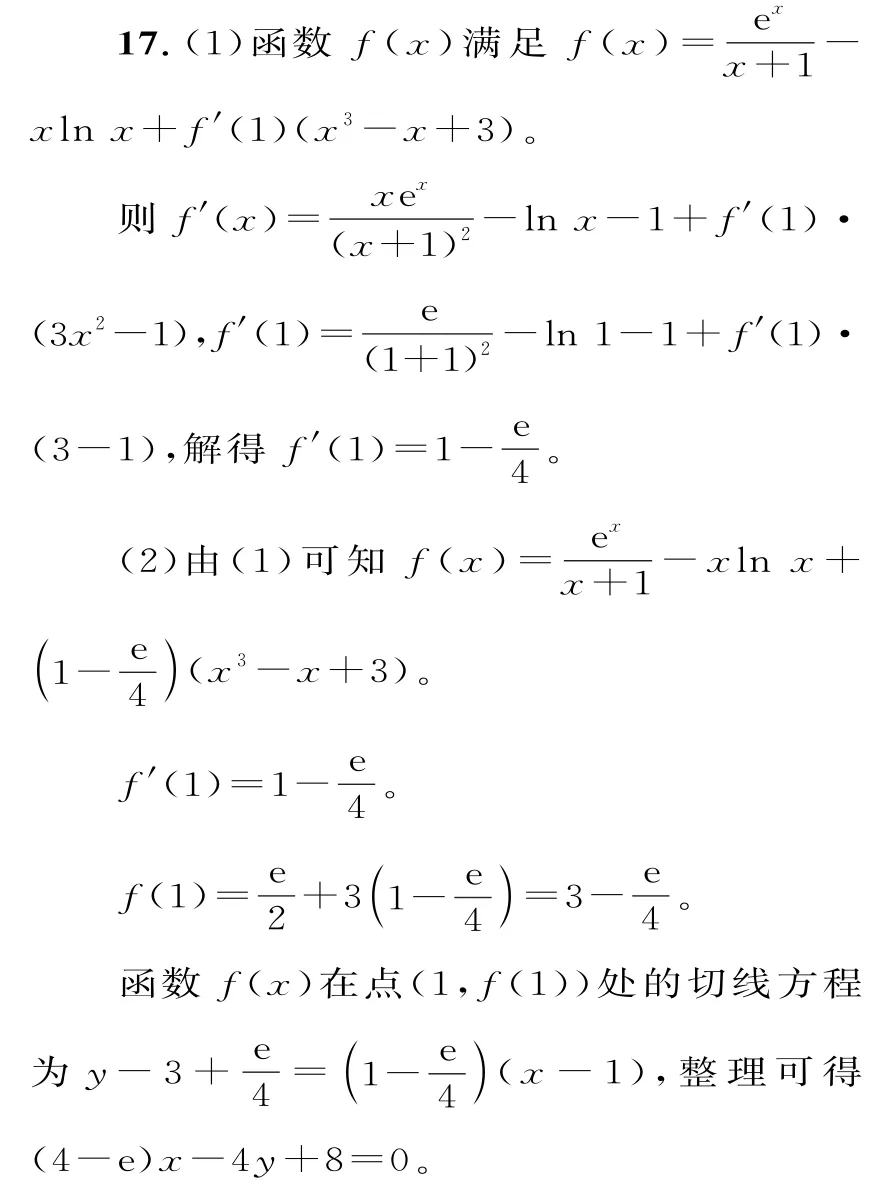
18.设矩形在第一象限的顶点坐标为(x0,y0),根据矩形和椭圆的对称性可得,将该矩形绕y轴旋转一周得到的圆柱体的母线长l=2y0,底面圆的半径r=x0。

a的取值范围是(2e-2,+∞)。
21.(1)f(x)=ax-xlnx的定义域为(0,+∞),f'(x)=a-1-lnx。
令f'(x)=0,得x=ea-1。
当x∈(0,ea-1)时,f'(x)>0,f(x)单调递增;
当x∈(ea-1,+∞)时,f'(x)<0,f(x)单调递减。
①当ea-1≤1(即a≤1)时,f(x)在[1,e]上单调递减,f(x)max=f(1)=a。
②当ea-1≥e(即a≥2)时,f(x)在[1,e]上单调递增,f(x)max=f(e)=ae-e。
③当1<ea-1<e(即1<a<2)时,f(x)在[ea-1,e]上单调递减,f(x)在[1,ea-1]上单调递增。
所以f(x)max=f(ea-1)=aea-1-ea-1·(a-1)=ea-1。
(2)由(1)知在(0,+∞)上,f(x)max=f(ea-1)=ea-1。
设g(a)=f(ea-1)-a=ea-1-a。
由题意,应使g(a)≤0,g'(a)=ea-1-1。令g'(a)=0,得a=1。
所以当a∈(-∞,1)时,g'(a)<0,g(a)单调递减;
当a∈(1,+∞)时,g'(a)>0,g(a)单调递增。
g(a)min=g(1)=0。
所以使g(a)≤0的实数a只有a=1。
22.(1)依题意知,x1,x2(0<x1<x2)是函数y=f(x)的两个零点。
设x2=tx1,因x2>x1>0,故t>1。

(2)因曲线C:y=m-kx2与曲线y=f(x)有唯一的公共点,故方程m-kx2=2lnx-x有唯一解,即方程kx2+2lnx-x=m有唯一解。
令g(x)=kx2+2lnx-x,x>0,则
当1-16k≤0,即时,g'(x)≥0,函数y=g(x)单调递增。
易知g(x)与y=m有且只有一个交点,满足题意。

故两根一个大于4,一个小于4,此时函数g(x)先增后减再增,存在一个极大值和一个极小值。
要使kx2+2lnx-x=m有唯一实数根,则m大于g(x)的极大值或小于极小值。

综上,要使对∀k>0,曲线C:y=mkx2与曲线y=f(x)都有唯一的公共点,m的取值范围为[4ln 2-3,+∞)。

