利用导数的几何意义的常见题型

■安徽省安庆市洪汪宝名师工作室 洪汪宝

可导函数y=f(x)的图像在点(x0,f(x0))处切线的斜率等于f'(x0)就是导数的几何意义,于是可得到可导函数y=f(x)的图像在点(x0,f(x0))处的切线方程为y-f(x0)=f'(x0)(x-x0),求解时抓住切点在函数y=f(x)的图像上,又在切线上,切点处的导数值即为切线斜率这三点即可处理与切线有关的问题。下面结合具体例题归纳利用导数的几何意义的常见题型。

一、求切线方程

1.1求在某点处的切线方程

1.2求过某点的切线方程

整理得(x0+1)(x0-2)2=0,则x0=-1或x0=2。

故所求切线的方程为4x-y-4=0 或x-y+2=0。

点评：注意在某点处的切线与过某点的切线的区别：在某点处的切线,该点是切点,一定在函数y=f(x)的图像上；过某点的切线,该点不一定是切点,该点可能在函数y=f(x)的图像上,也可能不在。

二、已知切线求参数值(或范围)

例3已知曲线y=ax3与直线6xy-4=0相切,则实数a的值为____。

解析:设切点为(m,n),由y=ax3得y'=3ax2。由题意得解得m=1,n=2,a=2。

例4若直线y=2x+b是曲线y=2alnx的切线,且a＞0,则实数b的最小值是____。

解析:y=2alnx的导数为由于直线y=2x+b是曲线y=2alnx的切线,设切点为(m,n),则又2m+b=2alnm,故b=2alna-2a(a＞0)。

令h(a)=2alna-2a,h'(a)=2(lna+1)-2=2lna。当a＞1时,h'(a)＞0,h(a)单调递增;当0＜a＜1时,h'(a)＜0,h(a)单调递减。a=1 为极小值点,也为最小值点,故h(a)的最小值为2ln 1-2=-2。

点评：已知切线求参数值(或范围),一般先设出切点,利用导数的几何意义求出切线方程,并与已知的切线方程进行对比,即可建立方程,从而得解。

三、切线条数问题

3.1判断切线条数

例5已知曲线S:y=3x-x3,则过点P(2,2)可向曲线S引切线,其切线条数为( )。

A.1 B.2 C.3 D.0

解析:设在曲线S上的切点为(t,3tt3)。已知y=3x-x3,则y'=3-3x2。

所以曲线S在点(t,3t-t3)处的切线方程为y-(3t-t3)=(3-3t2)(x-t)。

将点P(2,2)的坐标代入切线方程得t3-3t2+2=0,即(t-1)(t2-2t-2)=0。

解得t1=1,t2=1+ 3,t3=1- 3。

因此过点P(2,2)可向曲线S引3条切线,选C。

3.2已知切线条数求参数值(或范围)

例6已知过点M(m,0)作曲线C:y=x·lnx的切线有且仅有两条,则实数m的取值范围是____。

解析:由题意可知,曲线C:y=x·lnx,定义域为(0,+∞),则y'=lnx+1。

设切点为(x0,y0),则切线斜率k=lnx0+1,切线方程为y-y0=(lnx0+1)·(x-x0)。将M(m,0)代入切线方程得-y0=(lnx0+1)(m-x0)。

又因为y0=x0·lnx0,所以mlnx0+m-x0=0。

显然m≠0,整理得

由于过点M(m,0)作曲线C:y=x·lnx的切线有且仅有两条,即有两个解。

所以当x∈(0,1)时,g'(x)＞0,g(x)单调递增;当x∈(1,+∞)时,g'(x)＜0,g(x)单调递减。所以g(x)max=g(1)=1。

所以实数m的取值范围是(1,+∞)。

点评：设出切点,利用导数的几何意义求出切线方程,因切线过已知点,得到关于切点横坐标的方程,切线有几条转化为方程有几个解。例5直接解三次方程,如果方程不便求解,可转化为判断函数有几个零点；例6直接转化为两个函数图像交点有两个时求参数的取值范围,注意分离参数。

四、公切线问题

4.1求公切线方程

例7已知直线l是曲线f(x)=ln(x+1)和曲线g(x)=ln(e3x)的公切线,则直线l的方程是____。

解析:设直线l的方程为y=kx+b,设直线l与曲线f(x)=ln(x+1)相切于点A(x1,y1),直线l与曲线g(x)=ln(e3x)相切于点B(x2,y2)。

已知f(x)=ln(x+1),则f'(x)=

联立①②可得k-lnk-1=2-lnk,解得k=3,b=2-ln 3。

故直线l的方程是y=3x+2-ln 3。

4.2已知公切线求参数范围

例8已知直线l为曲线y=x+1+lnx在A(1,2)处的切线,若直线l与二次曲线y=ax2+(a+2)x+1 也相切,则a=( )。

A.0 B.-4 C.4 D.0或4

解析:因为y=x+1+lnx,所以y'=

因此,曲线y=x+1+lnx在A(1,2)处的切线斜率k=2。

故曲线y=x+1+lnx在A(1,2)处的切线方程为y-2=2x-2,即y=2x。

由于直线l与曲线y=ax2+(a+2)x+1也相切,故:

可得ax2+ax+1=0。

又a≠0,两线相切有一切点,所以Δ=a2-4a=0,解得a=4 或a=0(舍去)。选C。

例9直线y=kx+b与曲线y=f(x)相切也与曲线y=g(x)相切,则称直线y=kx+b为曲线y=f(x)和曲线y=g(x)的公切线。已知函数f(x)=x2,g(x)=alnx,其中a≠0,若曲线y=f(x)和曲线y=g(x)的公切线有两条,则a的取值范围为( )。

A.a＜0 B.a＜-1

C.0＜a＜2e D.

解析:设曲线f(x)=x2的切点为(s,s2),则f(x)=x2⇒f'(x)=2x,所以过该切点的切线斜率为f'(s)=2s。因此过该切点的切线方程为y-s2=2s(x-s)⇒y=2sxs2。

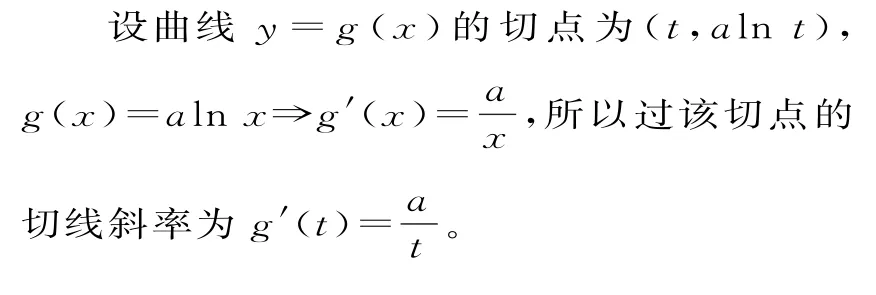
当t＞ e 时,h(t)＜0,当0＜t＜e,h(t)＞0,函数的图像大致如图1所示。

图1

若曲线y=f(x)和曲线y=g(x)的公切线有两条,则a的取值范围为0＜a＜2e。选C。

4.3已知存在公切线,研究切点性质

例10已知函数f(x)=x2+1,g(x)=lnx,若曲线y=f(x)与y=g(x)的公切线和曲线y=f(x)切于点(x1,y1),则x21-ln(2x1)=。

因此,x21-ln(2x1)=2。

点评：解决公切线问题,若在两个函数图像公共点处有公切线,则利用公共点处的函数值相等与导数值相等即可；若切点不同,则分别设出切点,求出两个切线方程,因为是公切线,对比两条切线方程,对应系数分别相等即可建立方程。

五、切线的应用

5.1求距离

例11点A在直线y=x上,点B在曲线y=lnx上,则|AB|的最小值为( )。

解析:设平行于直线y=x的直线y=x+b(b≠0)与曲线y=lnx相切。

则两条平行线间的距离即为|AB|的最小值。设直线y=x+b与曲线y=lnx的切点为(m,lnm),则由切点在直线y=x+b上可得lnm=m+b,由切线斜率等于切点处的导数值可得,联立解得m=1,b=-1。

由平行线间的距离公式可得|AB|的最小值为,选A。

例12已知a-lnb=0,c-d=1,求(a-c)2+(b-d)2的最小值____。

解析:依题意得a=lnb,d-c+1=0。

则(b,a)是曲线y=lnx上的点,(d,c)是直线x-y+1=0上的点。

所以(a-c)2+(b-d)2可看成曲线y=lnx上的点到直线x-y+1=0上点的距离的平方。

直线x-y+1=0 的斜率为1,由y=

点(1,0)到直线x-y+1=0 的距离为

因此(a-c)2+(b-d)2的最小值为(2)2=2。

点评：例11 与例12 中两点间的距离直接不好求,结合函数图像利用数形结合转化为两条平行线间的距离,注意利用导数的几何意义求出切线方程,问题即可迎刃而解。

5.2方程问题

例13已知方程有且仅有两个不同的实数解θ,φ(θ＞φ),则以下有关两根关系的结论正确的是( )。

A.cosφ=φsinθ

B.sinφ=-φcosθ

C.cosθ=θcosφ

D.sinθ=-θsinφ

分别作出y=|cosx|,y=kx的图像。

由图2可知,y=kx与y=-cosx相切时符合题意。

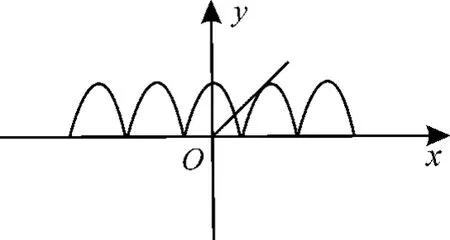
图2

设f(x)=-cosx, 则f'(x)=sinx。

因为θ＞φ,所以θ为切点横坐标,且φ是直线y=kx与y=cosx交点的横坐标。

因为切线过原点,所以切线斜率k=,选A。

5.3恒成立问题

例14已知函数f(x)=ax+lnx+1-xe2x对任意的x＞0,f(x)≤0恒成立,则实数a的取值范围为( )。

A.(-∞,0] B.(-∞,2]

C.(-∞,1] D.(-∞,3]

解析:函数y=ex在点(0,1)处的切线方程为y=x+1。

构造函数g(x)=ex-x-1,对其求导得g'(x)=ex-1。于是,当x∈(-∞,0)时,g'(x)＜0,函数g(x)单调递减;当x∈(0,+∞)时,g'(x)＞0,函数g(x)单调递增。所以当x=0 时,g(x)min=g(0)=0,因此ex≥x+1。

于是f(x)=ax+lnx+1-xe2x=ax+lnx+1-e2x+lnx≤ax+lnx+1-(2x+lnx+1)=(a-2)x≤0恒成立,所以a-2≤0,解得a≤2,选B。

点评：借助切线进行整体放缩简化了整个求解过程,注意利用对数恒等式b=alogab(a＞0 且a≠1,b＞0)进行变形,同时注意ex≥x+1,ex-1≥x,ex≥ex,x-1≥lnx等重要不等式的积累与应用。

5.4证明不等式

例15已知函数f(x)=x3-x,设a＞0,如果过点(a,b)可作曲线y=f(x)的三条切线,求证:-a＜b＜f(a)。

证明:设切点为(t,t3-t),对函数求导得f'(x)=3x2-1。

于是得切线方程为y-(t3-t)=(3t2-1)(x-t),整理得y=(3t2-1)x-2t3。

又因为切线过点(a,b),所以b=(3t2-1)a-2t3。

因为过点(a,b)可作曲线y=f(x)的三条切线,则方程2t3-3at2+a+b=0有三个相异的实数根。

记g(t)=2t3-3at2+a+b,则g'(t)=6t2-6at=6t(t-a)。

当t变化时,g(t),g'(t)的变化情况如表1所示。

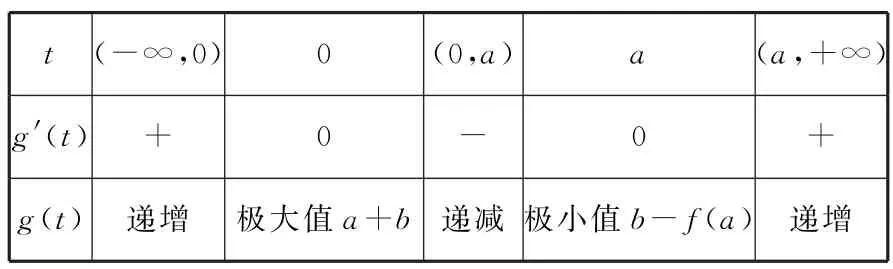
表1

由g(t)的单调性知,当极大值a+b＜0或极小值b-f(a)＞0时,方程g(t)=0 最多有一个实根;

当a+b=0 时,解方程g(t)=0 得t=,即方程g(t)=0只有两个相异的实数根;

当b-f(a)=0时,解方程g(t)=0得t,即方程g(t)=0只有两个相异的实数根。

综上,如果过(a,b)可作曲线y=f(x)的三条切线,即g(t)=0有三个相异的实数根,则即-a＜b＜f(a),得证。

例16已知函数f(x)=aex-lnx-1,证明:当时,f(x)≥0。

证明:构造函数g(x)=ex-x-1,对其求导得g'(x)=ex-1。

于是,当x∈(-∞,0)时,g'(x)＜0,函数g(x)单调递减;当x∈(0,+ ∞)时,g'(x)＞0,函数g(x)单调递增。

所以当x=0时,g(x)min=g(0)=0。

因此,ex≥x+1,于是ex-1≥x。

同时g(lnx)≥0,可得x≥lnx+1。

点评：例15中的切线有三条转化为方程有三个根,再转化为三次函数图像与x轴有三个不同的交点,分析其极大值与极小值即可得到所要证明的不等式；例16借助切线进行两次放缩,技巧性比较强,对同学们分析问题和解决问题的能力要求比较高。