一元函数的导数及其应用单元测试卷(A 卷)

■四川省广安市广安友实学校 孟召臣

一、单选题(本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。)

1.下列四个函数中,在区间[0,1]上的平均变化率最大的为( )。

A.y=xB.y=ex

C.y=sinxD

2.当x＞0 时,可导函数f(x)满足:则f'(x)=( )。

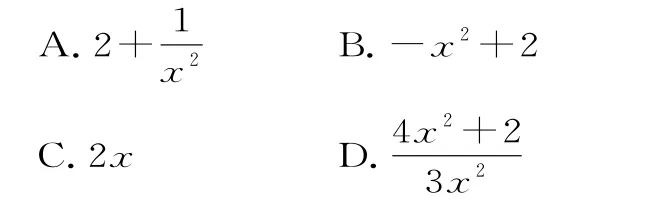
3.已知函数f(x)=(x2-a)ex,则“a≥-1”是“f(x)有极值”的( )。

A.充分不必要条件

B.充要条件

C.必要不充分条件

D.既不充分也不必要条件

4.近几年,出现了一些网络流行语,如“yyds”“内卷”“躺平”等,现定义方程f(x)=f'(x)的实数根x叫做函数f(x)的“躺平点”。若函数g(x)=ex-x,h(x)=lnx,φ(x)=1 024x+1 024的“躺平点”分别为a,b,c,则a,b,c的大小关系为( )。

A.b＞a＞cB.a＞b＞c

C.c＞a＞bD.c＞b＞a

5.拉格朗日中值定理是微分学的基本定理之一,内容为:如果函数f(x)在闭区间[a,b]上的图像连续不间断,在开区间(a,b)内的导数为f'(x),那么在区间(a,b)内至少存在一点c,使得f(b)-f(a)=f'(c)(b-a)成立,其中c叫做f(x)在[a,b]上的“拉格朗日中值点”。根据这个定理,可得函数f(x)=lnx在[1,e]上的“拉格朗日中值点”为( )。

A.2 021 B.2 022

C.2 023 D.[1,+∞)

7.在数列{an}中,a1=1,且函数f(x)=x5+an+1sinx-(2an+3)x+3 的 导 函 数 有唯一零点,则a10-a4+a2的值为( )。

A.2 021 B.2 022

C.2 023 D.2 024

A.0.50 B.-0.46

C.-0.54 D.0.56

二、多选题(本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5 分,部分选对的得2分,有选错的得0分。)

9.已知函数y=f(x)满足:f(1)=1,且f(x)在R 上 的 导 数,则不等式的整数解可以为( )。

A.4 B.3 C.2 D.1

10.已知直线y=a与曲线相交于A,B两点,与相交于B,C两点,A,B,C的横坐标分别为x1,x2,x3,则( )。

A.x2=aex2B.x2=lnx1

C.x3=ex2D.x1x3=

11.已知函数f(x)=xlnx,若0＜x1＜x2,则下列选项正确的是( )。

A.x1+f(x1)＜x2+f(x2)

B.x2f(x1)＜x1f(x2)

D.若方程f(x)=a有一个根,则

12.已知定义在R 上的可导函数f(x),记g(x)=f'(x)为f(x)的导函数。若f(x-2 024)+f(2 024-x)=0,且f(x)=f(2)+f(4-x),f(1)=2 023,则下列说法正确的是( )。

A.f(x)的图像关于x=2对称

B.g(x)为偶函数

C.g(2 022)=0

D.f(2 023)=2 023

三、填空题(本题共4小题,每小题5分,共20分。)

15.函数f(x)=ex-1+ax2-(2a+1)x(其中a为实数),若x=1不是f(x)的极值点,则a=_____。

四、解答题(本题共6小题,共70分,解答时应写出文字说明、证明过程或演算步骤。)

17.(本小题10分)已知函数f(x)满足

(1)求f'(1)的值;

(2)求这个函数f(x)在点(1,f(1))处的切线方程。

18.(本小题12分)已知在直角坐标系xOy中矩形的四个顶点都在椭圆C上,将该矩形绕y轴旋转一周,得到一个圆柱体,当该圆柱体的体积最大时,求该圆柱体的侧面积。

(1)求函数f(x)的零点及单调区间;

20.(本小题12 分)已知函数f(x)=e2x-2x-1。

(1)证明:f(x)≥0。

(2)∃x0∈(0,+∞),使得f(x0)＜ax0-1成立,求a的取值范围。

21.(本小题12 分)已知函数f(x)=ax-xlnx。

(1)讨论f(x)在[1,e]上的最大值。

(2)是否存在实数a,使得对任意x＞0,都有f(x)≤a? 若存在,求a的取值范围;若不存在,说明理由。

22.(本小题12 分)已知函数f(x)=alnx-x,e是自然对数的底数。

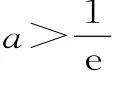
(1)若x1,x2(0＜x1＜x2)是函数y=f(x)的两个零点,证明:

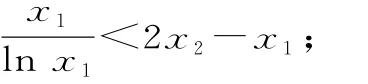
(2)当a=2时,若对于∀k＞0,曲线C:y=m-kx2与曲线y=f(x)都有唯一的公共点,求实数m的取值范围。