课堂教学由“有效”走向“高效”的策略探讨

⦿ 江苏省扬州市广陵区李典学校 陈晶晶

如何使课堂由“有效”走向“高效”是一个持久不变的热门话题.在初中数学课堂上,若想实现由“有效”走向“高效”这一目标,教师应以发展学生为目标,认真研究教材,研究教学,充分挖掘各种有价值的教学资源,让学生通过经历思考、探索、交流、归纳等活动实现认知结构的优化,以此提升教学质量和学习品质,提高课堂教学效率.

1 引导举一反三

在传统课堂教学模式下,部分教师认为只有讲得多、讲得细,学生才能学得多、学得快、学得好,为此他们常常将初中数学课堂打造成“满堂灌”的课堂.实际上,以师为中心的教学模式将学生变成了被动的接受者,容易造成学生惰性思维,使他们在解题中常常出现“懂而不会”的情况,进而影响“举一反三”能力的提升.要改变这一现状,教师应该多提供一些机会让学生自己去思考、去体验、去探究,自主发现知识间的内在联系,揭示数学的本质,从而培养独立思考和“举一反三”的能力.

例1在数据0,3,6,2,0,2,1,2,3中,众数是______.

例1是基础题,学生只要掌握众数的概念就能轻松解决.教学中,若仅教会学生解题,只能称得上有效教学.为了实现从“有效”到“高效”的过渡,教师还可以在此基础上继续提问,让学生思考平均数、中位数、极差、方差和标准差.通过有效的引导,学生能够在理解众数的基础上,举一反三,掌握平均数、中位数等相关知识.由此及彼的探究,有利于知识体系的建构,从而推动课堂教学由“有效”向“高效”转变.

在解题教学中,教师不要局限于“就题论题”式的讲授,应启发学生举一反三,引导学生将解题的方法迁移到相似的题目中,以此提高解题能力.

2 关注一题多解

众所周知,数学题目是灵活多变的,同一问题往往可能有多种解题方法.因此,在日常教学中,教师要鼓励学生从不同角度思考问题,引导学生自主探求解决问题的方法.对于同一问题,若思考的角度不同,解法也会有所不同.当然,教学中教师既要提供时间和空间让学生探寻多种解题路径,也要引导学生解后反思,通过思考“为什么这样解?”“还可以怎样解?”“哪种方法最方便?”等问题发展学生数学思维能力,提高解题效率.

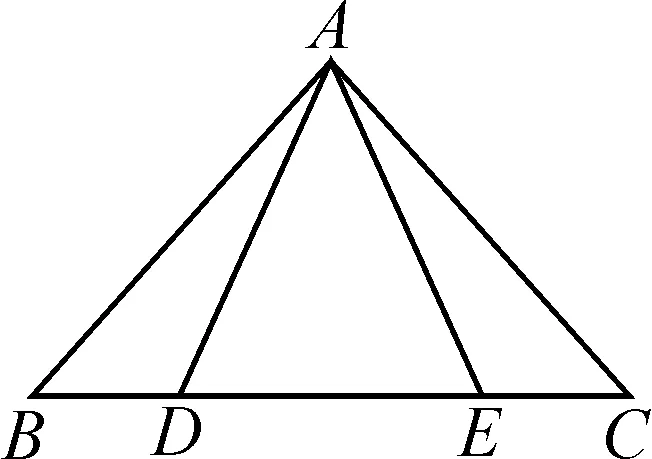
图1

例2如图1,点D,E在三角形ABC的边BC上,其中AB=AC,AD=AE,求证：BD=CE.

本题难度不大,但是证法灵活.不过,部分教师并没有鼓励和指导学生探寻多种证法,仅仅呈现个别学生给出的“标准答案”就草草了事,这样就错失了培养学生发散性思维能力的机会.其实,教师可以引导学生通过独立思考与合作探究相结合的方式探寻多种解决问题的方法,以此积累解题经验,提升数学素养.基于此,学生给出解题思路后,教师可追问：还有其他方法吗?由此通过追问,有效引导学生多向思维,发现多种证法.本题可以应用如下思路来证明：

思路1：根据已知易发现,图1中有两个等腰三角形,于是联想应用“三线合一”的性质来证明.这样通过作底边的中线、高线和顶角平分线,就可以得到3种证法.

思路2：从证明三角形全等的角度出发,可以通过证明△ABD≌△ACE或△ABE≌△ACD来解决问题.证明全等的方法较多,如“AAS,ASA,SAS”等,由此可以得到多种证法.

思路3：从对称的角度出发,利用折叠法证明.

可见,通过多角度探究,学生可以找到不同的证明方法,充分展示了证明角相等或线段相等的一般方法.这样通过引导多向思维,不仅可以实现“双基”的巩固,而且可以提升学生数学学习的热情,有利于激发学生数学学习兴趣,提高数学素养,从而使课堂教学更高效.

3 重视变式训练

变式训练是巩固知识、强化解题技能的重要手段.教学中,教师应结合教学实际合理设计变式,从而使一个问题变成一串问题,通过对一串问题的深度思考揭示数学的本质,提高学生的举一反三能力.另外,通过变式训练,可以拓宽学生的视野,帮助学生积累丰富的解题经验,从而使解题变得更高效.

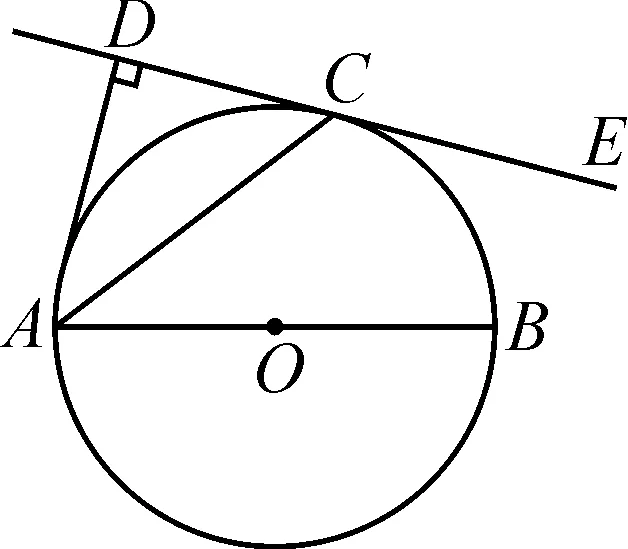
图2

例3如图2,AB为圆O的直径,点C为圆O上一点,AD与过点C的切线垂直于点D,求证：AC平分∠DAB.

问题给出后,教师让学生独立思考,然后展示学生的证明过程.结束本题的证明后,教师给出了如下变式练习：

变式1如图2,AB为圆O的直径,C为圆O上一点,CD是圆O的切线,若AC平分∠DAB,那么AD⊥CD吗?若垂直,请写出证明过程;若不垂直,请说明你的理由.

变式2如图2,AB为圆O的直径,C为圆O上一点,AC平分∠DAB,且AD⊥CD于点D,那么CD与圆O相切吗?为什么?

变式3如图2,点C为圆O上一点,CD是圆O的切线,AC平分∠DAB,且AD⊥CD于点D,那么AB是否为圆O直径呢?

例3是一道典型的几何证明题,难度不大,大部分学生都能顺利解答.为了充分发挥典型例题的教学功能,教师将问题进行改编,以此通过有效的变式训练提高学生应用能力,从而达到触类旁通的效果.

其实,变式训练是教师常用的教学手段.有效的变式训练可以最大限度地启迪学生的思维,让学生一直处于一个轻松的、愉悦的探究氛围中,这样不仅可以激活学生的思维,而且可以提高学生分析和解决问题的能力,切实提高教学质量和学生学习品质.

4 注重思维拓展

良好的数学思维是学好数学的关键,因此培养学生的数学思维能力是初中数学教学的一项基本任务.教学中,教师应结合教学实际设计一些探究性的数学活动,通过深度学习帮助学生厘清问题的来龙去脉,从而达到通一题会一类的效果,切实提高学生解题能力.同时,教学中,教师应重视引导学生经历由特殊到一般的探究过程,让学生感悟数学知识的关联性、规律性,激发学生数学研究的积极性,从而为高效课堂的建构奠基.

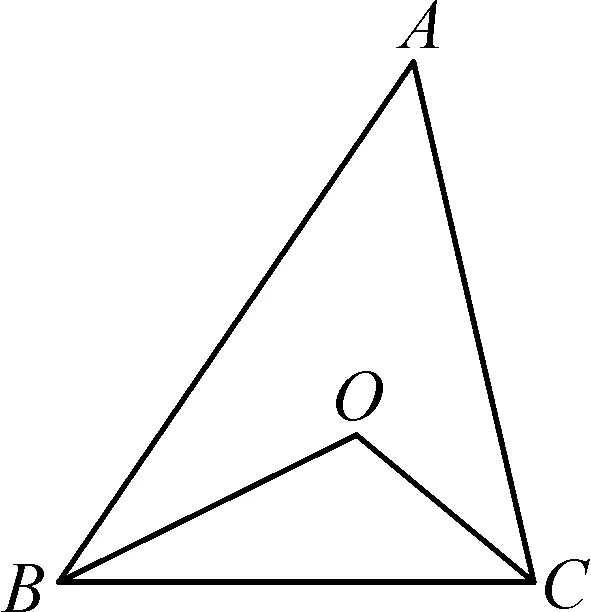
图3

例4如图3,在△ABC中,∠ABC与∠ACB的角平分线交于点O,且∠BOC=126°,求∠A的度数.

该题难度并不大,学生根据角平分线及三角形内角和等相关知识,易得∠A=72°.其实,该题是一个非常典型的练习,在平时练习和考试时经常出现,若想提高学生的解题效率,教师应引导学生充分挖掘其中的规律,以此实现知识的融会贯通.基于此,教师将原题作如下拓展：

拓展1如图3,在△ABC中,∠ABC与∠ACB的角平分线相交于点O,试分析∠BOC与∠A存在的数量关系.

拓展2如图4,在△ABC中,∠ABC与∠ACB的三等分线分别交于点O1,O2,请分别写出∠BO1C和∠BO2C与∠A存在怎样的数量关系?

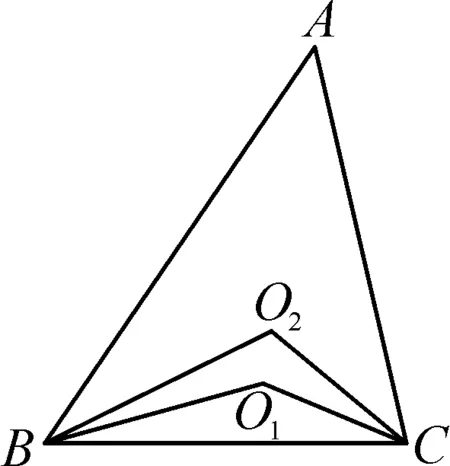
图4

图5

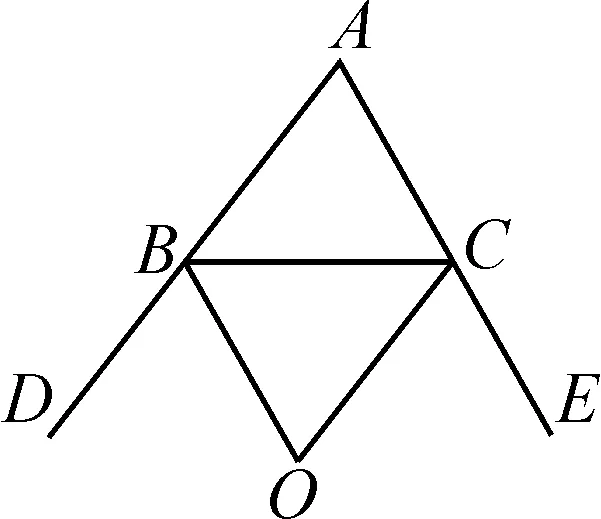
图6

拓展3如图5,在△ABC中,∠ABC与∠ACB的n等分线分别交于点O1,O2,……,On-1,那么∠BOn-1C与∠A存在怎样的数量关系?

拓展4如图6,在△ABC中,BO,CO分别为∠ABC与∠ACD的角平分线,试分析∠BOC与∠A存在的数量关系.

图7

拓展5如图7,在△ABC中,∠ABC的角平分线的延长线与∠ACB的外角平分线相交于点O,试分析∠BOC与∠A存在的数量关系.

图8

拓展6如图8所示,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,探索∠EAD,∠B和∠C之间的数量关系.

这样以学生的已有认知为起点,将一道简单、易于理解的问题通过有效的拓展延伸转化为了一系列问题,丰富了教学内容,开阔了学生的视野.同时,学生经历了由特殊到一般的转化,探究能力也得到了质的提升.

总之,建构高效课堂不应是口号,应该落到实处.教学中,教师要充分发挥其启发者和引导者的作用,通过运用变式训练、思维拓展、反思归纳等活动更好地发展学生,提升教学品质,提高教学效率.