渗透建模思想,强化数学能力*——初中数学教学中学生建模素养发展路径

⦿ 江苏省仪征市月塘中学 雷业红⦿ 江苏省仪征市实验中学东区校 王小琪

“数学发展的根本原动力,它的最初根源,来自客观实际的需要.”数学知识与生活紧密相关,是生活的抽象,并融入生产、生活,为人们的生产、生活提供帮助.数学建模活动的开展,一方面能够让学生的思想更具建模意识,另一方面带给学生解决问题的思路,通过数学建模思想的应用为生活服务.尤其在新课改理念下,渗透建模思想,能让数学教学的开展更具实效,让数学教学成为学生能力发展的动力[1].

1 初中数学建模素养发展的重要性

1.1 培养数学思维

数学教学的开展并非单纯的知识讲解,而是数学思维的培养,让学生因为数学知识的学习而拥有信息分析、独立思考、数学应用等多种能力,能够真正形成数学思维体系.数学建模素养的发展能够让学生逐渐具备数学思维,能够借助数学知识的应用实现能力的更好发展,推动数学知识与生活相结合.

1.2 解决生活问题

数学知识从生活中而来,最终还是要回归到生活之中.只有让数学知识在生活中发挥作用,才能让数学知识的价值得以体现.数学建模素养的发展,能够让学生寻找到解决生活问题的突破口,带给学生思维上的启发,不仅能够让学生的问题解决能力得以发展,而且能够实现数学知识的更好应用,带给学生问题解决的多视角拓展[2].

1.3 激发学习兴趣

从某一个方面来说,数学知识的学习较为枯燥,很多疑难问题往往会阻碍学生对知识的进一步探究.数学建模素养的发展则为学生数学学习兴趣的培养提供助力.很多复杂问题能够通过建模方式变得简便,很多疑难问题能够通过建模方式迎刃而解.这样能增加学习的趣味性,降低数学学习的难度,帮助学生消除学习数学知识的畏惧之心,从而建立学习数学知识信心.

2 初中数学建模素养发展的路径

2.1 建立几何模型

初中阶段学习内容众多,如相似三角形、勾股定理、坐标等,这些知识的学习都离不开几何模型的构建.引导学生构建几何模型,能够让学生的数学建模素养得以提升,形成数形结合思想.

例1一艘海上巡逻舰在海上A处航行,突然接到海上B处指挥中心电话,告知海上有一艘渔船遇险,需要紧急救援.现在得知渔船在指挥中心北偏西60°方向的C处,与巡逻舰相对比,在巡逻舰北偏西30°方向,海上巡逻舰经过定位,发现自己在指挥中心北偏西75°方向,测算之后海上巡逻舰与指挥中心之间的距离为12 n mile,你可以算出海上巡逻舰与待救援渔船之间的距离吗?(结果精确到0.1 n mile.)

此题为航海问题,本质是考查斜三角形的知识.结合题目构建斜三角形,如图1所示.

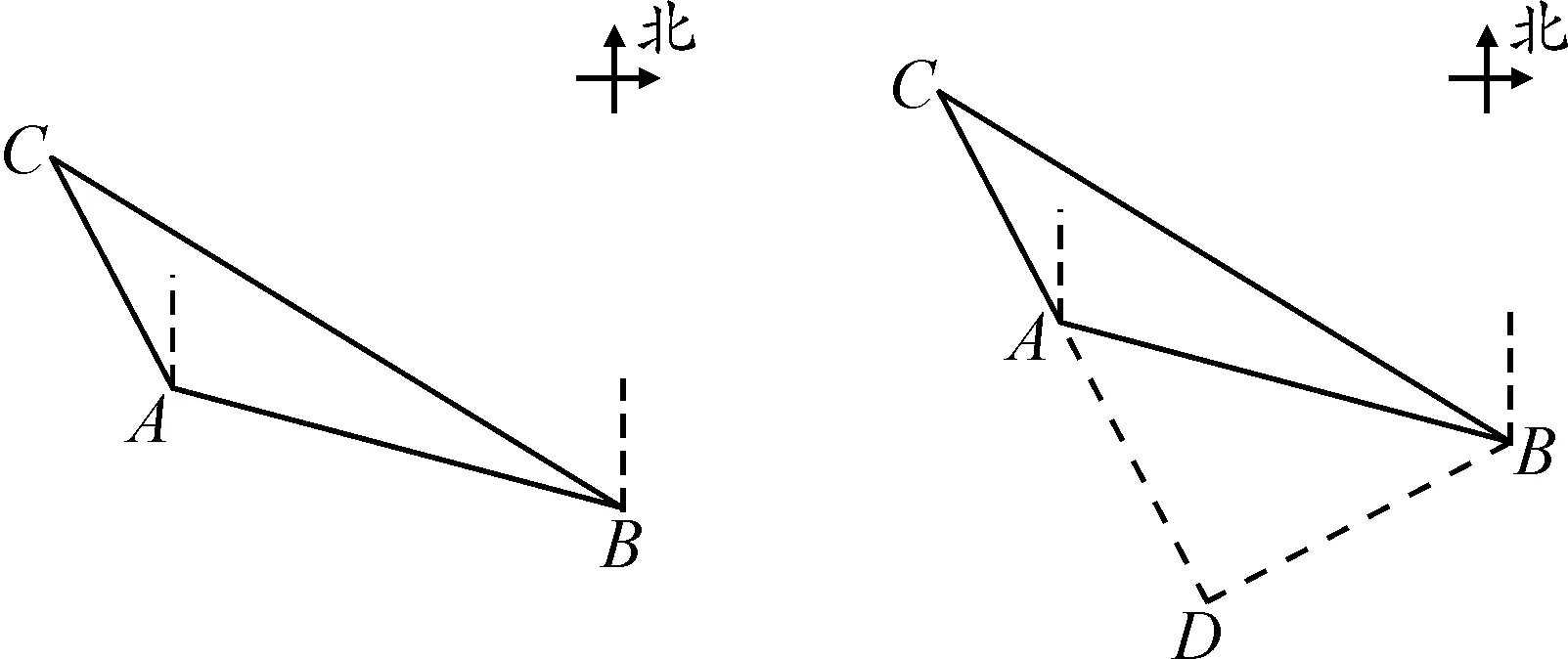
图1 航海问题几何模型

结合构建的几何模型,可以得知本题需要计算A与C之间的距离,则过点B作BD⊥CA,交CA延长线于点D,如图2.

由题意知,∠ACB=60°-30°=30°,∠ABC=75°-60°=15°,所以∠DAB=∠DBA=45°.

故渔船与巡逻船之间相距约6.2 n mile.

通过这样一道典型例题,引导学生形成几何模型构建思维,让学生了解生活中的很多问题都可以借助几何模型解决,同时体会数形结合思想,感受数与形之间的关系.

2.2 建立方程模型

一元一次方程、一元二次方程、不等式是初中阶段的必学内容,这些内容的学习均可以转化为方程模型.通过方程模型的构建,引导学生逐渐形成方程模型构建思维,进而利用方程模型解决相应问题.

例2A超市和B超市准备从市场购买石榴进行销售.已知A超市与B超市购买石榴的预算均为3 000元,且采用不同的方式售卖石榴.A超市依照石榴的大小进行销售,其中大石榴共计400 kg,大石榴按进价的2倍销售,小石榴的售价则高于进价的10%;B超市观察A超市的销售方案之后,所有石榴均按A超市石榴的平均售价销售.两超市石榴售罄之后,A超市盈利2 100元(忽略其他投入成本),那么：(1)石榴进价是多少?(2)哪个超市销售方案盈利更多?

结合题目构建方程模型：

设石榴进价为x元/kg,则方程为

解得x=5.

经检验,得石榴进价为5元/kg.

再结合题目信息,可得B超市盈利为

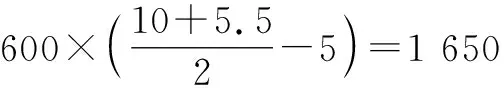
因为A超市盈利2 100元,所以A超市销售方案盈利更多.

方程模型在实际问题的解决中并不少见,但需要注意用方程模型解决实际问题时验证过程不可或缺.

2.3 建立函数模型

初中阶段学生还将学习一次函数、二次函数、反比例函数等知识,针对最值问题则可以通过函数模型的构建予以解决.函数模型的建立,能够深化学生对函数知识的认知,理解函数的意义.在解决问题的过程中渗透函数思想,对学生数学知识体系的构建、建模理念的深化都具有重要影响.

例3如今中学生课余生活丰富,很多学生喜欢骑行,山地车也深受学生欢迎.某车行销售的A品牌山地车,在去年销售总额达到了5万元,为推动A品牌市场占有率,今年A品牌山地车相比较去年每辆售价降价400元,但是销量并没有提升,而是与去年持平,使得销售总额降低了两成.该车行计划新进一批B品牌山地车,两种品牌车辆共计60辆.为控制成本,B品牌山地车进货数量不会超过A品牌山地车数量的2倍,请你结合表1设计进货方案,使这批车盈利最大.

表1 进货和销售价格表 单位：元/辆

设今年新进A品牌山地车为a辆,则B品牌山地车为(60-a)辆,这批车盈利为y元,则有

y=(1 600-1 100)a+(2 000-1 400)(60-a),

y=-100a+36 000.

又60-a≤2a,解得a≥20.

依照一次函数的增减性,当a=20时,ymax=34 000(元).

所以A品牌山地车进货20辆、B品牌山地车进货40辆时,这批车盈利最大.

利用函数的增减性,能够很好地解决生活中所遇到的利润、成本等最值问题.将很多生活中的实际问题转化为函数模型予以解决,能够让学生的函数模型思想逐渐形成并建立.

3 结束语

数学建模教学的开展,知识的立体化是知识渗透之路径,是学生难点突破之方法,是生活问题解决之策略.教师需要更加深度理解数学模型构建理念,了解学生实际情况,从几何模型、方程模型、函数模型等视角入手,教授学生建模方法,推动学生主动探索,引导学生寻找适合自己的数学建模方式.相信随着数学建模思想的渗透,多种教学方法的应用,初中数学教学质量也将不断攀升,学生的数学能力也将不断得到提高.