初中数学“后建构”课堂中问题链的设计研究*——以二次函数最值问题为例

⦿ 无锡市东绛实验学校 陆金花⦿ 无锡市太湖格致中学 陈 锋

1 研究背景

2017年和2018年,江苏省青年教师优秀课(初中数学)比赛别出心裁地分别从“前建构”和“后建构”两个不同视角确定赛题,赛后苏科版初中数学教材主编董林伟先生的总结中,创新性地提出了“后建构课”这一概念,由此引发了学界对“后建构课堂”这种新课堂组织形式的广泛关注.

一般认为“前建构课堂”指的是在建构主义理论指导下的课堂教学,多为新授课;而“后建构课堂”指的是在新认知情境中重组或再构学生已有知识基础,局部深入,以达到重建新的更为完整的认知结构的课堂教学.近年来逐渐兴起的关于初中数学“后建构课堂”的课例研究,给目前乏善可陈的课堂研究注入了新活力.钟鸣关于后建构课堂的章尾复习课展开一定的设计与应用;薛莺基于单元复习设计和多元变式的应用提出关于“后建构课堂”的思考.不难发现,后建构课堂强调教师对知识的重新建构,即打乱原有的顺序,重新建立知识体系,用一条主线将教师想要表达的内容串联起来,在章节复习课和小专题课中作用尤为明显.因此,笔者以两个二次函数最值问题的专题课为例,尝试分析与比较,借此探讨并总结得出后建构课堂应用于初中数学专题课中的一些思考.

2 课例分析

后建构课堂注重知识技能再提升、思想方法再升华、活动经验再积累和核心素养再落实,最重要的是重而不复,其关键之一则是需要厘清内容主线,逐步递进,由一而终.本文中所展示的两个二次函数最值专题课例,切入点有所不同,课堂整体结构和框架也大相径庭,细想之下又觉自然,对最值的理解和内容的定位不同自然可以建构出不同的数学课堂.以下是课例正文.

课例一山重水复疑无路：三提“问”稍显平庸

(1)复习旧知

问题1说一说,根据图1你能获得哪些信息?(顶点坐标、对称轴、增减性……)

函数y=x2-2x-3图1

函数y=-x2+2x+3图2

问题2结合图2,你能解决下列问题吗?

当-1≤x≤0,x______ 时,函数有最大值;x______时,函数有最小值.

当0≤x≤2.5,x______时,函数有最大值;x______时,函数有最小值.

(2)知识应用

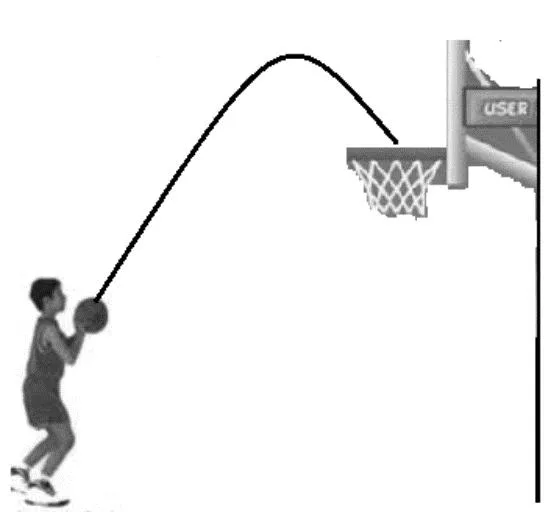
图3

问题3数学来源于生活,生活中处处有数学,尝试解决如下问题.

如图3,通过测量发现,小明投篮时篮球沿抛物线轨迹行进,已知篮框在距离小明4.5 m远,3.05 m高的地方.请同学们算一算篮球能达到的最大高度?

课例二柳暗花明又一村：三个“点”贯通主线

(1)课前提问

问题1抛物线是什么函数的图象?

生：二次函数.

问题2函数图象是由点组成的,点的运动形成图象的高低变化,从而得到了函数的最值.动点问题涉及到的最值模型有哪些呢?

生1：定点与直线上点的连线段中,垂线段最短.

生2：圆上动点与直线上动点所连线段中,线段所在直线过圆心分别得线段的最小值和最大值.

问题3当抛物线上两点都是动点,如何求两动点所连线段的最小值?出示例题.

(2)课堂引入

【一个点】

图4

问题1如图4,请你在抛物线上找一点,使它到x轴的距离最小,最小值是多少?通过类比,可以提出一个有关点到直线距离的最值问题吗?并求出点的坐标.

生1：能否在抛物线上找一点,使它到y轴的距离最小?

生2：能否在抛物线上找一点,使它到直线y=5的距离最小?

【两个点】

问题2如图5-1,连接BC,AC.P为直线BC上方抛物线上一个动点,过点P作PH平行于y轴,交直线BC于点H,求线段PH的最大值.

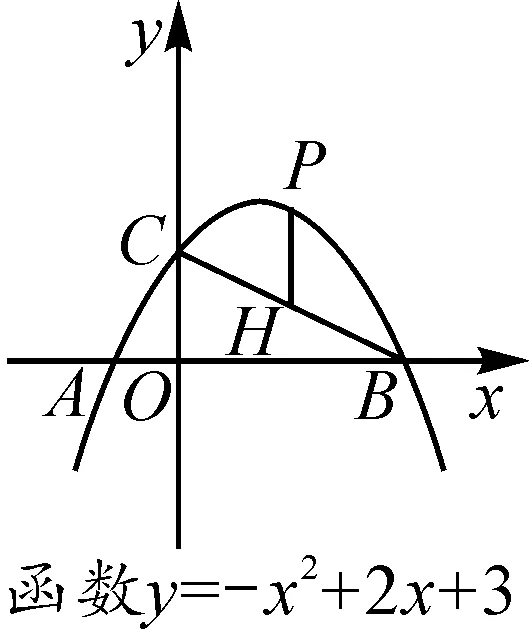
图5-1

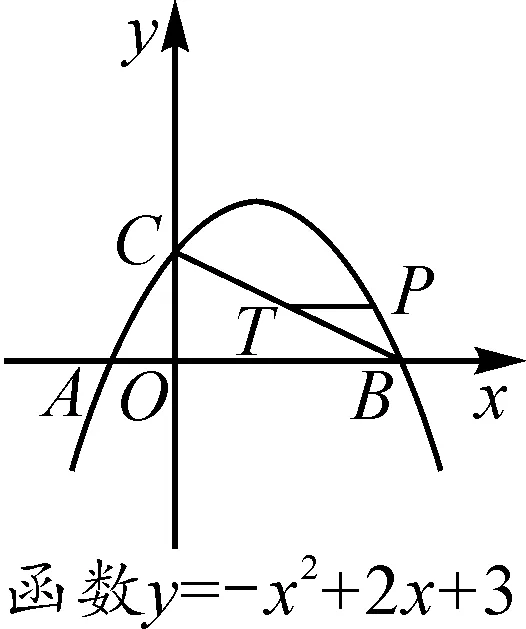
图5-2

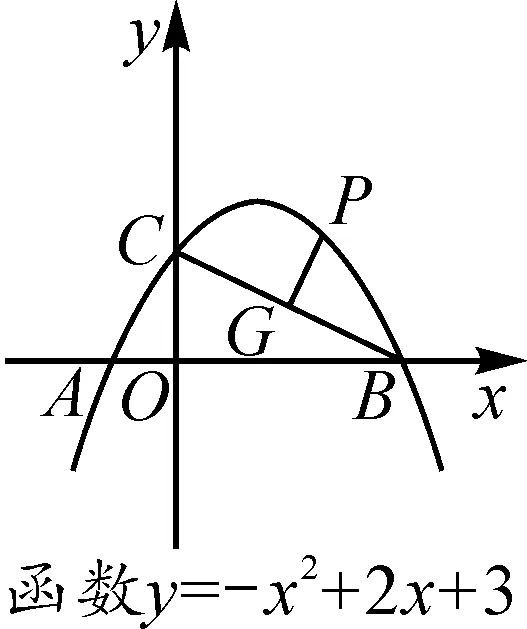
图5-3

类比条件：改变条件PH平行于y轴,其余条件不变,提一个有关线段最大值的问题.

生3：如图5-2,P为直线BC上方抛物线上一个动点,T为线段BC上一点,PT平行于x轴, 求线段PT的最大值.

生4：如图5-3,P为直线BC上方抛物线上一个动点,G为线段BC上一点,PG⊥BC于点G, 求线段PG的最大值.

师：还可以这样变(幻灯片展示),P为直线BC上方抛物线上一个动点,M为线段BC上一点,PM∥AC, 求线段PT的最大值.

(3)拓展延伸

【三个点】

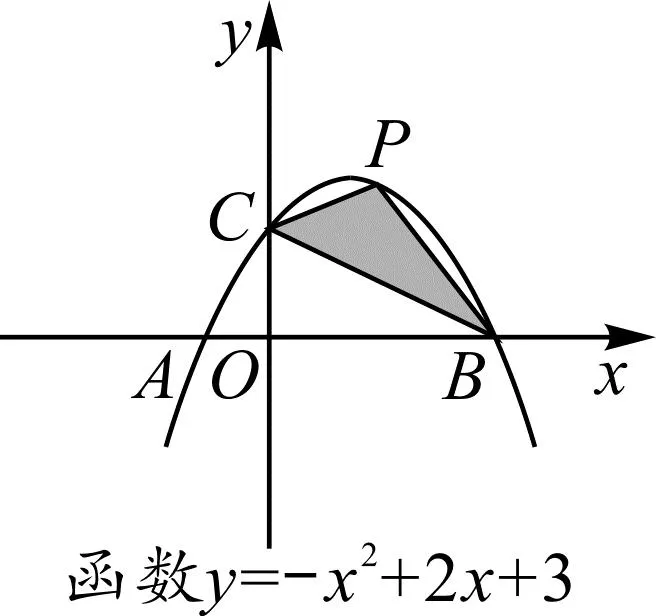
图6

问题3如图6,P为直线BC上方抛物线上一个动点,你能提出一个与三角形面积有关的最值问题吗?

生5：P为直线BC上方抛物线上一个动点, 求△PBC面积的最大值.

教师总结：今天我们研究了抛物线中的动点问题,从一个点,两个点再到三个点,完成了最值问题中点—线—面的转变.

3 “后建构”课堂中问题链设计的思考

中国著名数学家姜伯驹先生曾经说过：数学带给他的最大收益,是学会了长时间思考,而不是匆忙地去处理问题.因此,以一定的逻辑思路,按照整体建构下的数学内容主线,展开一系列深入的问题,激发学生再一次的知识建构,实现前建构与后构建的完美配合,是顺其自然的学习中必不可少的.针对以上两个专题课例,补充几点关于初中数学“后建构”课堂中问题链设计的思考.

3.1 借助问题链精准定位,自然建构认知

函数是中学数学代数部分研究的核心内容之一,也是学生学习数学感觉最困难的内容之一,但是在经历了一次函数和反比例函数的学习后,学生对研究函数的基本过程“概念—性质—应用”已经非常熟悉,所以本节课是基于学生已有的对函数的认知结构和知识结构的一次后建构,借助问题链精准定位,旨在把二次函数最值的相关知识点联系起来,使学生知识实现螺旋式增长,从而提升数学核心素养.课例一中问题链的价值定位于当自变量的取值范围不同时,利用函数图象求最值,通过系列问题链范围实现对最值问题的内化理解和思维提升.课例二中问题链的价值则定位于最值问题在函数图象动点问题中的应用,用一个点、两个点和三个点,勾勒出线段的最值、三角形的面积最值等学生熟悉的最值问题,体现了知识间的联系,同时也让学生深刻地体会了数学思想方法的魅力.在整个教学过程中,系列问题链让学生参与编题且加大了课堂的开放性,让学生能更深入地参与到课堂中.二者虽然定位不同,但都体现了执教者对二次函数最值问题的思考和认识,案例一更适合作为学完整章内容后的专题复习,而案例二更适合学完二次函数的性质后的后建构专题课.

3.2 借助问题链精确引领,揭示教学本质

数学家波利亚指出：“好问题如同蘑菇,他们成堆生长,找到一个以后,你可以在周围找一找,很可能附近就有好几个.”后建构课堂常以问题链的形式将孤立的零散的知识点联系起来,这样既有利于学生的思考,也有利于问题的分析和最终解决.课例二的系列问题链很好地利用了这一形式,针对问题1、问题2,学生再提问,然后所有学生一起解决问题.学生在提问题的时候必然会想到和之前教师给出的问题之间的联系,也必然会以之前的问题为起点,拾级而上,在变中揭示不变的问题本质.不管是教师给出问题还是学生提出问题,最后都会在参与课堂的所有人心中留下深刻的印象.课后再次回想,大脑中留下的不再是单一的题目,而是丰富的、有内涵的动点引发的最值问题.

3.3 借助问题链精细拓展,整体提升素养

后建构课堂不是单一的知识点的重复或再现,也不是刻意加深解题印象,更不是以中考为导向的习题训练课,只求“解对”不求甚“解”,而是在整个课堂中尽量改善固化的教学环节,避免单一的解题方法熄灭学生数学思维的火苗.相较于课例一,课例二的系列问题链的设计不仅表现亮眼,而且在引导学生思考和解决问题上也更胜一筹.如在“三个点”这一环节求三角形面积的最值时,学生非常熟练地说出分割法,即“铅垂直、水平宽”,但仅仅掌握这一方法,对学生来说是远远不够的.解决方法多种多样,各有利弊,没有哪一种方法永远最优.作为教师,要清楚地意识到课堂是提升学生思维的主阵地,如何引导学生提升思维的发散性,对于有限的四十五分钟时间来说至关重要.学生经过长期的锻练,必然能融会贯通,举一反三.

4 结语

课堂是初中数学教学实践的主阵地,如何设计一节融整体性、思维性、趣味性为一体的课堂是每个教师的共同追求,而后建构课堂为我们提供了一种参考方向,可以运用我们的智慧在这种框架结构上串联起一个个问题形成的系列问题链,循序渐进,由浅入深.未来,“后建构课堂”不仅局限于专题课,在试卷讲评课、实践活动课和单元复习课等课型中,也都可以发挥其应有的作用.相信在潜移默化的后建构课堂中,学生能够牢固掌握“四基”,在应用数学知识解决实际问题的过程中切实提高“四能”,最终在学习和应用数学的二次建构中整体完成数学学科核心素养的稳步提升.