联系中重构 打造深度课堂*——以“特殊的平行四边形”的复习教学为例

⦿ 浙江省杭州市富阳区鹿山中学 郑晓华⦿ 浙江省杭州市富阳区郁达夫中学 陈建国

1 基本情况分析

新课教学主要达成的是课时目标,即使是采用整体的方式呈现,也只是结构性的扼要陈述的一些数学对象,当它被单独分析时,会丧失一部分整体的性质.这恰恰体现了复习课的重要地位.复习课显然不是“可有可无”“旧事重提”的课,而是需要教师站在知识的更高位,对学生所学知识进行研究、比较,寻找相互之间的联系和区别,在单元整体观下进行再构造,将原本分散、彼此分割的知识联成一个统一的整体,使学生能在复习中获得系统性的体验.

2 教学过程设计

2.1 知识回溯,唤醒学生的学习起点

课前检测：

(1)矩形具有而一般的平行四边形不具有的特征是( ).

A．有一个角是直角 B．对边相等

C．对角相等 D．对角线互相平分

(2)菱形具有而一般的平行四边形不具有的特征是( ).

A．对角线相等 B．邻边相等

C．对角相等 D．对角线互相平分

(3)菱形的两条对角线长分别为6 cm和8 cm,它的边长是( )cm.

A．10 B．8 C．5 D．6

设计意图：通过前测,唤醒学生对本节课复习的主题内容相关知识点的记忆,便于教师了解学生对特殊的平行四边形知识的掌握情况.

2.2 动手操作,凸显学生的学习体验

已知线段AB的垂直平分线MN,P为MN上一点(在线段AB外),连结AP和BP.

下面是圆圆和芳芳分别在图中作出四边形的步骤.

圆圆：第1步,以过点P且平行于AB的直线为对称轴,将△APB进行翻折,得到△DPC,如图1.

第2步,连接BC,AD,得到四边形ABCD.

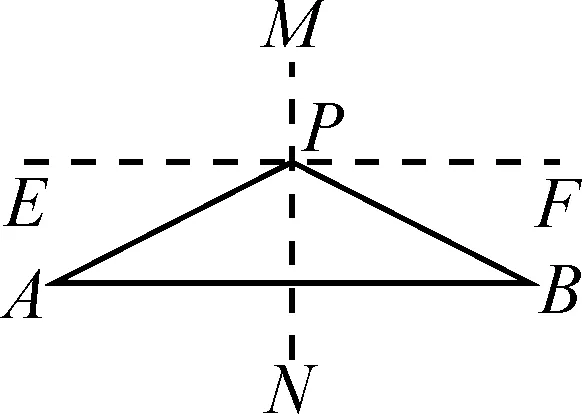
图1

图2

芳芳：如图2,将△APB以AB为对称轴翻折,得到△ABP′,得到四边形AP′BP.

问题1请根据圆圆和芳芳的步骤作出图形.

追问1：作出的四边形是哪一类特殊的四边形?请说明理由.

追问2：能否借助轴对称性来梳理矩形、菱形特有的性质?

师生活动：学生根据要求分别作图,并对所作的图形进行猜想,利用定义和判定进行合理判断,尝试用轴对称性梳理矩形、菱形特有的性质.

设计意图：帮助学生在动手操作中回顾矩形、菱形的定义和判定,体会矩形、菱形(整体)与等腰三角形(局部)具有一致的轴对称性.

2.3 感受优势,激活学生的学习视角

图3

(1)如图3,已知矩形ABCD,BE=CE,则下列结论中正确的是______.

①AE=DE;

②∠BAE=∠CDE;

③BA=BE;

④△ABE≌△DCE.

图4

(2)如图4,菱形ABCD中,E为对角线BD上与B,D不重合的一点,连结EA,EC,你能得到哪些结论?

问题2你是通过什么方法得到这些结论的?

追问1：能否利用它们的轴对称性来解决?

追问2：矩形中点A关于对称轴对称的点是谁?点E呢?AE呢?∠BAE呢?

追问3：若DE=BE,还能得到什么结论?

追问4：根据上述问题1～2,借助轴对称性,能得到哪些等量关系?对后续解决其他问题有什么启示?

生1：通过轴对称,可得相等的线段、相等的角、全等的三角形.凡是对称的图形,都是全等图形.

生2：后续在解决轴对称图形的问题时,可以借助轴对称性,快速判断它们的等量关系.

设计意图：通过问题1～2,帮助学生巩固特殊平行四边形的轴对称性,体会其在解决问题中的优越性,激活学生的思维,从轴对称的视角与方法来看待问题,为后续解决问题打下基础.

2.4 驱动转化,提升学生的学习能力

图5

例题如图5所示,菱形ABCD的面积为20,AB=5,AE⊥CD于点E,连接BD,交AE于点F.连接CF,记△AFD的面积为S1,△BFC的面积为S2,则S1∶S2=______.

问题3由已知条件,你能得到哪些结论?

追问1：如何计算两个三角形的面积比?

追问2：如何求同一直线上的两条线段的比?

思路1：通过对称,聚焦相似三角形,解决问题.

部分学生依据菱形的轴对称性,将△BFC的面积转化为△BFA的面积,进而得到S1∶S△BFA=DF∶BF.利用△BFA∽△DFE,得到DF∶BF=DE∶AB,从而求出S1∶S2.

思路2：通过对称,聚焦两三角形的面积.

部分学生依据菱形的轴对称性,将△BFC的面积转化为△BFA的面积,以△BFA和△AFD的公共边作为底,高分别为AB和DE,从可求出S1∶S2.

思路3：通过对称,聚焦直角三角形,解决问题.

部分学生利用菱形的轴对称性,将△AFD的面积转化为△CFD的面积.由对称性,得AF=CF,∠DAE=∠DCF.依据题干中的条件,可得AE=4,CE=2,由勾股定理或锐角三角函数,可分别求得EF与AF的值.

思路4：通过对称,聚焦角平分线,解决问题.

部分学生利用菱形的对角线平分一组对角,得到SDFE∶S△DFA=FE∶AF=DE∶AD,从而求得结论.

设计意图：通过问题驱动,激发学生的思维,在小组讨论的过程中,找到各种思路的共同点.感受轴对称变换在特殊平行四边形中的运用,学会将四边形问题转化为三角形问题进行解决.同时,回顾解决三角形问题的常用方法,提升学生的推理、运算能力.

问题4如果将例题中的菱形的边长和面积条件都去掉,添加“∠ADC=α”,保留“AE⊥CD于点E,连接BD,交AE于点F.连接CF,记△AFD的面积为S1,△BFC的面积为S2”,是否还能求S1∶S2?

追问1：α确定时,菱形的形状确定吗?刚才的方法是否还适用?

追问2：S1与S2的比值与哪个条件有关?

追问3：如果去掉“AE⊥CD”,设DE∶CE=k,能否求S1∶S2?

设计意图：将问题从特殊推广到一般,感受解决问题方法的不变性,引导学生在具体问题中学会抓住问题的本质,在特殊的平行四边形问题中提升解决三角形问题的能力.

图6

挑战：如图6所示,在正方形ABCD中,点G在BC的延长线上运动,线段AG与对角线BD交于点H,设CG∶BC=k,△ADH和以点C,H,D,G为顶点的四边形的面积分别为S1和S2,求S2∶S1(用含k的代数式表示).

问题5你打算如何求S2∶S1?

追问1：直接求有困难,能否转化?

过点H作HE⊥DC于点E,具体转化过程如图7所示.

图7

2.5 引领梳理,拓展学生的学习深度

(1)等腰三角形与矩形、菱形有什么联系?

(2)借助轴对称的视角研究特殊的四边形,从定性分析,可以得到哪些关系?

(3)利用轴对称性,可以采用什么方法解决特殊的四边形的问题?

轴对称视角下“特殊的平行四边形”复习课的教学内容如图8所示.

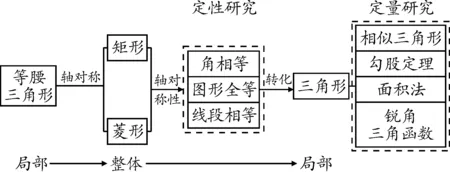
图8

3 教学思考

所谓深度学习,就是指在教师的引领下,学生围绕着具有挑战性的学习主题,全身心积极参与、体验成功、获得发展的有意义的学习过程[1].笔者通过本节课的教学设计与课堂实践,对复习课教学有如下思考与理解.

3.1 知识结构化

数学内容蕴含在数学知识的内部,无法一眼看穿,研究过程中,需要着眼于它与相关内容的联系,在运动变化过程中掌握它.深度学习主张教学内容以内在结构的方式构成学习单元.无论是新课与复习课都主张追寻知识内在的逻辑,通过单元整体的方式展开.这就提醒教师备课时要关注知识的逻辑起点,抓住知识内在的逻辑关系.复习课是对知识进行有序的梳理、联系、拓展,将原本零落分散、彼此分割的知识组成一个个统一的整体.比如,一个数学问题可以有多种表征,代数形式或几何形式,新授课上对二者往往有倾向性,而复习课中就可以将二者有机结合.课堂上,设计恰当的活动,让学生主动、自然地构建知识图谱,获得解决综合性问题的能力.此类复习对学生而言,仍属于一种具有挑战性的学习主题,是一种创造性活动.

3.2 方法再认识

数学方法的认识需要借助解题,但并不是“题海战术”.《礼记·学记》中有云：“道而弗牵,强而弗抑,开而弗抑.”几何教学中的方法较代数而言,缺乏程序性,很难用具体的步骤来描述,在锻炼学生思维的同时,也加大了学习难度.学习解决几何问题的方法,需要学生在过程中不断思考、顿悟、再创造,这就要求教师依据学生的思维路径,有序地呈现学生解决问题的过程、想法,在学生思维受阻时,给予及时的追问,帮助学生找到思路受阻原因,而不是直接强行告知结果.

3.3 经验多迁移

复习课上题不在多,而在于精.选择典型的例题,引导学生掌握研究问题的一般套路.用运动变化的眼光,对所研究的内容进行“特殊化”“一般化”,或者用“类比”等方式,对问题进行再开发,设置便于学生经历“再发现”的过程性问题.不仅在变换形式中挖掘问题的本质,同时,在成功与失败的体验中“学会学习”.学生能够将这种潜移默化的思考习惯、解决问题的一般方法迁移到独立解决新问题中.这样的经验还能帮助学生学会自己发现问题、提出问题、分析问题、解决问题.长此以往,数学对学生而言不再是枯燥的解题,而是像科学家一样在探究问题.

3.4 思想需浸润

数学思想方法需要“言传身教”,需要将其蕴藏在一系列具体的教学内容中.学习应该从什么角度来研究,如何研究,如何拓展研究,课堂上让学生经历实验、猜想、联想、类比、合情推理等分析、解决问题的过程,还原数学家探索、发现事物内在规律的过程.让学生感受前后知识的学习中,研究路径和思想方法的一致性.思考如何将一个新问题转化为已解决的问题.特殊的平行四边形的复习中,可通过中心对称视角、轴对称视角来复习矩形、菱形;通过旋转对称视角来复习正方形.始终不变的是将特殊的四边形问题转化为三角形问题.由此可见,转化、化归等数学思想潜移默化地贯穿课堂始终.

3.5 思维要发展

教之道在于“度”,学之道在于“悟”.教会学生举一反三地学习数学知识,用相同的“套路”解决不同的问题.学生的思维要发展,教师的问题串设计尤为重要.一是情境创设中的问题串设计要由浅入深、循序渐进、相互关联,目的是引发学生的兴趣,帮助学生快速理清已有的知识结构.二是在思维的难点处设计具有启发性的问题串,在相互交流中捋清学生的思维路径,通过问题驱动加以点拨,启发并提高学生的思维.三是在小结环节设计相应的问题串,通过问题串引导学生再次回顾基础知识、基本方法、基本活动经验.给学生充分的思考时间,让他们带着问题思考,有逻辑地探究.

笔者通过本节课的教学设计与展示,以期实现教师对中考复习教学的改进、思考,精准、有效地进行复习教学.当然,由于本人水平有限,教学过程中还有很多可待商榷之处,希望以此起到抛砖引玉的功效,期待更多的数学教育有识之士提出教学建议,共享数学课堂的深度教学.