“三学课堂”,让例题教学活起来*——以切线长定理的解题教学为例

⦿ 江苏省海安市李堡镇丁所初级中学 杜兆俊

著名特级教师李庾南在“自学·议论·引导”教学法的基础上又提出了“学材再建构、学法三结合、学程重生成”的新理念,并着力构建以此为导向的“三学课堂”,其实质是真正以生为本,在充分研判学材、学情、教法、学法、学科关键能力、个体与团体协调持续发展等各类因素的基础上,构建新型生态课堂,既面向全体学生,又适应学生个性发展需要,以期提升学生学力,培养“全面发展的人”[1],实现学科教学改革,为学生终生学习奠定基础.笔者以切线长定理的解题教学为例,与大家分享和研讨.

1 教学案例

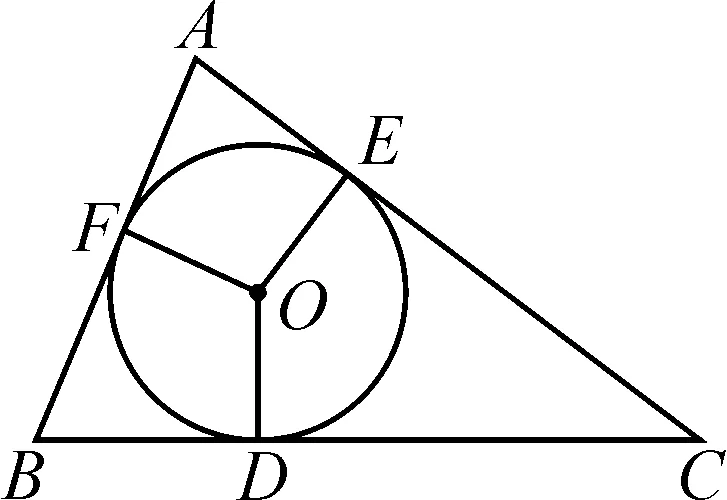
图1

例题(人教版义务教育课程标准实验教科书数学九年级上册第100页例2)如图1,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9,BC=14,CA=13.求AF,BD,CE的长.

1.1 一题多解,大胆尝试,提升思维广度

引导学生分析例题中的已知条件,尝试用不同的方法解题,逐步培养从不同角度切入并思考问题的习惯,加深对所学知识的理解,训练对所学方法的运用.学生先个人研究,再进行小组合作探究,最后全班交流讨论,汇报解法.主要有以下两种解法.

方法1：列一元一次方程求解(课本解法).

解法1：设AF=x,则AE=AF=x,CD=CE=AC-AE=13-x,BD=BF=AB-AF=9-x.

由BD+CD=BC,可得(9-x)+(13-x)=14,解得x=4.因此AF=4,BD=5,CE=9.

方法2：列三元一次方程组求解.

故AF=4,BD=5,CE=9.

1.2 一题多变,回归课本,提升思维高度

在解题教学中,结合学生的实际情况,关注例题的“生长点”与“延伸点”,对例题进行变式和拓展,同时还要考虑到大部分学生能听懂,力争一课一得,使知识活学、活用,使方法熟练、精通,使技巧丰富、自如.

变式1△ABC的边长AB=9,BC=14,CA=13,求△ABC的面积.

图2

生1：如图2,作BC边上的高AD.由勾股定理,得AB2-BD2=AD2=AC2-CD2,即92-BD2=132-CD2.

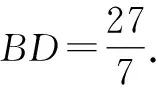
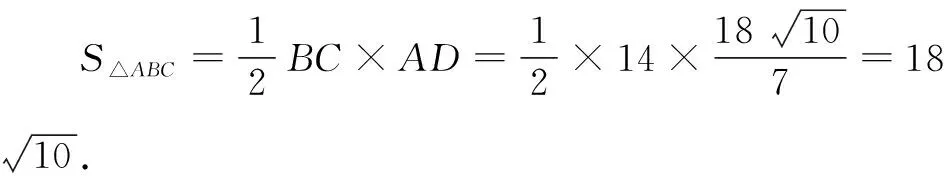
变式2如图1,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9,BC=14,CA=13,求内切圆⊙O的半径r.

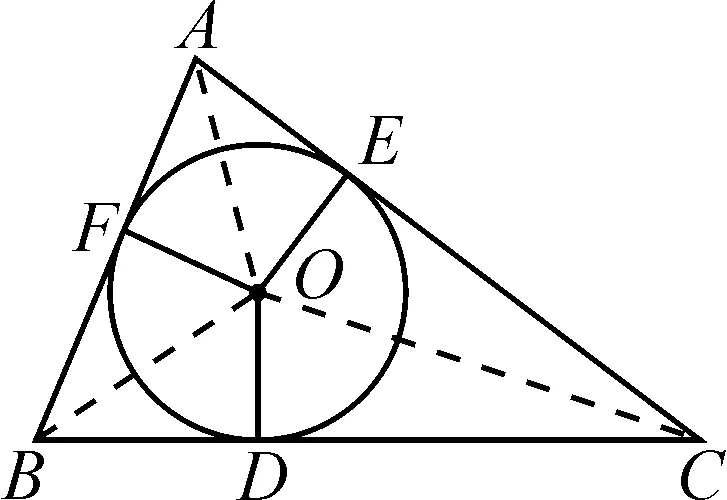
图3

生2：如图3,连接AO,BO,CO,则有

变式3(人教版义务教育课程标准实验教科书数学九年级上册第100页练习2)△ABC的内切圆半径为r,△ABC的周长为l,求△ABC的面积.(提示：设内心为O,连接OA,OB,OC.)

生3：设AB=c,BC=a,AC=b,则l=a+b+c,连接AO,BO,CO,则由变式2可知

变式4已知△ABC的面积为S,△ABC的周长为l(或三边长为a,b,c),试用S,l(或三边长为a,b,c)表示△ABC的内切圆半径r.

图4

变式5(人教版义务教育课程标准实验教科书数学九年级上册第103页第14题)如图4,Rt△ABC中,∠C=90°,AB,BC,CA的长分别为c,a,b.求△ABC的内切圆的半径r.

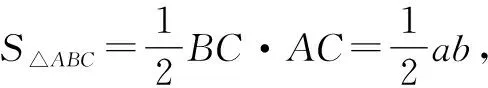
1.4.3 T细胞亚群水平 观察两组患者术前及术后6、12、24、48 h血浆中CD3+T细胞、CD4+T细胞、CD8+T细胞、CD4+/CD8+水平。采用CytoFLEX型流式细胞仪[贝克曼库尔特商贸（中国）有限公司]检测CD3+T细胞、CD4+T细胞、CD8+T细胞、CD4+/CD8+水平（试剂盒由晶美生物工程有限公司提供）。

1.3 一题多悟,生成新法,提升思维深度

数学是一个有机的整体,要用整体的观点把新学的知识与已学的概念、定理、公式等连成线、结成网,从而沟通不同知识之间的内在联系,有利于提高学生分析和解决问题的能力.

图5

生6：如图5所示,设Rt△ABC的内切圆与三边相切于点D,E,F,连接OD,OE,OF.因为⊙O为Rt△ABC的内切圆,所以OD⊥AC,OE⊥BC,OF⊥AB,OD=OE=r,AD=AF,BE=BF,CE=CD.所以四边形ODCE为正方形,则有CE=CD=r.设AD=AF=x,BE=BF=y,则有

①

②

③

①+③-②,得

(x+r)+(y+r)-(x+y)=a+b-c.

三角形的内切圆半径长度是确定的,两种方法求出的结果应该相同,但为什么表达形式却“不一样”呢?学生一脸茫然,感到很意外：在不同方法下计算的结果,怎么会出现“不一样”的两个答案?心理产生了矛盾,思维发生了冲突.此时,教师没有直接引导大家运用勾股定理来验证两种结果是否一样,而是话锋一转：这两种不同的方法计算出的结果应该相等,若令它们相等会出现什么结果呢?请大家尝试一下.

顿时,整个教室像炸开锅似的热闹非凡,学生情绪高涨,展开了热烈讨论.

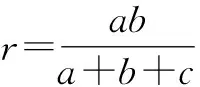
学生们惊呼：勾股定理!我们竟然发现了一种证明勾股定理的方法,真是意外收获!

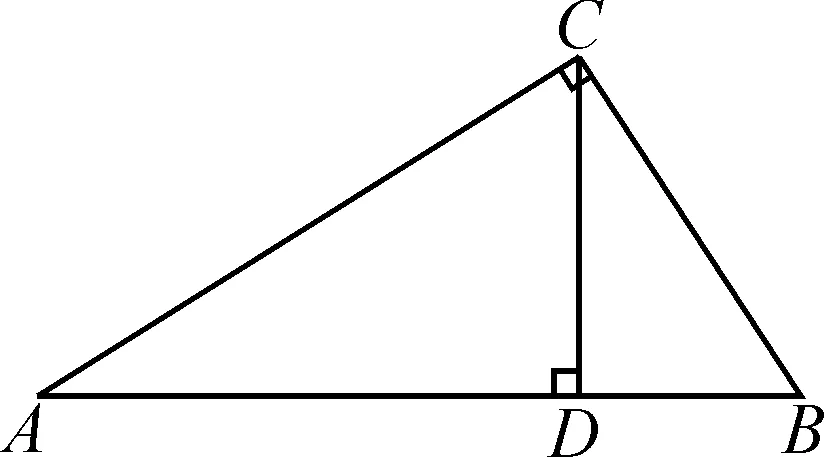
图6

后来,生8在完成作业人教版义务教育课程标准实验教科书数学九年级下册第36页练习2“如图6,Rt△ABC中,CD是斜边AB上的高.求证：(1)△ACD∽△ABC;(2)△CBD∽△ABC”后,又发现了一种证明勾股定理的方法：

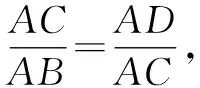
AC2=AD·AB.

④

BC2=BD·AB.

⑤

④+⑤,得AC2+BC2=AD·AB+BD·AB=(AD+BD)·AB=AB2.

2 教学反思

2.1 在设置变式练习中“学材再建构”

只有进行科学高效的“学材再建构”,才能确保精彩的生成.数学教材中的例题、习题凝聚了编者的心血,具有典型性、生成性,为中考命题提供了宽广的空间.在近几年的中考中,很多试题“源于课本而又高于课本”,这无疑暗示了一种教学导向,那就是教师要深入研究课本,即根据教材和学生实际情况,通过精选、改编教材中的例习题,合理整合教材,进行“学材再建构”,帮助学生系统地掌握知识,让学生初步经历数学发现、数学探究、数学创造的过程.本课在课本例题解法研究的基础上,对例题进行适当改编,由例题“发枝散叶”出五个变式问题(其中两个是课本原题),从一般到特殊,形成问题串,层层深入,步步提升.引导学生先探究普通三角形的内切圆半径公式,再探究直角三角形的内切圆半径公式,然后由其两种不同的表达形式的“矛盾”出发,证明了“勾股定理”,构建了数学的“知识树”.这样既能使学生深入理解概念、定理,掌握解题技巧,又能抑制“题海”战术,达到做一题、学一法、会一类、通一片的目的.

2.2 在营造有效互动中“学法三结合”

李庾南老师的“自学·议论·引导”教学法的核心理念是：以学生为主体,在师生合作中学会学习,获得自主发展[3].本节课通过对一组变式问题的求解,激起学生的认知冲突,引发学生的议论.通过“独立思考”“小组合作学习”和“全班学习”三种学习方式,每个学生都能进入深度思考,进行观察、分析、类比、归纳、猜想、推理等活动,说出自己对问题的不同看法,并加以验证.在这一期间,学生可以用不同的方式——个人学习、小组学习、全班学习,进行讨论和争辩,直至最终达成解决问题的共识.个人学习有利于培养学生独立思考的习惯,而小组学习、全班学习有利于培养学生合作精神,三者有机结合,可以更好地将学习推向深入,变“要我学”为“我要学”,学生真正成了学习的主体、探究的主体以及自我发展的主体.

2.3 在捕捉思维火花中“学程重生成”

学生是一群充满活力和个性的生命体,在教学过程中会出现怎样的情况,教师无法全部估计到.所以教师在教学过程中要做到从学生出发,给学生“生成”的空间,让学生的思维“暴露”出来,敏锐捕捉在生生互动、师生互动的交流合作中不期而至的生长点,不失时机地利用好生成性资源.尤其是解题教学中,注重方法提炼,从而真正实现“学程重生成”.本课中学生用刚刚“发现”的规律,生成了证明勾股定理的方法,后来还在证明相似三角形的过程中,又发现了一种证明勾股定理的方法,这正是学生可持续学习能力的体现.从上述案例的分析可以看出,具有生成性的教学才是有效的课堂教学.我们的课堂需要教师善于捕捉和及时把握最佳教学时机,处理得当,点拨到位,学生的创新思维才会得到最大限度的激活,教师的巧妙处理就能起到“四两拨千斤”的绝佳效果.教师的作用不再是去填满“仓库”,而是要点燃火炬,捕捉学生思维的火花;学生学习的灵感在积极发言中、相互辩论中突然闪现,最终达到“养成认真勤奋、独立思考、合作交流、反思质疑的学习习惯”[4].