HPM视角下“正弦定理”的教学*

夏 宇

安徽省宿城第一中学

HPM是数学史与数学教育之间关系的简称,数学史融入数学教学是当下HPM研究的一个重要领域.在高中数学中,正弦定理是求解三角形的重要工具.在“正弦定理”的教学中,教师应该尝试多种不同的教学模式.翻开数学史料,笔者发现古人已经探索出多种不同的正弦定理的证明方法,有不少漂亮的证法有必要介绍给学生,让学生感受古人的智慧.基于此,本文中在HPM视角下,开发不同于以往的“正弦定理”的教学设计.

1 历史的回顾

三角学研究历史悠久,中国古代数学家商高和古希腊数学家毕达哥拉斯都证明了直角三角形中的勾股定理.对于反映任意三角形中边角关系的正弦定理,虽然在历史上发展较为缓慢,但也有不少证法.阿拉伯数学家和天文学家纳绥尔丁[1]最早用同径法证明了正弦定理;16世纪中叶,法国数学家韦达在《数学法则》中借助外接圆证明了正弦定理;17世纪,英国数学家哈里斯利用直角三角形法证明了正弦定理;19世纪,尼克逊用辅助直径法证明了正弦定理;上世纪50年代,逐渐出现了解析几何的方法.随着数学家们对正弦定理坚持不懈的研究,其证明方法也越来越多姿多彩.教师带领学生跟随古人的脚步,探索方法,体会思想,提升素养.

2 教学设计与实施片段

2.1 引入

师:在初中阶段,我们学习了勾股定理和锐角三角比,能够在直角三角形中进行边角的计算.我们也知道,在任意三角形中,大边对大角,小边对小角,那如何准确表达任意三角形的边角关系呢?这就是今天要给同学们介绍的正弦定理.

2.2 知识生成

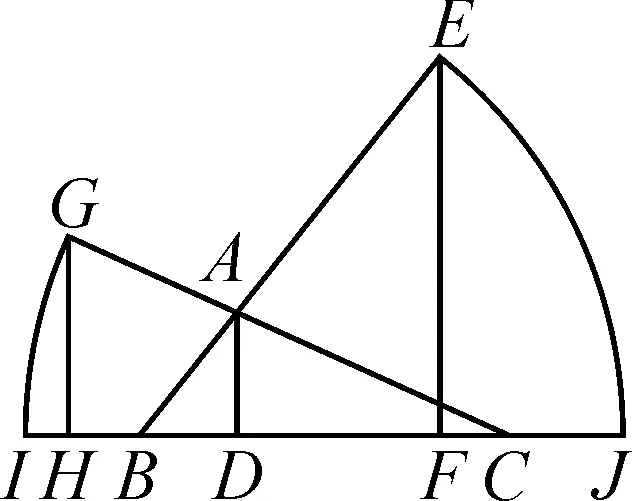
图1

生:正弦定理结构对称,内容简洁.纳绥尔丁的作图比较巧妙,但证法有点繁琐,不易想到,可望而不可即.

师:巧妙的证明说明古人对问题进行了深入研究和持续的思考,值得我们学习.

2.3 方法探究

师:16世纪中叶,法国数学家韦达在《数学法则》中借助外接圆证明了正弦定理.如图2,△ABC外接圆圆心为O,半径为R,作OD⊥BC于点D,作OE⊥AC于点E,作OF⊥AB于点F.你能根据图形试着证明正弦定理吗?

图2

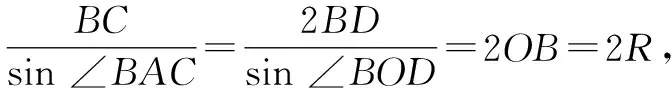
师:很好!

生:这不仅证明了正弦定理,还可以看出定理中的比值是有几何意义的,这个比值就是△ABC外接圆的直径.

师:是的,这种证法逻辑清晰,简洁明了.我们再次体会了古人的睿智.

师:17世纪,英国数学家哈里斯利用直角三角形法证明了正弦定理.如图3,在△ABC中,AD⊥BC于点D.请同学们思考,哈里斯是如何证明正弦定理的?

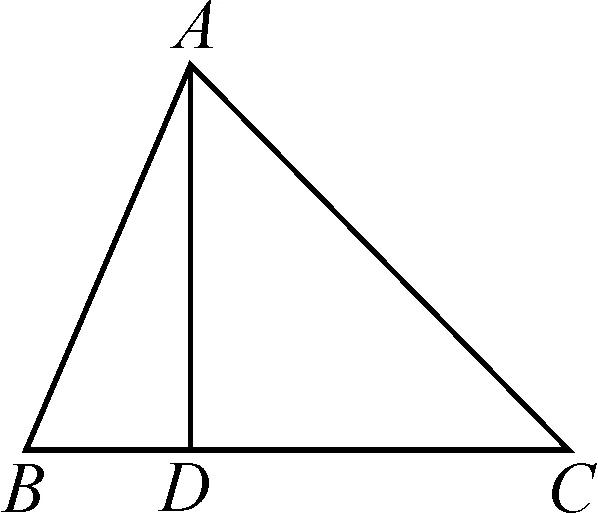
图3

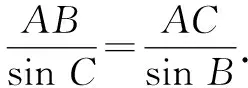
生:这种证法也很简洁啊!

师:19世纪,尼克逊用辅助直径法证明了正弦定理.如图4,在△ABC中,AD⊥BC于点D,作△ABC外接圆O,直径BE=2R,连接EA,EC.请同学们结合图形思考,尼克逊是怎样证明正弦定理的?

图4

师:很好,同学们能将前面的证法进行迁移.

师:上世纪50年代,逐渐出现了解析几何的方法.在△ABC中,建立如图5所示的两种平面直角坐标系,你能分别写出点C的坐标吗?又如何证明正弦定理呢?

① ②

师:很好!这样我们大致把古人对正弦定理的证法梳理了一番,大家有什么体会呢?

生:可以看到,随着数学的发展,证明思路越来越多,证明方法越来越简洁.每一种方法都值得我们好好领悟.

生:是的,我们不能低估古人的智慧,要学习他们研究问题时追求严谨的科学精神以及坚持不懈的意志品质.

师:同学们说得非常好!其实数学家们还有其他一些证明正弦定理的方法,同学们可以课下再去查阅资料.

3 教学感悟

首先,本节课笔者对数学史料的应用方式主要是复制式和重构式[2].纳绥尔丁的证明方法比较麻烦,所以通过复制式直接介绍给学生,重在体会理解;后面几种方法较为容易,所以通过重构式带领学生一起探究.通过实践发现,在HPM视角下进行正弦定理的教学,学生兴趣高昂,思考积极,整堂课鲜活、有趣、精彩、有生命力,效果很好.

其次,在教学中渗透数学家的故事,介绍数学知识的演进,可以让学生体会知识之和谐,方法之多变,探究之美妙.

知识之和谐:在教学中,注意引导学生去体会正弦定理的简洁性、对称性;在用各种方法证明时,体会思路的自然生成.

方法之多变:通过多种方法的探究,开阔了学生的视野,提高了他们一题多解的能力,提醒数学的学习需要解放思想,创新进取.

探究之美妙:教师作为引导者,引领学生去思考,去解决问题,学生在一次又一次的艰辛思考中,体会到数学探究的美妙之处.

最后,笔者认为,HPM视角下的数学教学既可以提升学生核心素养,也可以发挥其德育价值.例如,本节课中,以问题驱动学生去寻找知识本源,提升逻辑推理素养;以图形为辅助,提升直观想象素养.本节课的教学过程也是正弦定理的历史发展过程,学生在探究中受到数学文化的浸润,这种文化的力量会持续地影响学生的思维习惯.同时,学生也会学习到数学家们求真、求善、求美的精神和坚毅的品质.