一题多解和一题多变:一道有关抛物线焦半径问题的探究*

吴玉章 苗庆硕

江苏省新沂市第一中学

抛物线的焦半径问题是抛物线综合问题中的一类特殊类型,其可以联系起抛物线的定义(问题的本质)、几何性质(“数”的属性)与几何特征(“形”的特征)、焦半径公式(三角形式)等,“串联”起平面解析几何、平面几何、函数与方程、三角函数等众多相关知识,为问题的切入与解决提供较多的思维视角,给问题的解决提供更多的方案与技巧方法,是有效发散数学思维,考查学生“四基”、数学能力以及数学思想方法等方面比较有效的一个重要载体,备受各方关注.

1 问题呈现

问题已知抛物线y2=8x的焦点为F,准线与x轴的交点为C,过点C的直线l与抛物线交于A,B两点,若∠AFB=∠CFB,则|AF|=______.

此题以抛物线为问题场景,通过设置过准线与x轴交点的直线l与抛物线交于两点,利用两个角相等来创设定交点问题,进而求解相应焦半径的长度.

涉及抛物线的焦半径问题,可以从解析几何的实质入手,利用解析几何思维来合理进行数学运算与分析处理;也可以从平面几何的图形入手,利用平面几何思维进行逻辑推理与分析处理;还可以从焦半径的公式入手,利用三角函数思维来合理数学运算、逻辑推理与综合应用等.不同思维视角的切入,都给问题的解决提供了切实可行的技巧与方法,实现问题的巧妙解决.

2 问题破解

2.1 解析几何思维

解法1：设线法.

依题意可得p=4,则F(2,0),C(-2,0).

根据已知可得直线l的斜率存在且不为0,利用图形的对称性,不失一般性,设点A,B位于x轴的上方,如图1所示.

图1

设直线l的方程为x=my-2,其中m>0.设A(x1,y1),B(x2,y2),y1>y2>0.

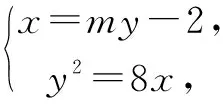
y2-8my+16=0.

利用韦达定理,可得y1+y2=8m,y1y2=16,则

由抛物线的定义,可得

解后反思：设线法是借助解析几何思维处理问题的一种“通性通法”,成为解决直线与圆锥曲线位置关系问题时首选的一种基本方法.

2.2 平面几何思维

解法2：几何法.

依题意可得,p=4.

根据已知可得直线l的斜率存在且不为0,利用图形的对称性,不失一般性,设点A,B位于x轴的上方,如图2所示.

图2

过点A,B作抛物线准线的垂线,垂足分别为D,E,延长EB交AF于点G.

由于EG∥CF,因此∠GBF=∠CFB,又∠AFB=∠CFB,所以∠AFB=∠GBF,可得|BG|=|FG|.

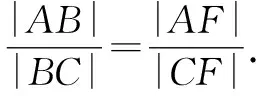
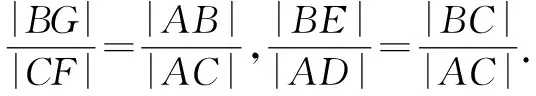
所以有|BG|·|AC|=|BE|·|AC|,可得|BG|=|BE|,又结合抛物线的定义有|BE|=|BF|,故|BG|=|FG|=|BF|,即△BFG是正三角形,从而∠BFG=60°,可得∠AFx=60°.

解后反思：平面解析几何侧重“数”与“形”的结合与转化,借助代数思维中的数学运算来处理几何图形中的逻辑推理问题等,实现问题的突破与应用.

2.3 三角函数思维

解法3：性质法.

依题意可得,p=4.

根据已知可得直线l的斜率存在且不为0,利用图形的对称性,不失一般性,设点A,B位于x轴的上方,如图3所示,过点A,B作抛物线的准线的垂线,垂足分别为D,E.

图3

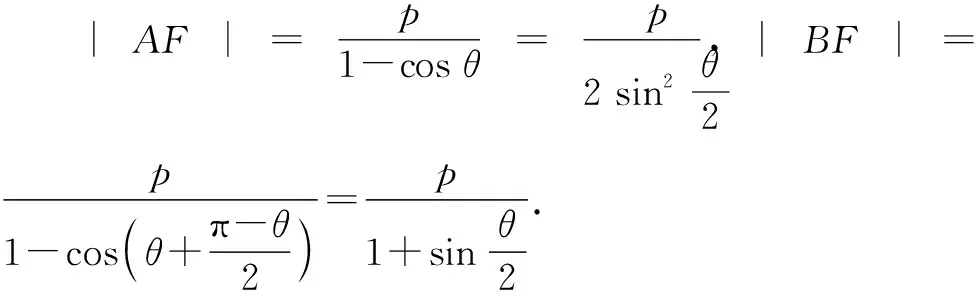
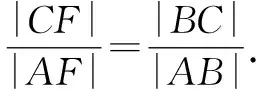
3 变式拓展

3.1 同源变式

变式1己知抛物线y2=8x的焦点为F,准线与x轴的交点为C,过点C的直线l与抛物线交于A,B两点,若∠AFB=∠CFB,则|BF|=______.

在此基础上,可以对问题进行一般化的归纳与总结.

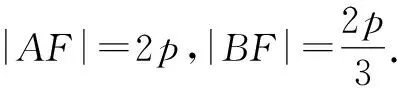
变式2己知抛物线y2=8x的焦点为F,准线与x轴交于点C,过点C的直线l与抛物线交于A,B两点,若∠AFB=∠CFB,则|AB|=______.

3.2 同阶变式

变式3已知抛物线y2=8x的焦点为F,准线与x轴交于点C,过点C的直线l与抛物线交于A,B两点,若∠AFB=∠CFB,则直线AF的斜率为______.

4 教学启示

此类涉及抛物线的焦半径问题,往往是多知识点交汇与融合的产物,这样的创设契合高考数学命题精神,而多知识点交汇也为问题的切入提供了更多的思维视角,给各层面的学生提供了更多的机会,从而更加有效地体现数学试题的选拔性与区分性.

在数学学习中,针对此类涉及圆锥曲线的焦半径问题,要深刻体会并加以系统学习,把握问题的实质与内涵,构建知识体系,理解技巧方法,形成解题习惯,培养数学品质.