四点共面,链接教材,变式拓展
——以一道高考题为例

2024-01-19 10:25陶贤

中学数学 2024年1期

陶贤

江苏省张家港市沙洲中学

空间中的四点共面的判断与证明是空间向量与立体几何部分的一个基本知识点,也是一大难点,历年高考数学试题中较少涉及,没有引起大家的高度重视.而在2020年高考数学全国卷Ⅲ的文科和理科试题中,都出现了空间四点共面的证明问题,也充分说明了该部分知识的基础性与重要性.借助空间中四点共面的判断与证明,很好地考查考生的数形结合思想、空间想象能力与推理论证能力,以及直观想象、逻辑推理等数学核心素养.

1 真题呈现

高考真题(2020年高考数学全国卷Ⅲ理科第19题)如图1,在长方体ABCD-A1B1C1D1中,点E,F分别在棱DD1,BB1上,且2DE=ED1,BF=2FB1.

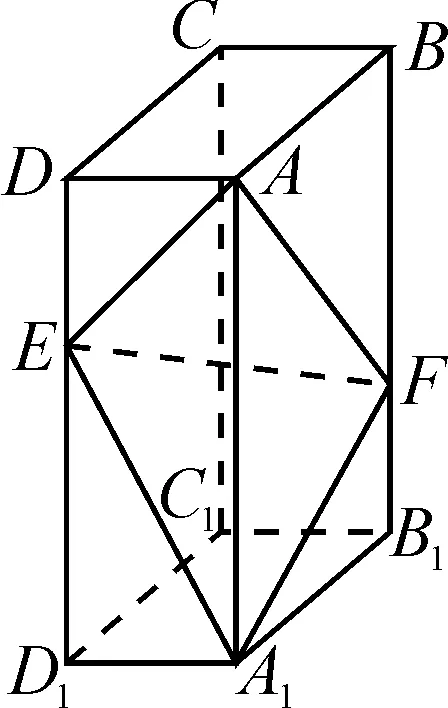
图1

(1)证明:点C1在平面AEF内.

(2)若AB=2,AD=1,AA1=3,求二面角A-EF-A1的正弦值.

此题以长方体为问题背景,通过相应线段的长度关系,证明点在平面内(其实就是证明四点共面)以及求解二面角的平面角的正弦值,改变以往传统的证明直线与平面之间的平行或垂直关系,令人耳目一新.

2 问题破解

(Ⅰ)第(1)问的证法如下:

证法1：几何法.

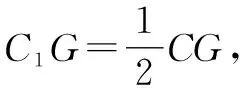
图2

在长方体ABCD-A1B1C1D1中,AD∥BC且AD=BC,BB1∥CC1且BB1=CC1.

又BC∥AD且BC=AD,所以AD∥GF且AD=GF,即四边形AFDG是平行四边形,则AF∥DG且AF=DG.

同理可证,四边形DEC1G为平行四边形,则C1E∥DG且C1E=DG.

所以C1E∥AF且C1E=AF,则四边形AEC1F为平行四边形.因此,点C1在平面AEF内.

证法2：基底法1——共面向量定理.

在长方体ABCD-A1B1C1D1中,BB1∥CC1∥DD1且BB1=CC1=DD1,结合2DE=ED1,BF=2FB1,可得ED1=BF.

证法3：基底法2——共面向量定理的推论.

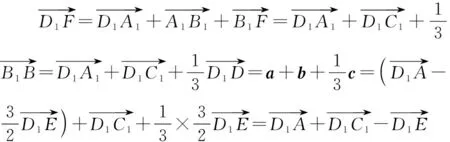
证法4：坐标法.

图3

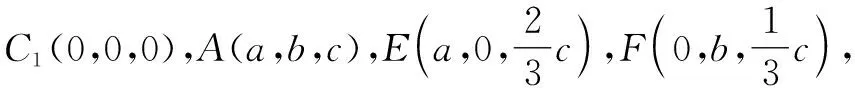
点评：证明空间中的四点共面问题,常见的证明方法就是以上三大类——(1)利用空间几何图形的特征,借助几何法的推理与论证,通过空间问题平面化来证明;(2)利用共面向量定理或推论,借助空间向量的基底法,通过向量的线性运算与转化来证明;(3)利用空间直角坐标系的建立,借助坐标法的运算,通过向量的平行判断与转化来证明等.特别地,对于共面向量定理及其推论,是立体几何中的一个重要的定理,可以用来处理一些与之相关的问题,往往可以使问题处理得更加简捷、巧妙.

(Ⅱ)第(2)问的解法如下:

设平面AEF的法向量为m=(x1,y1,z1).

设平面A1EF的法向量为n=(x2,y2,z2).

点评：坐标法是求解二面角的平面角的三角函数值问题中一个比较常见的方法,借助空间直角坐标系的建立,以及对应的点、向量的坐标的表示,结合相应两半平面的法向量的设置与确定,结合向量的数量积公式的转化与应用来确定相应的二面角的平面角问题.坐标法实现了用代数方法处理立体几何问题中的四点共面、线面位置关系、空间角、距离等几何推理与求解问题.

3 链接教材

以上基于向量的四点共面的判断,其对应的共面向量定理及其推论是数学教材中的一个基本知识点,来源于教材,又服务于证明,可以很好地证明或求解与四点共面有关的数学问题.

普通高中课程标准实验教科书《数学·选修2-1》(人教A版)第87页:

结论1：共面向量定理.

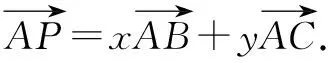
普通高中课程标准实验教科书《数学·选修2-1》(人教A版)第88页“思考”:

结论2：共面向量定理的推论.

共面向量定理是共线向量定理在空间中的推广与拓展,共线向量定理用来证明三点共线,共面向量定理用来证明四点共面.

4 变式拓展

高考真题(2020年高考数学全国卷Ⅲ文科第19题)如图4,在长方体ABCD-A1B1C1D1中,点E,F分别在棱DD1,BB1上,且2DE=ED1,BF=2FB1.证明:

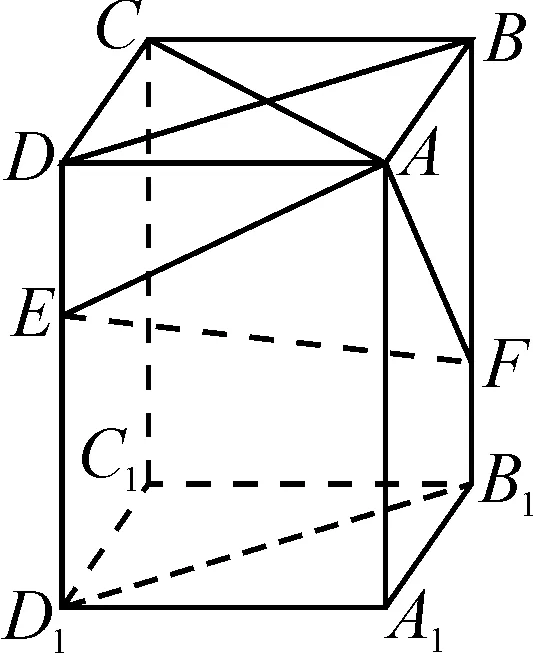
图4

(1)当AB=BC时,EF⊥AC;

(2)点C1在平面AEF内.

证明：(1)连接BD,B1D1.

因为AB=BC,所以四边形ABCD为正方形,故AC⊥BD.

又因为BB1⊥平面ABCD,于是BB1⊥AC,而BD,BB1⊂平面BB1D1D,所以AC⊥平面BB1D1D.

因为EF⊂BB1D1D,所以EF⊥AC.

(2)可以参照上述理科真题第(1)问的证明方法.

5 解后反思