直觉引领 运算探究 模型回归——以2023年全国乙卷(理科)第20题为例

孙爱文 张 凡

江苏省沭阳高级中学

1 试题呈现

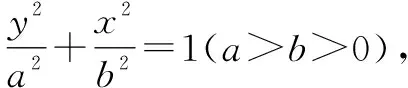
(1)求曲线C的方程;

(2)过点(-2,3)的直线交曲线C于P,Q两点,直线AP,AQ与y轴交于M,N两点,求证:MN的中点为定点.

2 试题分析

本题第(1)问为常规的求曲线方程问题.第(2)问考查定点问题,这是近几年最为风靡的齐次化联立模型,背景是极点、极线,考查了解析几何的基本思想和基本方法,对学生运算能力的要求很高,体现了逻辑推理、数学建模、数学运算等核心素养.现给出第(2)问的解题思维导图,如图1所示.

图1

3 试题详解

思路1：从必要条件出发,先猜后证.

解法1：设P(x1,y1),Q(x2,y2),M(0,y3),N(0,y4),T(-2,3).

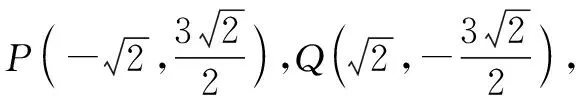
图2

或者极限分析,PQ无限趋近于一点时,PQ直线方程为y=3,此时M(0,3),N(0,3)故MN的中点为定点为(0,3).再作如下证明:

联立直线AM与椭圆方程,得(m2+6m+18)x2+4(3+m)2x+4m2+24m=0.

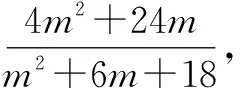
解法2：设线法+韦达定理.

设lPQ:y=k(x+2)+3,P(x1,y1),Q(x2,y2),M(0,y3),N(0,y4),则

对于lAP和lAQ,令x=0,可得

①

故MN的中点为定点(0,3).

解法2的优化:整体代换.

设lPQ:y=k(x+2)+3,P(x1,y1),Q(x2,y2),M(0,y3),N(0,y4).

联立椭圆与直线PQ方程,得(4k2+9)(x+2)2+24k(x+2)=0(Δ>0).

同解法2,利用韦达定理代入计算得MN的中点为定点(0,3).

把x+2看成整体以后,运算大大简化,这种简化的思想也是处理解析几何繁琐运算的常见思路.从代数的角度来看它是整体代换,从几何角度来看它的本质就是平移坐标系.

思路3：平移坐标系.

思路4：设线齐次化,将直线PQ方程代换.

对于lAP与lAQ,令x=0,可得MN的中点坐标为(0,k1+k2).

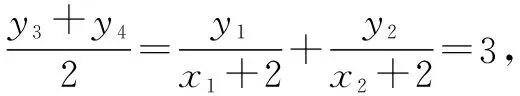
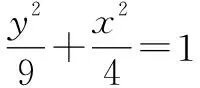
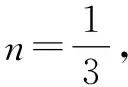
点评：利用平移、齐次化手段来解圆锥曲线中有关斜率之和或之积问题的理论基础是平移坐标系只是改变了点、曲线在坐标系中的位置,其几何属性如线段长度、直线斜率,直线间夹角都不会改变,但并不是所有圆锥曲线都适合平移、齐次化,只有涉及或者可以转化成两直线斜率之和、之积的问题才适合.方法虽好,但要慎用!

思路5：斜率同构或向量周构.

解法5：斜率同构.

设lAP:y=k(x+2),lPQ:y=t(x+2)+3,P(x1,y1),Q(x2,y2),M(0,y3),N(0,y4),且y3=2k.联立直线AP与椭圆方程,得(4k2+9)x2+16k2x+16k2-36=0(Δ>0),求出点P坐标再代入直线PQ方程,得12k2-36k+36t+27=0.设kAQ=k′,同理12k′2-36k′+36t+27=0,则k和k′是二次方程12x2-36x+36t+27=0的两个根,所以k+k′=3.故MN的中点为定点(0,3).

解法6：向量同构.

点评：思路5的两种解法同样是证明斜率之和为定值,却没有用到齐次化的方法,技巧性相对于解法4小很多,相当于寻找斜率满足的二次方程,也有同法可究.计算量也比前面几个解法小很多.

思路6：设点,利用点差法建立点M,N与点P,Q之间的关系.

解法7：设点法之点代法.

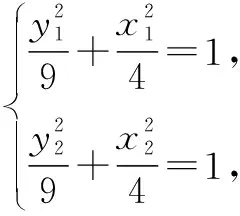
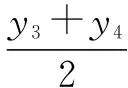
点评：解法7完全用点的坐标串联,设出点的坐标以后,寻求其满足的代数方程,通过代数方程的整体代换来实现定值的计算.

解法8：定比点差法.

思路7：极坐标设点.

解法9：角参法.

于是可得lPQ:2y(t1+t2)+3x(1-t1t2)=6(t1t2+1),代入点P坐标,得t1+t2=2.

思路8：曲线系法.

解法10：设lAP:x-my+2=0,lAQ:x-ny+2=0,lPQ:kx-y+2k+3=0,又椭圆在点A处的切线为x+2=0,因此过A,P,Q的二次曲线系为

解法11：极点极线法.

下附练习,供读者参考使用.

(1)求椭圆M的方程;

(2)直线l与椭圆M交于C,D两个不同的点(异于A,B),过C作x轴的垂线分别交直线AB,AD于点P,Q,当P是CQ中点时,证明:直线l过定点.

基于上述对试题的探讨研究,作出以下推广:

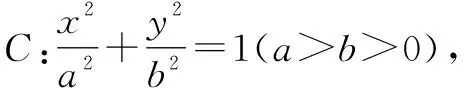
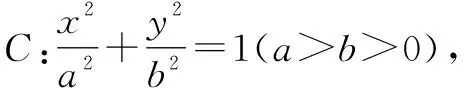
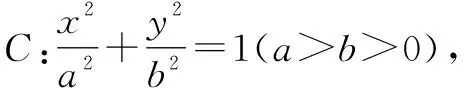
解析几何的相关问题对学生的基础能力、运算求解能力及应变能力要求较高,需要学生在平时的学习中学会归纳整理知识,建立各知识点之间的关系网,同时注重思维拓展,一题多解,提升能力.