匀强电场中电场强度的求解方法

文| 毛 雄

匀强电场中电场强度的求解是高中物理重要的知识，也是电学中的难点之一。文章介绍了在匀强电场中求电场强度的两种基本方法：等势面法和分解电场法。教师通过具体的例子说明了这两种解题方法的优点和缺点，使学生在遇到相关求电场强度问题时能快速解决。

匀强电场（Uniform Electric Field）是一种特殊的电场，其特点是场强在各个方向上都是相同的，且大小不随空间位置变化。在这种电场中，电势、电场强度和电场线具有以下特性：首先，在匀强电场中，电势与距离的关系是一次函数，即U=Ed，其中U 是电势，E 是电场强度，d 是沿电场线方向的距离。这意味着在匀强电场中，电势的变化率是恒定的。其次，匀强电场中的电场强度处处相同，用公式表示为E=F/q，其中F 是电场力，q 是电荷量。在匀强电场中，电场强度与电场力及电荷量无关，仅与电场的均匀程度有关。此外，在匀强电场中，电场线是相互平行的直线，且间距相同。这些直线代表了电场的方向和强度，线密度越大的地方电场强度越大。需要注意的是，电场线是为了形象化电场而假想的，实际上并不存在。匀强电场的基本概念和特性为我们分析和计算电场提供了便利。在求解匀强电场问题时，我们可以利用这些特性直接得到电场强度、电势等信息，从而简化计算过程。

等势面法和分解电场法是两种常用的求匀强电场强度的方法，它们可以帮助我们更好地理解和解决实际问题。以下是这两种方法的简要介绍：

等势面是指电势相同的各个点组成的面。在匀强电场中，等势面是一组相互平行的平面。通过找到这些等势面，我们可以更方便地分析和计算电场强度。等势面法的基本步骤：在已知电场强度的情况下，计算不同位置的电势；利用等势面的特性（即电势相同的点组成的面）找到这些等势面；利用等势面的分布，分析电场的性质和电场强度的变化。

分解电场法是将电场分解为多个简单的部分，分别计算这些部分的电场强度，最后将它们叠加得到总电场强度。这种方法可以帮助我们简化复杂的电场问题。分解电场法的基本步骤：将复杂的电场分解为多个简单的部分，如点电荷、线电荷、面电荷等；分别计算这些简单部分的电场强度；将这些电场强度按照矢量叠加原则进行叠加，得到总电场强度。

在实际应用中，我们可以根据问题的具体情况选择合适的方法。等势面法更适用于分析电场的分布和电势的变化，而分解电场法更适用于分解复杂的电场问题。综合运用这两种方法，我们可以更准确地求解匀强电场中的电场强度。

在高中物理中，我们知道电场线和等势面是相互垂直的。因为匀强电场的电场线是间隔均匀的直线，所以等势面也就是与电场线垂直的间隔均匀的直线。在中学阶段，我们在求匀强电场中电场的大小和方向时，常用的方法就是找等势面，根据等势面来求电场的大小和方向。

例1.一匀强电场平行于纸面，不知道电场的方向，用仪器沿互成60°角的OA、OB 两个方向探测，得知该静电场中各点电势φ 与到O 点距离的函数关系（如图1 所示）。

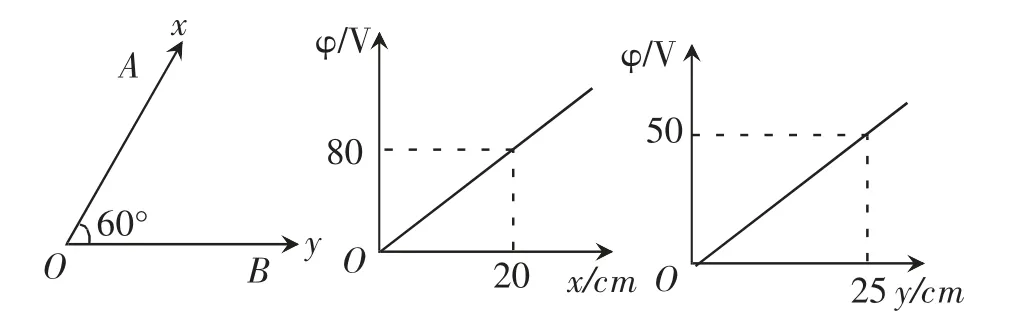
图1

下列说法中有关该电场的电场强度E 的说法中，正确的是（）

A.E=400V/m，沿AO 方向

B.E=200V/m，沿BO 方向

解法1：利用等势面法

如图2 所示，设OC=25cm，OF=20cm，D 点电势与C 点电势相等，则，由图1 可知，φF=80V，φC=50V，由以上各式解得OD=12.5cm，由几何知识可知CD⊥OA，CD 为等势线，由电场线与等势线垂直及沿电场线方向电势越来越低可知，电场方向沿AO 方向，电场强度A 正确，B、C、D 错误。

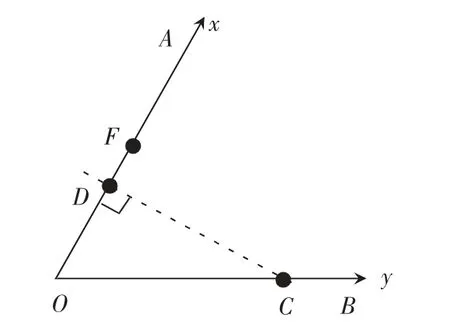
图2

解法2：利用分解电场法

分解电场法基本思路（如图3）：

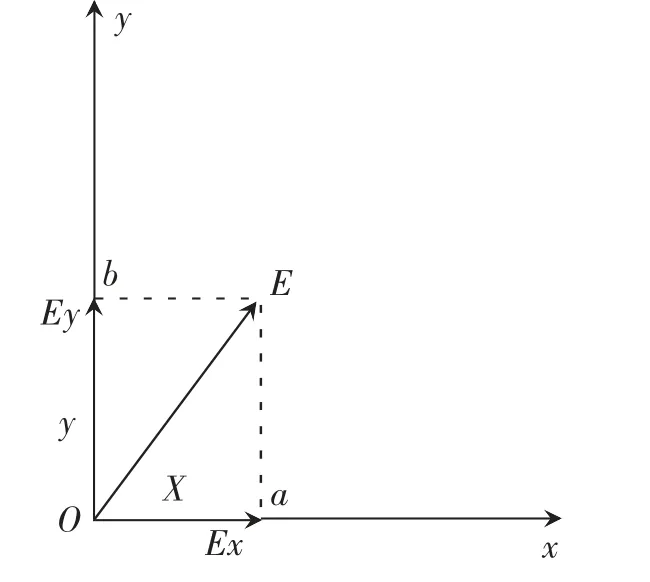
图3

UOa=Ex·x；UOb=Ex·y

Ex=Uoa/x；Ey=Uob/y，方向由高电势指向低电势。

例1 采用分解电场法如下解答：

A 中φ-x 图线的斜率表示电场强度E，结合图1可知，Ex=400V/m，Ey=200V/m，沿着电场线方向电势降低，故x、y 方向上的电场强度方向如图4 所示，由∠AOB=60°，易知图中虚线为等势线，则电场强度沿AO 方向（大小为E=Ex=400V/m）。由排除法可知，A项正确，B、C、D 三项错误。

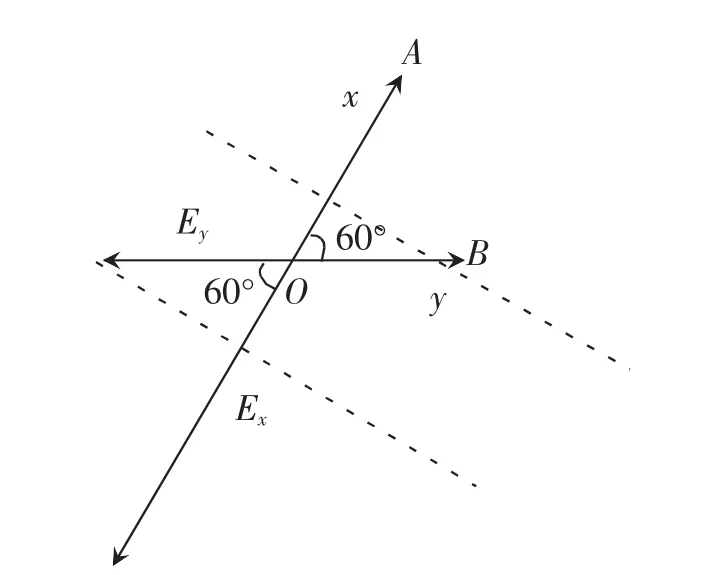
图4

利用等势面法和分解电场法并不是对所有解决匀强电场中电场强度的问题都是最简单的。

例2.如图5 在xOy 平面内有一匀强电场的方向平行于此平面，平面内有三个点a、b、c，其中a 点的电势为10V，b 点的电势为17V，c 点的电势为26V。以下说法正确的是（）

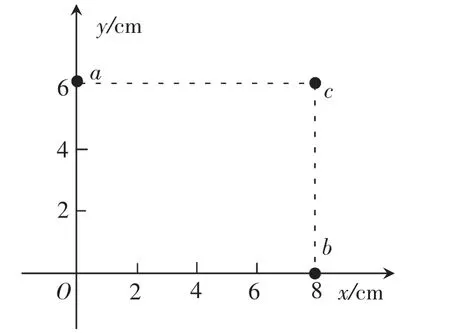
图5

A．此匀强电场的电场强度的大小为2.5V/cm

B．坐标原点O 处的电势为1V

C．有一电子从b 点出发运动到c 点，电场力做功为9eV

D．电子在a 点的电势能比在b 点的电势能低7eV

解析：如图6 所示，

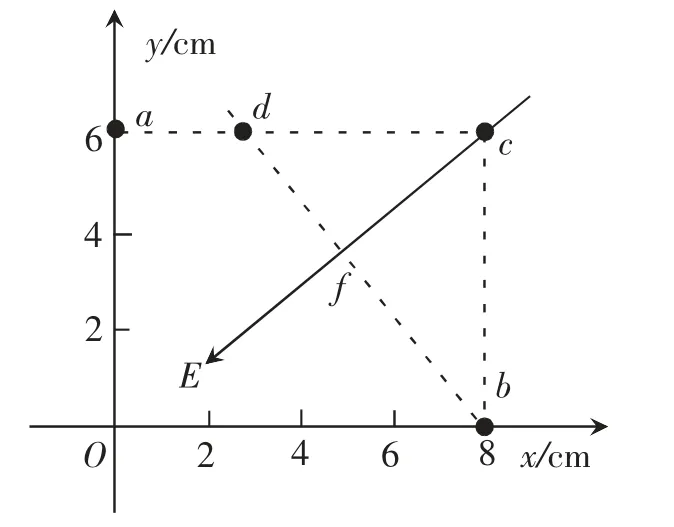
图6

对于这道选择题来说，要想快速且正确地解决这个问题，利用等势面法的运算量还是比较大，需要先确定d 点的位置，然后再计算cf 的长度，这样的操作对于学生来说容易出错。我们换成分解电场法，从题目中知道场强E 是矢量，是可以沿着两个垂直的方向分解的，就可以先求出沿x 轴、y 轴两个方向的分量，最后再用矢量合成的方法求出合场强的大小和方向。

如图6 所示，根据a、b、c 三点电势的大小可以知道O 点电势就是1V，根据电场强度的方向由高电势指向低电势可知：x 方向的场强沿x 轴负方向，大小，同理可知y 方向的场强沿y 轴负方向，大小所以合场强E=2.5V/cm，方向与y 轴负方向成53°。通过上面的分析可以确定本题的答案为A。

显而易见，对于此问题我们用分解电场法显然比等势面法要简单且快速。

例3.如图7 所示，在匀强电场中，三角形ABC为正三角形，三角形的边长为2 cm，已知UBA=4V，UCA=2V，求场强的大小和方向？

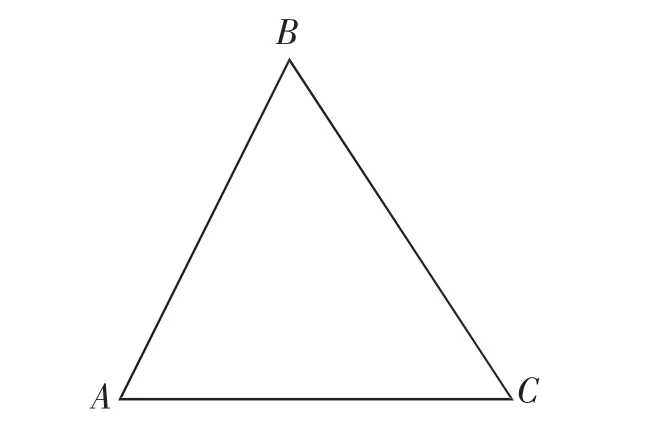
图7

解析：这道题如果用分解电场的方法进行解答，需要把电场分为BA 方向和CA 方向，分别求两个方向电场的大小，再进行矢量合成的话就不正确了。下面我们用等势面法计算。

如图8 所示，电势分别为φA=2V，φB=4V，φC=6V，由匀强电场性质可知，AB 中点D 的电势为2V，连接CD 则为等势线，BA 垂直于CD，所以BA 为电场线。理由是沿着电场线的方向电势逐渐降低，因此，场强的方向由B 指向A，大小在这里用等势面法快速地找到了问题的答案。

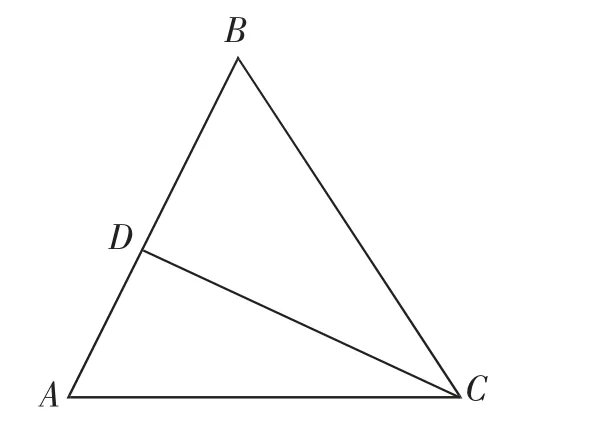
图8

由此可以看出，等势面法解这道题更简单。上面用分解电场的方法为什么会出错呢？

这是因为如果不是按照两个互相垂直的方向分解电场，这两个电场会在另一个方向产生电势差。如BA 和CA 方向分解电场，BA 方向的分量会在CA 方向产生电势差，同时CA 方向的电场会在BA 方向产生电势差，这样我们的表达式就应该表示为：

最后解得EBA=2V/cm，ECA=0，电场的方向由B 指向A。

总结：等势面法和分解电场法是我们在解决匀强电场中电场大小和方向问题时经常用到的方法，到底用哪种方法更简单便捷，要具体问题具体分析，选择简便灵活的方法，这就需要教师在解决问题的时候，善于归纳总结，让教学和学习变得轻松愉快！