基于Origin的一维电荷分布系统的静电场模拟
钱宏明,张季谦
(1.马鞍山师范高等专科学校 软件与食品工程系, 安徽 马鞍山 243000;2. 安徽师范大学 物理与电子信息学院, 安徽 芜湖 241000 )
基于Origin的一维电荷分布系统的静电场模拟
钱宏明1,张季谦2
(1.马鞍山师范高等专科学校 软件与食品工程系, 安徽 马鞍山 243000;2. 安徽师范大学 物理与电子信息学院, 安徽 芜湖 241000 )
摘要:以几种一维电荷分布系统为例,推导出它们的电场线方程及等势线方程,利用Origin软件的矩阵功能建立表征电场线及等势线分布的数据矩阵,再利用Origin的绘图功能绘制出电场线和等势线的仿真图形。结果表明,用Origin模拟静电场无需编程、简单易用,所得仿真图形准确、美观。仿真模拟既可以为静电场的课堂教学提供直观便利的认识,弥补传统教学手段的不足,又可以进一步加深学生对静电场分布规律的理解。
关键词:Origin;一维电荷分布系统;电场线;等势线;仿真图形
电场强度E和电势U是表征静电场特性的两个基本物理量,为了将抽象的静电场形象化、具体化,常采用电场线和等势线(面)来描绘静电场[1]。但静电场中没有电流,无法用仪表直接测量,实验室中主要用稳恒电流场来模拟静电场[2],耗时长且易受到实验仪器等因素的影响,很难得到精确结果。近年来,随着计算机软件技术的发展,人们开始用数值计算软件来模拟静电场,比较常用的是Matlab,例如王明美[3]模拟了点电荷对的电场线和等势线,谢宁[4]绘制出了几种一维电荷分布系统的电场线,孙祥鲲等[5]构建了平面点电荷系的电势与电场强度矢量图。使用Matlab软件虽然有助于揭示静电场的性质,但使用Matlab软件需要具备一定的计算机编程能力和矩阵知识,还要熟悉大量的函数和命令,而作为同样功能强大的数据分析和图形可视化软件,Origin的使用更加简便,只需点击鼠标结合菜单命令便可完成大部分操作[6]。本文主要介绍在教学过程中,如何巧妙利用Origin软件的绘图功能,简洁便利地展示静电场的分布规律和特点,以便让学生快速、直观形象地掌握这种抽象物理概念,从而提高课堂教学效果,激发学生学习的积极性。
1原理与方法
1.1基本原理
在平面直角坐标系中,电场线和等势线的微分方程可以分别表示如下
(2)
根据(1)式、(2)式,结合场强叠加原理和电势叠加原理可推导出图1中几种一维电荷分布系统的电场线方程和等势线方程[1,7]。
1.1.1点电荷对
电场线方程:
(3)
等势线方程:
(4)
1.1.2共线3点电荷系统
电场线方程:
(5)
等势线方程:
(6)
1.1.3有限长均匀带电直线
电场线方程:
(7)
等势线方程:
(8)

图1 几种一维分布电荷系统模型。
1.2仿真方法
启动Origin8.5,新建Matrix(矩阵),选择菜单命令“Matrix|SetDimension/Labels” 打开“MatrixDimensionandLabels”对话框,设置矩阵行、列范围以及x、y的起止坐标;再选择菜单命令“Matrix|SetValues”打开“SetValues”对话框,根据电场线(等势线)方程在“Cell(i,j)=”文本框中输入函数,设置完成后单击“OK”确认,即可生成表征电场线(等势线)分布的数据矩阵;最后通过“Plot”菜单便可选择绘制2D、3D等多种图形,由“File|ExportGraphs”菜单命令还可导出各种格式的图片。
2仿真过程与结果讨论
(3)~(8)式中C均为常数,不同的取值对应不同的电场线和等势线,为了简化问题、方便比较,作无量纲处理,并统一设置矩阵为500×500, 坐标统一设定为:-4≤x≤4、-4≤y≤4。
2.1点电荷对
2.1.1同号异量点电荷对
设定参数:q1=1、q2=3、l=1,根据(3)式在矩阵元值窗口输入:(x+1)/sqrt[(x+1)^2+y^2]+3*(x-1)/sqrt[(x-1)^2+y^2)],根据生成的数据绘制黑白线条等高线图即可得到电场线的平面分布图,若对所得图形效果不满意,可以双击图形区域,在弹出的“PlotDetails”对话框中通过修改或增减常数来调整电场线的条数和密度,最终效果如图2(a)所示。再建立一个矩阵,根据(4)式对矩阵元值进行函数设置: 1/sqrt[(x+1)^2+y^2]+3*1/sqrt[(x-1)^2+y^2)],同样可得等势线的平面分布图,如图2(b)所示。利用Origin的图层功能可以将两个不同数据矩阵绘制的图形链接到同一坐标中,如图2(c)所示。

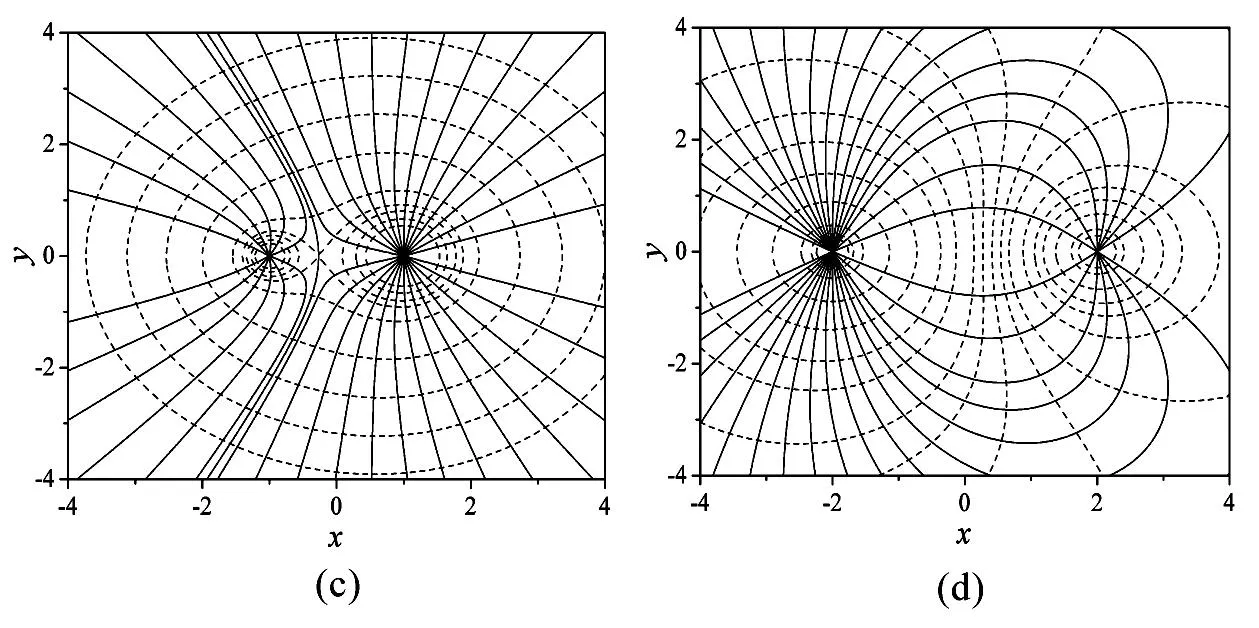
图2 点电荷对电场仿真图形。
2.1.2异号异量点电荷对
改变参数,取q1=-2、q2=1、l=2,用相同方法可得异号异量点电荷对的电场线和等势线的仿真图形,如图2(d)所示。若取q1=±q2即为人们所熟悉的等量同号(异号)电荷的电场情况,这里不再讨论。
2.2共线3点电荷系统
2.2.1对称分布的3点电荷系统
设定参数: q1= q3=2、q2=1、l1= l2=1,建立两个矩阵,根据(5)、(6)式对矩阵元的值分别进行函数设置: 2*(x+1)/sqrt[(x+1)^2+y^2]+x/sqrt(x^2+y^2)+2*(x-1)/sqrt[(x-1)^2+y^2],2/sqrt[(x+1)^2+y^2]+1/sqrt(x^2+y^2)+2/sqrt[(x-1)^2+y^2]。将由两个数据矩阵绘制的图形置于同一坐标中,得到图3(a)。 通过绘图菜单还可以根据所得数据绘制3D图形,如图3(b)所示。

图3对称3点电荷系统电场仿真图形(q1=q3=2、q2=1、l1=l2=1)。
(a)电场线(实线)和等势线(虚线)平面分布图; (b)电势三维曲面分布图。
2.2.2非对称分布的3点电荷系统
方法同上,重新设定参数,得到非对称分布的3点电荷系统的电场分布, 如图4、图5所示。
2.3有限长均匀带电直线
取 l =1,根据(7)、(8)式在两个矩阵的矩阵元值窗口分别输入:sqrt[(x+1)^2+ y^2]-sqrt[(x-1)^2+y^2],{sqrt[(x+1)^2+y^2]+x+1}/{sqrt[(x-1)^2+y^2]+x-1},得到均匀带电直线的电场仿真图形,如图6所示。
3结语
本文根据电场线方程和等势线方程,结合Origin的数据分析和制图功能,得到了点电荷对、共线3点电荷、均匀带电直线的电场线和等势线的计算机仿真图形。结果表明,用Origin模拟静电场,具有操作简便、结果准确、图形美观等特点,可以为静电场的理论分析和实验教学提供便利。理论上,本文的方法同样适用于其他已知电场线方程和等势线方程的带电体,也可用于光学实验[8-9]的仿真模拟。

(a) (b)
图4位置对称、电量不对称3点电荷系统电场仿真图形(q1=2、q2=q3=-1、l1=l2=1)。
(a)电场线(实线)和等势线(虚线)平面分布图; (b)电势三维曲面分布图
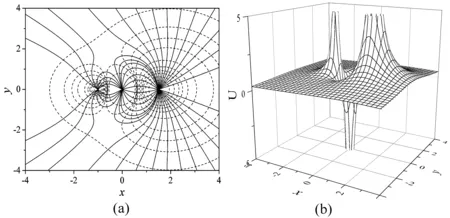
图5 位置、电量都不对称三电荷系统电场仿真图形(q1=1、q2=-2、q3=3、l1=1、 l2=1.5)。

图6 有限长均匀带电直线的电场线(实线)和等势线(虚线)平面分布图。
参考文献:
[1] 程守洙,江之永.普通物理学(第二册) [M]. 北京:高等出版社,1998:3-29,46-61.
[2] 杨述武. 普通物理实验(第二册) [M]. 北京:高等出版社,2000:59-65.
[3] 王明美.一对点电荷的MATLAB模拟实验[J].合肥师范学院学报,2010,30(3):40-43.
[4] 谢宁.一维电荷分布系统的电场线[J].大学物理,2007,26(6):5-10.
[5] 孙祥鲲,原力格,杨宏伟.基于MATLAB构建点电荷系的电势与电场强度分布图[J].实验技术与管理,2007,24(10):75-78.
[6] 周剑平.Origin实用教程[M]. 西安: 西安交通大学出版社,2007:1-6,145-177.
[7] 周益群,张智,刘凤翔.点电荷对、平行长直电荷对、有限长直电荷的电力线方程和等势线(面)方程[J].物理与工程,2004,14(2):26-29,42.
[8] 曹卫军,赖康荣. 基于Origin的波动光学实验仿真[J].大学物理,2015,34(1):49-52,69.
[9] 钱宏明. 用Origin实现夫琅禾费衍射现象的仿真[J].绵阳师范学院学报,2015,34(2):30-33,113.
Electrostatic Field Description of One Dimensional Charge Distribution System Based on Origin
QIAN Hong-ming1, ZHANG Ji-qian2
(1 Department of Software and Food Engineering,Ma′anshan Teacher’s College,Ma′anshan, Anhui 243000,China;2 College of Physics and Electronic Information,Anhui Normal University,Wuhu, Anhui 241000,China)
Abstract:Taking several one-dimensional charge distribution systems as an example, the electric field lines and potential linear equations are firstly deduced. Then, the data matrix of the distribution about these curves is established by using matrix function of Origin software. Finally, the graphics of these curves are drawn by using Origin. Our results show that it does not need to program for simulation by Origin, this method is simple and easy to use, and the simulation figures are accurate and beautiful. The simulation can provide an intuitive and convenient understanding to the classroom teaching of the static electricity field, thus this can be used for overcoming the shortcomings of the traditional teaching method. Furthermore, it can deepen the understanding of the distribution of the electrostatic field.
Key words:Origin, one dimension electric charge system, electric field line, equipotential curve, simulation graphics
文章编号:1007-4260(2016)01-0127-04
中图分类号:O441.1
文献标识码:A
DOI:10.13757/j.cnki.cn34-1150/n.2016.01.032
作者简介:钱宏明,男,安徽马鞍山人, 硕士,马鞍山师范高等专科学校软件与食品工程系讲师,主要研究方向为大学物理、非线性动力学。E-mail: qhm01984@126.com
基金项目:安徽省自然科研基金(1508085MA15)和安徽师范大学千人培养计划项目(2012020872)。
*收稿日期:2015-09-06
网络出版时间:2016-03-15 17:05网络出版地址:http://www.cnki.net/kcms/detail/34.1150.N.20160315.1705.032.html

