线电荷的电力线和等势线的MATLAB 作图
易学华,郭俊广,曹人平
(嘉应学院 物理与电子工程学院,广东 梅州 514015)
0 引言
在电磁学[1]和数学物理方法[2]的教学过程中,往往要画电力线和等势线.等量异号和等量同号的点电荷电力线[3-4]和直线电荷[5]以及带电球体[6]的电力线和等势线都比较好画,不等量的直线电荷对的电力线和等势线则比较麻烦,而用MATLAB[7]中函数则简单得多.将图形制成文件,插在教案中,对电磁学和数学物理方法教学很有帮助.
1 无限长直线电荷
1.1 直线电荷的电力线
真空中无限长带电直线的场强大小为

其中λ是线电荷密度,ε0是真空介电常数,r是场点P(x,y)到轴线的距离.电场呈轴对称分布.取λ>0,电力线是以轴线为起点的射线簇,各射线之间的夹角相同.
1.2 无限长线电荷的等势线
以某点为零势点,该点与轴线的相距为a,则场点P的电势为

等势面是以轴线为中心的圆柱面.取一个垂直于轴线的垂面,等势线就是一簇簇的同心圆.
设k=λ/(2πε0),取r0为第一条等势线的半径,其电势为

取ΔU为电势的增量,则相邻等势线的电势为U=U0+ΔU,该等势线的半径为

重复上述步骤,就能决定其他等势线的半径,相邻两条等势线的电势差都是相同的.图 1 表示正的直线电荷的电力线和等势线,电荷的线密度为λ=10-9C/m,a=1 m 处为电势零点;越往中心,电势越高,等势线也越密.
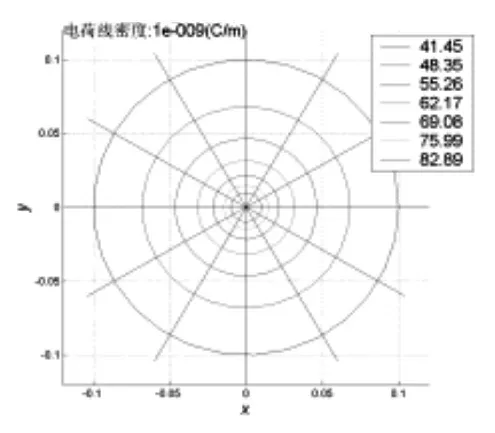
图1 带正电的直线电荷的电力线和等势线示意图
2 等量异号无限长直线电荷
2.1 电力线
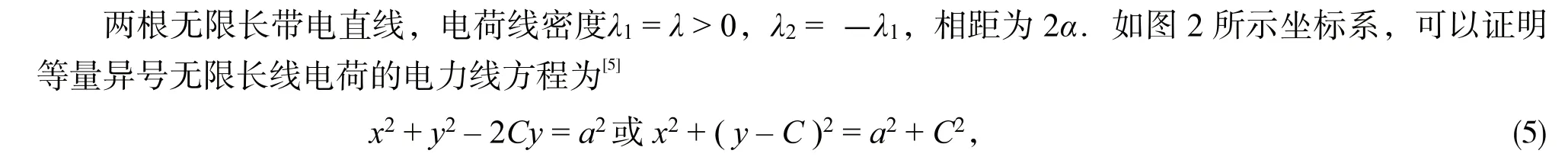
C是由起角决定的常数.由于电力线起始于正电荷,终止于负电荷,所以每条电力线都是一段圆弧,而上下两条对应的电力线形成一个圆.
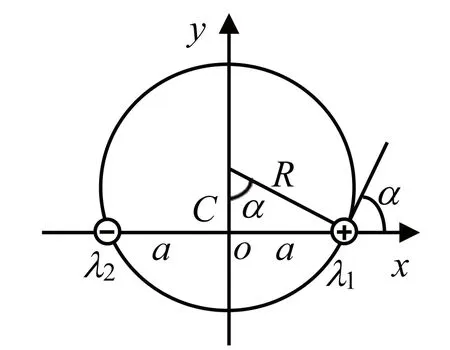
图2 等量异号无限长线电荷的电力线示意图
2.2 等势线
还可以证明,等量异号无限长线电荷的等势线方程为[5]

这也是一个圆,圆心在(C,0),其半径为

C是由电势或起始点决定的常数.
如图3 所示,第一条经过点P0(x0,0)的等势线的常数为
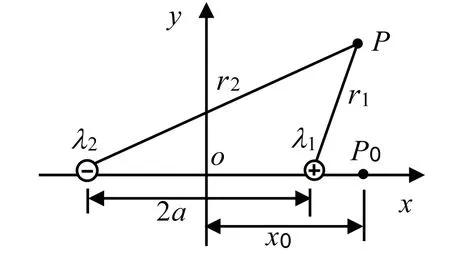
图3 等量异号无限长线电荷的等势线的起点示意图

由此可计算圆的半径,画出一条包围右边电荷的等势线.根据对称性,又能画出包围左边电荷的等势线.为了决定其他等势线的位置,先要计算第一条等势线的电势.取o点为零势点,由(2)式可知,两线电荷在场点P产生的电势为

将x代入(10)式就能计算新的常数C,然后由(9)式计算圆的半径R,从而画出新的等势线.其他等势线经过x轴的位置都能用这种步骤求出.等量异号无限长带电直线的电力线和等势线如图 4 所示,电荷的线密度为,两线相距2a=0.04 m.这些曲线是关于x轴和y轴对称的,中间的竖线是零势线,图例表示正电荷周围等势线的电势.

图4 等量异号无限长直线电荷电力线和等势线
3 等量同号无限长直线电荷
3.1 电力线
两无限长带电直线,电荷线密度λ1=λ2=λ>0,相距为2a.如图5 所示坐标系,可以证明,等量同号无限长直线电荷的电力线方程为


图5 等量同号线电荷的电力线起点示意图

3.2 等势线

等量同号无限长带电直线的电力线和等势线如图6 所示,这些曲线也是关于x轴和y轴对称的,经过原点的等势线是零势线.(x,0)就是新的等势线的起点坐标,用上述方法可以计算和画出新的等势线.

图6 等量同号线电荷的电力线和等势线
4 不等量无限长直线电荷
4.1 电力线
如图7 所示,两线电荷的线密度λ1和λ2不一定相等,相距2a,它们在场点P产生的场强分别为

图7 线电荷对的电场
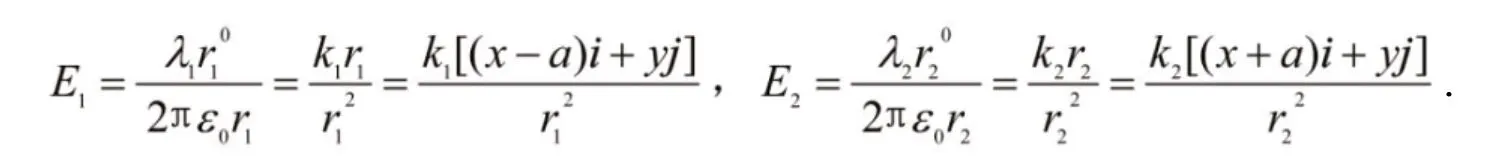

4.2 等势线

图8 不等量同号线电荷的电力线和等势线

图9 不等量同号线电荷的电力线和等势线
5 结语
如果电力线或者等势线能用为x或y的显式表示(包括圆),直接用表达式就能计算函数值法并画曲线.如果电力线不能用显式表示,用MATLAB 的ode 函数特别有效.当电势的变化规律比较复杂时,用等高线函数画等势线最简单.当两个线电荷等量时,用切线法和等高线法都能画出如图 4 和图6 所示的电力线和等势线.
用MATLAB 画电力线和等势线有很多优点,图形标准、精确、易于调整.将电力线和等势线的图片应用于数学物理方法[8]以及其它物理课程教学中,很能说明问题,对学生理解电力线和等势线的物理意义起到很重要的作用,能够更好地帮助学生学习抽象的数学物理方程.

