回归知识本质，感悟数学思想

仇学春

摘 要：多边形的面积是小学数学课程核心内容之一。《九章算术》是我国数学经典名著，其中关于土地面积计算的方法涉及不同的平面图形，一以贯之地体现了“以盈补虚”化归为长方形面积计算的思路，以及由特殊推及一般的数学思想方法，能为多边形面积公式推导的教学提供有益的启示。 由此，“多面形的面积”单元的教学有几点新思路：将对高的认识有机融入面积计算的过程，体现知识产生的内在合理性;推导三角形面积公式，体现化归方法的一致性和归纳的方法;推导梯形面积公式，体现化归方法的一致性和一般化方法;统一面积公式，建立二维空间观念。

关键词：《九章算术》；以盈补虚；多边形面积；公式推导

多边形的面积是小学数学课程的核心内容之一。这一内容的学习既是解决实际问题的需要，也有助于增强学生的空间观念和推理意识。学生在学习过程中能够从测量的角度深化对平面图形的认识，进一步感悟测量的基本方法。

现行小学数学教材关于多边形面积教学内容的编排，呈现的基本逻辑顺序是：长方形的面积→平行四边形的面积→三角形的面积→梯形的面积。其中，平行四边形面积公式的推导，引导学生将平行四边形剪拼成长方形（学生在认识平行四边形时已经认识了高，或者在推导多边形的面积公式之前单独认识了高）。而三角形和梯形面积公式的推导，则重点引导学生将两个完全相同的三角形或梯形拼成一个平行四边形。有的也呈现了将一个三角形或梯形剪拼成学过的图形推导面积公式的方法。学生将一个图形剪拼成已知图形来推导面积公式是有经验的，如将平行四边形剪拼成长方形。如果以方格作为面积单位，则更容易在数方格的过程中，想到将不满整格的凑成整格，从而发现可将平行四边形沿着高剪下一个三角形或梯形，拼成长方形，实现图形的化归。而在三角形、梯形面积公式的推导过程中，学生一般很难想到将两个完全一样的三角形或梯形拼成一个平行四边形。由于这样拼成平行四边形后推导面积公式的过程相对简单，所以教材都以这一推导面积公式的方法作为重点。那么，如何既顺应学生的认知现实，又回归多边形面积计算的本质，凸显面积计算方法的一致性呢？

《九章算术》是我国数学经典名著，其中关于土地面积计算的方法涉及不同的平面图形，一以贯之地体现了“以盈补虚”化归为长方形面积计算的思路，以及由特殊推及一般的数学思想方法，能为多边形面积公式推导的教学提供有益的启示。

一、《九章算术》中涉及的土地面积计算方法及其教学启示

《九章算术》的《方田章》主要涉及“以御田畴界域”的问题，给出了长方形、三角形、梯形等直线形的面积公式。

第一，长方形的面积。“方田术曰：广从步数相乘得积步。”［1］方田即长方形田，“广”为东西的度量，“从”为南北的度量。这里以“步”作为长度单位，积步相当于平方步，即为面积单位。

第二，三角形的面积。“术曰：半广以乘正从。半广知，以盈补虚为直田也。亦可半正从以乘广。”［2］《九章算术》中的圭田，通常指三角形田，也有人认为指等腰三角形田。“以盈补虚为直田也”，意指将图1中的Ⅰ、Ⅱ分别移至Ⅰ′、Ⅱ′。

第三，梯形的面积。对于直角梯形，《九章算术》称为“邪田”，“邪”指直角梯形中的斜边。“术曰：并两邪而半之，以乘正从若广。又可半正從若广，以乘并……并而半之者，以盈补虚也。”［3］如图2，“两邪”指与“邪”相邻的两广或两从。“以盈补虚”的方式如图3，将Ⅰ移至Ⅰ′即可。

对于一般梯形，《九章算术》称为“箕田”（如图4）。“术曰：并踵、舌而半之，以乘正从……中分箕田则为两邪田，故其术相似。又可并踵、舌，半正从，以乘之。”［4］《九章算术》认为，将箕田中分，成两邪田（如图5）。

图形测量的重点是确定图形的大小，一维图形的大小是对图形长度的度量，二维图形的大小是对图形面积的度量，三维图形的大小是对图形体积的度量。图形成为数学研究对象的真正动力，是土地测量等生产实践。《九章算术》中的土地面积计算方法对多边形面积公式推导教学有颇多启示，主要体现在方法逻辑维度。

《九章算术》在土地面积计算的过程中重视体现化归和一般化的数学思想方法。化归的思路是：以长方形的面积计算为基础，将三角形化归为长方形，将直角梯形化归为长方形。化归的方法是：以盈补虚。在梯形的面积计算中，化归的思路是灵活的：直角梯形化归为长方形，而一般梯形则化归为直角梯形。另外，先研究直角梯形的面积计算方法，再过渡到一般梯形，体现了由特殊到一般的思想方法。

这给我们的教学启示是：（1）化归的目标指向长方形。长方形的面积计算方法在多边形中是最简单的，因为它很容易由面积单位的度量这一基本方法优化得到，最便于学生体会多边形的面积是二维属性的度量。都归为长方形这一基本图形，能够更好地凸显面积计算方法的本质，即平面图形的面积是二维属性的度量，与两个维度相关。（2）化归的方法是“以盈补虚”。平面图形之间的联系十分丰富，彼此之间化归的方式也是多样的。如三角形可以通过“以盈补虚”化归成长方形，也可以“加倍拼接”化归成平行四边形。其中，“以盈补虚”的方法是实现图形化归的基本方法，也体现了度量的运动不变性。

需要注意的是，现行教材中三角形面积计算方法的得出，主要是引导学生通过将两个完全相同的三角形拼成一个平行四边形发现的。这样的方法对于学生而言，与其头脑中自然形成的关于测量的运动不变性认识存在“隔阂”（因为改变了测量对象的面积），需要进行很多铺垫和引导。学生的已有知识经验仍然是“以盈补虚”，教学时要基于这一知识经验帮助他们实现图形的化归，而不能因为某种方法容易操作就“强加”给他们。另一方面，在引导学生探索图形面积计算的方法时，又要根据图形的具体特点和内在联系，感受化归方法的多样性，发展思维的灵活性。也即，可以把锐角三角形、钝角三角形分成两个直角三角形，把梯形分成两个三角形计算面积。这样的方法体现了测量的有限可加性，也是学生容易理解的方法。

二、“多边形的面积”教学思路新探

由此，苏教版小学数学五年级上册“多边形的面积”单元的教学，有以下几点新思路：

（一）将对高的认识有机融入面积计算的过程，体现知识产生的内在合理性

现行教材对高的认识有两种处理方式：一是在认识多边形时将高作为认识图形的内容进行教学；二是在教学多边形的面积公式前先安排一课时，认识各种多边形的高。在认识多边形时认识高，学生可能缺乏认知的心理需求，因为高并不直接构成多边形的组成要素，多边形高的特征往往表现为多边形边和角的特征。在教学面积公式前认识高，符合知识之间的逻辑顺序，测量多边形的面积需要测量高，所以在学习面积测量之前应先认识高。但如何解决学生的认知需求问题，仍是难点。将对高的认识融入面积计算的问题解决过程中，可以体现知识产生的内在合理性，是一条可行的教学思路。

高和底是一组相关联的概念。平行四边形的高和底，三角形的高和底，梯形的高和上底、下底分别共同决定了各个图形面积的大小。为了引导学生产生认识高的需求，应将高的认识有机融入各种多边形面积公式的教学过程。突破这一认知的起点和关键是平行四边形的面积计算。教学时可用细木条做一个可拉动的平行四边形框架，由长方形逐渐拉扁，体会边长不变，但水平方向对边的距离逐渐缩短，面积逐渐变小；反之亦然。平行四边形面积的变化如图5所示。

（二）推导三角形面积公式，体现化归方法的一致性和归纳的方法

在推导三角形面积公式时，以学生容易理解的“以盈补虚”方法为主，而将两个完全相同的三角形拼成平行四边形的方法作为练习处理。“以盈补虚”的方法和平行四边形的面积计算方法是一致的，学生容易理解，也容易发现。 “以盈补虚”的方法将三角形化归为长方形，容易凸显三角形的面积也与底、高两个元素相关。如果采用将两个完全相同的三角形拼成一个平行四边形的方法，则和学生已有的认知经验不一致，且不符合测量的基本原理。

考虑到三角形分为直角三角形、锐角三角形和钝角三角形三类，按照由易到难的顺序，可以分别探索直角三角形、锐角三角形和钝角三角形的面积公式。这样做的优势在于：直角三角形化归为长方形最容易；锐角三角形和钝角三角形可以作一条高，化归为两个直角三角形，也可以化歸为一个长方形，体现了思维方法的灵活性。这样的思路也体现了归纳的方法。

（三）推导梯形面积公式，体现化归方法的一致性和一般化方法

按照由易到难、由特殊到一般的顺序，先教学直角梯形的面积计算，鼓励学生自己探索多样的方法，重点关注“以盈补虚”的方法，以进一步体会底和高决定梯形的面积大小，增强二维的空间观念。再教学一般梯形的面积计算，鼓励学生灵活运用多种方法，重点关注化归为两个直角梯形的方法，体会图形之间的内在联系。

（四）统一面积公式，建立二维空间观念

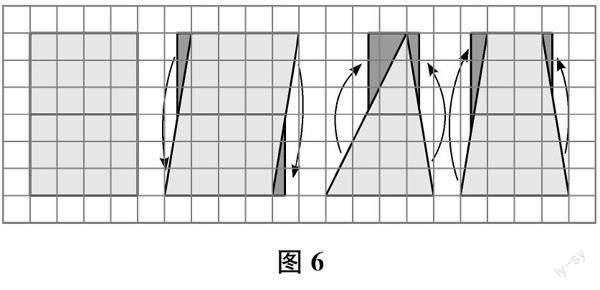
上述推导多边形面积公式的过程，始终围绕图形中非水平位置边的中点进行分割，实现“以盈补虚”（如图6所示）。因此，可引导学生体会这些多边形的面积具有统一的公式：多边形的面积=中位线×高。

这一内容可以作为一个弹性的教学活动。一方面，这样的认识有助于学生体会“以盈补虚”作为一般的推导多边形面积公式方法的意义。另一方面，统一多边形面积公式有助于学生更清晰地建立二维空间观念，并可将计算二维图形面积的方法经验迁移到计算三维柱体体积的过程中（柱体的体积=截面的面积×高）。

以上教学思路，是一次尝试，让《九章算术》与“多边形的面积”教学完美结合；也是一次突破，运用“以盈补虚”从定性和定量的维度解决了多边形面积公式教学的难点；更是一种创新，既满足了学生解决问题的需求，也有助于增强学生的空间观念和推理意识。

参考文献：

［1］［2］［3］［4］  郭书春.九章算术译注［M］.上海：上海古籍出版社，2009：13，35，37，38.

*本文系江苏省教育科学“十四五”规划一般课题“双螺旋互动：小学数学主线问题教学模型的开发与研究”（编号：D/2021/02/554）的阶段性研究成果。