一以贯之 上联下延
——从苏科版与人教版“整式的加减”教材对比谈起
高凯亮
(南京江北新区浦口外国语学校,江苏 南京 210031)
古往今来,从整体视角思考问题是广受推崇的方式之一,这种思考问题的方式有助于认清问题本质,从源头上解决问题[1].近几年,各地区积极开展大单元教学、结构化教学、整体教学,这些教学理念的核心思想都将问题指向如何帮助学生从整体上把握学习内容,避免知识碎片化.整体教学成功的关键在于如何从整体视角下精准解读教材、如何设计整体化的课堂活动、如何设计促进学生形成结构化知识的课后作业,以达到一个相对完整的整体教与学的过程.笔者对比苏科版、人教版教材“整式的加减”模块内容,获取一些有价值的思考,并在实施整体教学后进行总结与反思.
1 整体视角下两种教材“整式的加减”相关内容比较
1.1 课题名称、教学内容的比较
整式的加减是“数与代数”领域的重要内容,两种教材都将该内容编排在七年级上册.如表1所示,从章课题名称来看,苏科版、人教版教材分别用“代数式”“整式的加减”作为章课题名称.从每课时的课题名称来看,苏科版教材将每节课学习的内容作为每课时的课题;人教版教材用“整式”“整式的加减”作为每课时的课题,将本章问题直接指向要研究的对象(整式)及研究的内容(加减运算),对本章研究的问题更为聚焦.从总课时来看,两种教材“整式的加减”所处章节相差3课时,苏科版教材比人教版教材多设置了“用字母表示数”“数值转换机”“合并同类项练习课”这3个课时的内容.人教版教材章引言中说明:在小学,我们学过用字母表示数,知道可以用字母或含有字母的式子表示数和数量关系,这样的式子在数学中有重要作用.因此,人教版教材没有在本章节设置该内容.从教学内容来看,两种教材的差异不大.

表1 苏科版、人教版教材章课题、课时课题名称
1.2 两种教材“整式的加减”章引言、情境引入的比较
章引言是本章教学实施的引导,有助于师生准确把握本章教学方向.苏科版教材的章引言用“火柴棒搭小鱼”“日历”这2个情境引入,并且在章引言最后明确提出本章要研究用字母表示数、代数式以及整式的加减运算;人教版教材的章引言以行程问题为背景,提出3个实际问题.对比两种教材“整式的加减”模块每个课时的情境引入发现,两种教材都侧重于从生活情境引入,苏科版教材3个课时的情境引入是相互独立的,而人教版教材3个课时的情境引入是相互关联的.
综上所述,无论是从章课题名称还是从每个课时的情境引入来看,人教版教材的设计都具有较好的整体性,苏科版教材将每节课学习的内容作为该课时的课题,更有助于学生在课前自主预习时能快速精准定位本节课的主要学习内容,两种教材的设计各有权衡与侧重.值得注意的是,人教版教材在该章出现“类比数的运算”这句话共计2次,分别是在“合并同类项”“去括号”这2个课时中;人教版教材在第一课时课堂小结中得到“用字母表示数,字母和数一样可以参与运算”;实际上,人教版教材在该章渗透数式通性思想共计3次.苏科版教材虽然并未直接说明“类比数的运算”,但是在研究“合并同类项”“去括号”这2个课时的过程中都运用了乘法分配律.两种教材在这个章节都非常重视渗透数式通性思想.由数到式,是从特殊到一般的研究路径,两种教材在“整式”章节都未忽视学生已经积累的“有理数”的学习经验.
2 整体视角下“整式的加减”教学思考
通过以上分析可见,两种教材都是从生活情境进行引入.从运算类型来看,合并同类项是特殊的“单项式+单项式”,去括号是特殊的“单项式×多项式”.由于学生已经具备了“有理数”的学习经验,本章节不妨从整式的加减运算类型进行引入,以数式通性思想为主线进行整体教学,为学生后续学习整式的乘法、分式的运算、二次根式的运算直接积累经验.整式的加减内容以数式通性思想为主线进行整体教学,为“式”的教学“开山辟路”,为学生学习“式的运算”创建“类比源”,这样有助于学生对知识的正迁移,对后续“式”的教学具有指引作用.下文笔者以数式通性思想为主线对“整式的加减”模块(合并同类项、去括号、整式的加减)进行整体教学设计,第一节统领课帮助学生构建出整式的运算类型,再进一步将问题聚焦到“尝试写出一些整式的加减算式”.从式结构的视角来看,“整式的加减”分为“单项式±单项式”“单项式±多项式”“多项式±多项式”.第一节课让学生明确“整式的加减”的研究对象及路径,体会学习“合并同类项”“去括号”的必要性与必然性.
3 整体视角下“整式的加减”模块教学设计
3.1 “合并同类项”教学设计
3.1.1 问题引入,形成概念
问题1上节课研究了整式,这节课会研究什么呢?(整式的运算.)
追问1-1从哪里获得的经验?(有理数的学习经验.)
追问1-2接下来,我们研究整式的运算.研究的对象是谁?研究的内容又是什么?
追问1-3整式的运算存在哪些类型呢?(加、减、乘、除、乘方.)
追问1-4应先研究5种运算中的哪种运算呢?为什么?(加法.教师形成结构化的板书,如图1.)

图1
追问1-5这节课我们研究整式的加减,请你先写出一些整式的加减算式,并尝试写出运算的结果.
师生活动教师投影学生写出的整式的加减算式,引导学生从“式结构”的视角进行分类,分为“单项式±单项式”“单项式±多项式”“多项式±多项式”(如图2).从式结构来看,“单项式±单项式”的结构最为简单,师生达成共识,本节课先研究“单项式±单项式”.
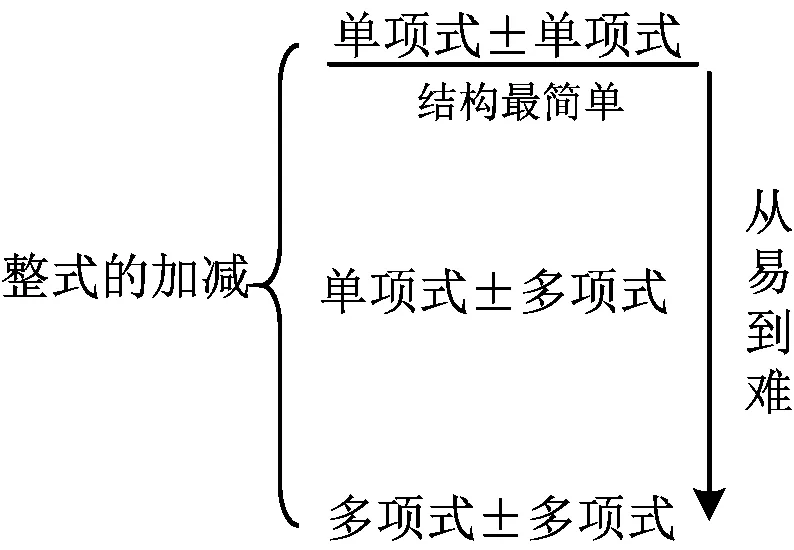
图2
(下文的素材来源于笔者执教时学生课堂生成的素材.)
教师投影学生素材:
1)2a+3a=5a;
2)2a2b+3ab2=5a3b3.
追问1-6第1个算式的结果正确吗?你能从生活视角给出直观的解释吗?你还能从其他视角进行解释吗?
追问1-7第2个算式的结果正确吗?如何说明?(引导学生用特殊值法验证.)
问题2你能借助图3说明“2a+3a=5a”的正确性吗?

图3
师生活动引导学生从整体与局部两个视角求出长方形面积,进而说明计算的正确性,培养数形结合思想.
3.1.2 例题精讲
例1合并下列各式的同类项.
1)y2x+3xy2;
2)-3x+2y-5x-7y;
尽管ADA推荐HbAlc≥6.5%便能对糖尿病进行诊断,但经该次研究得知,当HbAlc取值为6.34%、6.5%时,其诊断灵敏度与特异度较接近,表明当HbAlc于6.34%时,便可诊断DM。
3)a2-3ab+5-a2-3ab-7.

3.1.3 随堂练习
略.
3.1.4 课堂小结
通过本节课的学习,你有哪些收获?如何进行合并同类项?
3.1.5 部分作业设计
1)学习合并同类项有何价值?请举例说明.
2)下节课将会研究什么?如何研究?
设计说明本节课从数学内部发展进行引入,由一个“大”的核心问题引领,从“上节课研究了整式,这节课会研究什么呢?”展开,引导学生将“有理数”的学习经验正迁移至“式”的研究.由于七年级所学“有理数”包含加、减、乘、除、乘方这5种运算,根据“有理数”的研究经验,不断将问题聚焦到“整式的加减”.接下来,引导学生对“整式的加减”的类型进行分类,学生在活动中意识到有的单项式能相加(减),而有的单项式不能相加(减),这样引入的目的是让学生感受学习“合并同类项”“去括号”内容的必要性与必然性.为了后续快速确定几个单项式之间是否能相加(减),归纳出同类项的概念.本环节通过生活实例、乘法分配律及图形的面积共3个视角引导学生解释“2a+3a=5a”的合理性,培养学生的发散思维.此环节应用图形的面积验证结果的合理性是为了后续验证“整式的乘法”结果的合理性,为面积法推导乘法公式、证明勾股定理等知识奠定基础,培养数形结合思想.在例1的教学中,教师引导学生类比有理数的减法运算,将整式的减法运算转化为加法进行运算,渗透数式通性思想;在例2的教学中,教师先让学生自主尝试,展示学生不同的求值方法,比较直接代入求值与先化简再求值两种方法的优劣,引导学生感受学习合并同类项的价值所在.课后作业设计了2个问题,目的是让学生感受学习合并同类项的价值,并对下一节课的知识进行展望,培养学生“饮水思源”的意识.
特别说明,笔者执教时发现:学生在解释“2a+3a=5a”的合理性时,能够从生活视角给出多种解释,他们习惯将a看成具有同种属性的物体.例如,2个苹果加3个苹果等于5个苹果;学生还自主提出如果是2a+3b就不能加了.例如,2个苹果加上3个香蕉就不能加了,因此2a+3b不能合并.学生通过列举生活实例,借助生活经验去理解怎样的2个单项式才能相加,同类项概念的形成自然是水到渠成.这种借助生活经验思考问题的方式值得鼓励.
3.2 “去括号”教学设计
3.2.1 问题引入,探究法则
问题3上节课研究了“单项式±单项式”(投影上节课的板书图2),本节课继续研究“单项式±多项式”,请你写出一些“单项式±多项式”,并尝试写出结果.
追问3-1计算的困难在哪儿?(去括号.)
接下来,我们先研究去括号.
追问3-2请尝试写出下列各式的结果,并解释结果的正确性.
1)+(a-b)=______; 2)-(a-b)=______.
追问3-3总结去括号时符号变化的规律.
问题4尝试写出100-c(a+b)去括号后的结果,你是如何计算得到的?图4是面积为100 cm2的长方形,你能借助该图说明结果的正确性吗?
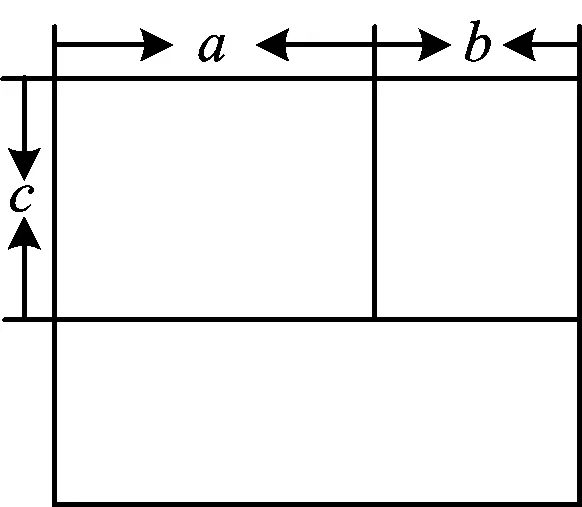
图4
3.2.2 例题精讲
例3化简下列各式:
1)5a-(2a-4b);
2)2x2+3(2x-x2);
3)6(m+n)-3(-m+2n);
4)(x+2y)-2(-x-2y).

3.2.3 随堂练习
略.
3.2.4 课堂小结
通过本节课的学习,你有哪些收获?去括号的依据是什么?
3.2.5 部分作业设计
1)学习去括号有何价值?请举例说明.
2)下节课会研究什么?怎么研究?
设计说明本节课是对第一节课“单项式±单项式”研究问题的延续,引入时直接投影上节课的板书(图2),立即将问题聚焦到本节课的核心内容(去括号),同时也让学生感受到去括号的必要性,通过问题2培养学生运用数形结合思想解决问题的能力.计算例题时,部分学生用去括号法则,部分学生用乘法分配律,只要学生能够运算正确,教师都应当鼓励.学生能够明确去括号法则与乘法分配律的本质联系即可,即去括号法则是乘法分配律演绎推理的结果.在例2教学中,教师先让学生独立尝试,评讲环节与第一节课一样,还是先展示不同的求值方法,比较直接代入求值与先化简再求值两种方法的优劣,带领学生感受去括号的价值所在.
3.3 “整式的加减”教学设计
3.3.1 问题引入,探究法则
问题5上节课研究了“单项式±多项式”(投影图2),本节课继续研究“多项式±多项式”,请你写出一些“多项式±多项式”算式,并尝试写出结果.
师生活动学生先写出算式后尝试计算出结果,然后总结出整式加减法则:一般地,几个整式相加减,如果有括号先去括号,再合并同类项.
3.3.2 新知应用,解决问题
例5笔记本的单价是x元,圆珠笔的单价是y元.小红买了3本笔记本、2支圆珠笔,小明买了4本笔记本、3支圆珠笔.买这些笔记本和圆珠笔,小红和小明一共用了多少钱?
例6做大、小两个长方体纸盒,尺寸如表2所示:

表2 长方体纸盒尺寸(单位:厘米)
1)做这两个纸盒共用料多少平方厘米?
2)做大纸盒比做小纸盒多用料多少平方厘米?
3.3.3 随堂练习
略.
3.3.4 课堂小结
通过本节课的学习,你有哪些收获?回顾“整式的加减”的研究路径.
3.3.5 部分作业设计
类比“整式的加减”研究路径,尝试研究整式的乘法.
设计说明本节课是对“合并同类项”“去括号”研究问题的延续,引入时直接投影第一节课的板书(图2),立即将问题聚焦到本节课的核心内容(多项式±多项式),通过问题1引导学生总结出整式的加减运算法则.本节课的例题主要是应用整式的加减解决问题.课后作业设计了一个微专题研究,类比“整式的加减”研究路径,尝试研究整式的乘法.教师批阅作业时要特别关注学生是否能够将“整式的加减”的研究经验正迁移至“整式的乘法”.例如,学生是否能够将“整式的乘法”的运算类型全部写出来,能否借助“有理数”的学习经验正确计算出结果等.
4 总结与反思
4.1 一以贯之,上“联系”学习经验
认知主义心理学家奥苏贝尔认为,一切有意义的学习都是在原有认知结构的基础上产生的,即一切有意义的学习必然包括迁移.教师在备课时需要考虑学生已有的学习经验或生活经验,课堂上引导学生将旧知进行正迁移,知识迁移过程中学生会无意识地将旧知与新知建立联系,促进整体教学目标达成.例如,上文以数式通性思想为主线对“整式的加减”模块(合并同类项、去括号、整式的加减)进行整体教学设计,在第一课时教学设计中设置追问“从哪里获得的经验?”“整式的运算存在哪些类型呢?”“应该先研究5种运算中的哪种运算,为什么?”,让学生在最初建立“整式的加减”的研究路径时就强烈感受到“数”的学习经验可以迁移至“式”的研究中,这是学习经验的迁移,更是教师对学生学习方法的指导,为学生可持续学习“式的运算”奠定基础.
4.2 一以贯之,下“延至”学习方法
整体教学的最大价值在于能够帮助学生从整体上把握学习内容,从整体视角分析问题,这样有助于学生掌握一类数学对象的研究路径及方法.方法的形成需要经验的积累.综观整体教学的全过程,教师在设计每课作业时,要有意识地设计能够帮助学生从整体视角思考的问题.例如,笔者在“整式的加减”整体教学中,前两节课的作业都让学生思考“学习合并同类项(去括号)有何价值?请举例说明”“下节课会研究什么?怎么研究?”,其目的是让学生感受到本节课学习的新知能解决什么问题,以及下节课该如何更进一步地研究整式的加减.第3课时其中一项作业是类比“整式的加减”研究路径,尝试研究“整式的乘法”,目的是逐渐引导学生形成从整体视角思考问题的习惯.若整体教学课后作业中没有提供从整体视角去“悟”的载体,则有点遗憾.
4.3 以教材对比、教材整合为抓手,助力实施整体教学
整体教学的前提是需要先将课时教学内容进行系统构建.课前进行“教材对比”“教材整合”,有助于教师从整体上把握教学的内容.在中国知网以“教材对比”为主题检索近10年的文献发表数量如图5所示.

图5
2017年后该主题文献数量增长速度较快,越来越多的学者认为“教材对比”是研究问题的重要手段之一.
例如,对比两种教材“整式的加减”模块内容发现,苏科版教材“合并同类项”第一课时中的例题没有涉及“先化简再求值”,人教版教材涉及该内容.由于笔者所在地区使用的是苏科版教材,因此,笔者将两种教材有机结合,在该课时增加一个“先化简再求值”问题.题目未必需要多难,目的是让学生感受学习合并同类项的价值所在,体会本节课的知识能解决哪些问题.对比两种教材“整式的乘法”模块发现,两种教材都是从整体与局部计算同一个长方形的面积进行引入,进而归纳总结出“单项式×单项式”“单项式×多项式”“多项式×多项式”法则.上文中笔者以数式通性思想为主线对“整式的加减”模块进行整体教学设计,但是并未忽视渗透数形结合思想,每课时教学中都有意识让学生从“形”的角度说明整式的加减结果的合理性,体现出数学课程的整体性与连续性.七年级初期阶段渗透从“数”与“形”两个视角思考问题是非常有必要的,能为培养学生创造性思维播下一颗种子.
5 结束语
总之,整体教学需要教师从整体视角理解教材,教师要站在教材编写者的角度思考问题,创造性地使用教材,尊重教材而不囿于教材,凭借教材又要跳出教材.在组织教学活动时,帮助学生向上联系学习经验,向下延伸至学习方法.整体教学教的是结构,学生学的是研究问题的方法,这能够为他们自身可持续发展奠定基础.

