凸显数学核心素养 呈现上游命题系统
成鸣娟
(西安电子科技大学附属中学太白校区,陕西 西安 710065)
1 试题呈现
例1如图1,已知直线l1∥l2,直线l3分别与l1,l2交于点A,B.请用尺规作图法,在线段AB上求作一点P,使点P到l1,l2的距离相等(保留作图痕迹,不写作图方法).
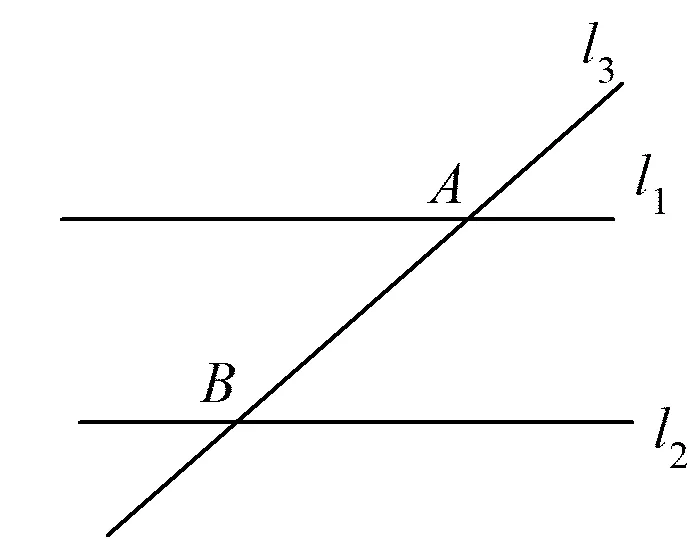
图1
(2021年陕西省数学中考试题第17题)
2 特色解读
2.1 基于课标凸显数学核心素养
《义务教育数学课程标准(2011年版)》(以下简称《课标》)要求学生掌握基本尺规作图和利用基本尺规作图完成综合作图.此题落实了《课标》要求,可用基本尺规作图,也可利用基本作图构造三角形或特殊四边形.学生根据“点P到l1,l2的距离相等”画出草图,发现PA=PB,“执果索因”打开思路,想象并建构相应的几何图形,初步找到作图方法,根据作图过程进行演绎推理.“分析法”和“综合法”指向数学核心素养中的逻辑推理,同时蕴含直观想象素养.
2.2 解法多元呈现上游命题系统
为了得到命题B,寻找命题A,即由命题A可推得命题B,则命题A叫做命题B的上游命题.如果命题A1,A2,A3……都可推得命题B,这就得到了命题B的上游命题系统.
在初中“图形与几何”领域中,什么条件可得到点P为线段AB的中点?关注线段本身,应用线段中垂线的性质;聚焦三角形的相关知识,联想等腰三角形三线合一、直角三角形斜边上的中线等于斜边的一半、全等三角形和相似三角形的性质均可获得点P;聚焦四边形内容,平行四边形对角线互相平分亦可获得点P.
在阅卷中,该题的作图方法精彩纷呈.因为PA=PB这一丰富的上游命题系统让不同能力的学生有不同的切入点,所以在特定的考场环境中,学生会选择自己认知结构中最熟悉、最准确的作图方法.
2.3 编制巧妙贯通初中几何内容
3 解法赏析
笔者参与了中考阅卷,批改此题.学生用尺规确定线段AB的中点的方法丰富多样,以下是答卷中的典型方法.
3.1 线段中垂线的性质
方法1如图2~4所示,作线段AB的垂直平分线.

图2 图3 图4
3.2 三角形相关知识
视角1等腰三角形三线合一.
先作以线段AB为底边的等腰三角形.
方法2如图5,作∠ACB的平分线交AB于点P.
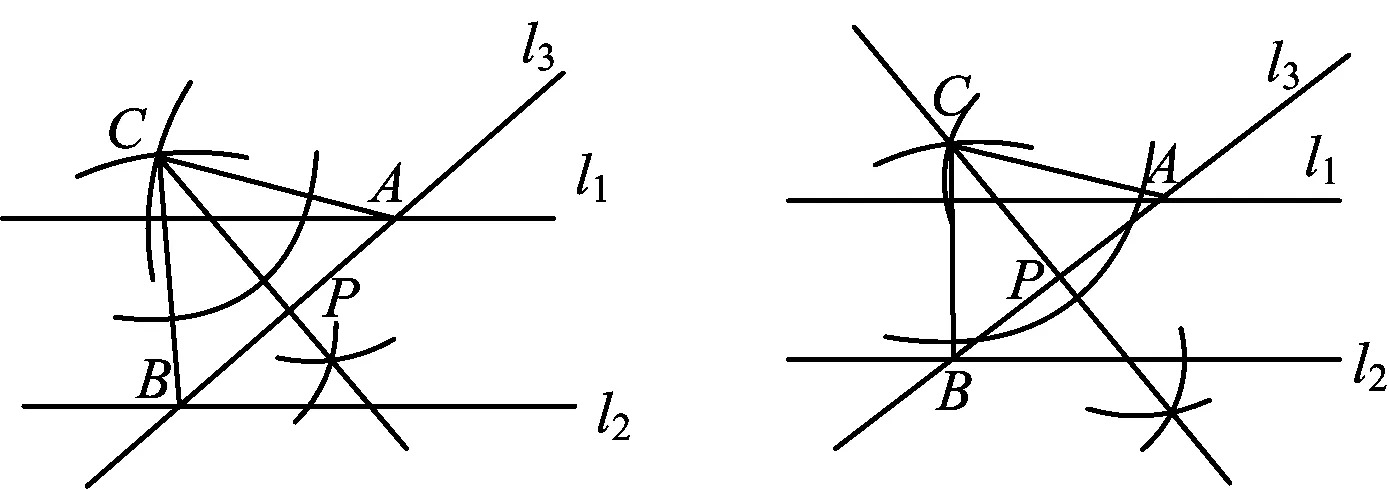
图5 图6
方法3如图6,过点C作直线AB的垂线交AB于点P.
视角2直角三角形斜边上的中线等于斜边的一半.
方法4如图7,作一组同旁内角的角平分线交于点C,再作∠ACP=∠1交l3于点P.
选择焦虑、抑郁及护理满意度作为评价干预效果的情况。焦虑和抑郁分别采用焦虑自评量表(SAS)和抑郁自评量表(SDS)作为调研工具,SAS和SDS均包括20个条目,每个条目采用1至4分4级评分,得分越高表示焦虑或抑郁状况越严重。护理满意度采用本小组自我编译的量表进行评价,该量表包括20个条目,4个维度,每个维度包含5个条目,每个条目采用1至4级评分,得分越高表示护理满意程度越高。经验证,这三个量表在本人群中的信效度都较好。

图7 图8
方法5如图8,过点A作l2的垂线交l2于点C,作∠PCB=∠1交l3于点P.
视角3全等三角形对应边相等.
方法6如图9,分别以点A,B为圆心、相同的半径画弧,分别交l1,l2于点C,D,联结CD交l3于点P.

图9 图10
视角4相似三角形的性质.
方法7如图10,过点A作l2的垂线交l2于点C,作线段AC的中垂线交l3于点P.
方法8如图11,过点A作l2的垂线交l2于点C,作线段BC的中垂线交l3于点P.
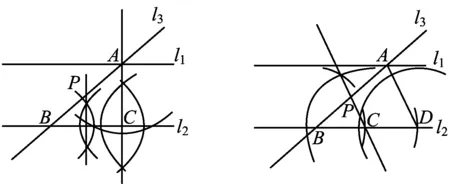
图11 图12
方法9如图12,在l2上依次截取线段BC=CD,联结AD,作∠PCB=∠ADC交l3于点P.
3.3 特殊四边形的性质
视角5矩形的对角线互相平分.
方法10如图13,过点A向l2作垂线交l2于点C,过点B向l1作垂线交l1于点D,联结CD交l3于点P.

图13 图14
方法11如图14,过点A作l2的垂线交l2于点C,以点A为圆心、BC长为半径画弧交l1于点D,联结CD交l3于点P.
方法12如图15,分别作两组同旁内角的角平分线相交于点C,D,联结CD交l3于点P.
视角6菱形的对角线互相平分.
方法13如图16,作∠BAD=∠CAB交l2于点D,作∠ABC=∠ABD交l1于点C,联结CD交l3于点P.
视角7平行四边形的对角线互相平分.
方法14如图17,分别以点A,B为圆心、相同的长为半径在l3的异侧画弧,再分别以点A,B为圆心、相同的长为半径在l3的异侧画弧,相交产生点C,D,联结CD交l3于点P.
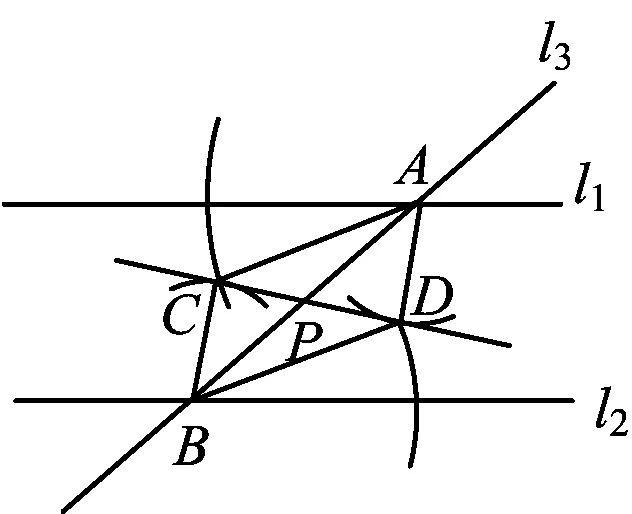
图17
方法15如图18,在直线l1上取一点C,联结BC,作∠BAD=∠CBA交l2于点D,联结CD交l3于点P.
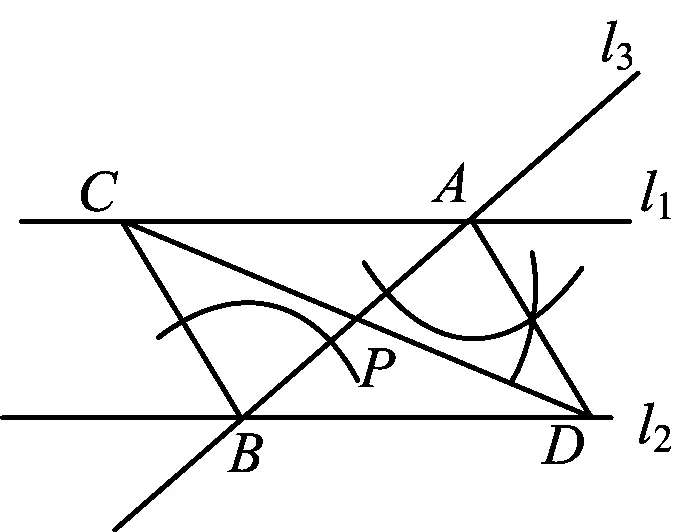
图18
在以上方法中,方法1使用率最高,尺规作线段中垂线的理论依据是等腰三角形的性质,即在l3的异侧或同侧作以AB为底边的两个等腰三角形,产生两个顶角的顶点.若只有一个等腰三角形,能否得到点P?联想等腰三角形的性质产生方法2和方法3.方法6是较为简洁的方法,也可看成ACBD的对角线互相平分.从这个视角来看,关键是构造以AB为对角线的平行四边形,如此获得方法10~15.总之,各方法间有着内在的关联.
4 教学启示
4.1 建立上游命题系统,完善数学认知结构
上游命题系统,一方面,可以帮助学生有效地联想已知和未知之间的关系,从而获得解题思路.例如,该题要求学生储存“获得中点的上游命题”,若拥有相关的上游命题系统,则会获得更优的作图方法.另一方面,建立和使用上游命题系统的过程就是在培养发散思维能力.例如,学习了平行四边形对角线互相平分,可提问“回顾旧知,还有哪些条件可以得到线段中点”,让学生打开已有的数学认知结构搜寻到线段中垂线性质、等腰三角形三线合一性质等来建立上游命题系统.这个过程有利于形成发散性思维,提高有效联想能力,培养思维直觉来克服做题时“想不到”的困难.数学的积累就是将重要的分散的几何知识及时有逻辑地、有序化地纳入自己的认知结构.
4.2 加强尺规作图的过程教学,落实数学核心素养
教师在引导学生掌握基本尺规作图的同时,也要让学生清楚背后的依据,作图方法的灵活性就会提高,如该题可以呈现3种中垂线的作图方法.此外,当面对综合作图时,如何找到作图方法呢?1)画出具备条件和求作图形的示意图;2)用“分析法”和“综合法”剖析示意图中各元素之间的关系,结合图形的性质、判定等,想象出对应的几何图形,最终判断使用哪种基础图形,从而落实直观想象素养,同时“分析法”和“综合法”可提高逻辑思维能力和问题解决能力;3)尺规作出图形;4)对作图方法进行证明:将尺规操作的每一步转化为符号语言和文字语言,来论证合理性,让学生“知其然,知其所以然,何由以知其所以然”.总之,尺规作图加深了学生对定理和命题的理解,提高了“动手动脑”的操作能力,是落实数学核心素养中逻辑推理和直观想象的良好载体,深化了学生对平面几何的认识.

