活用教材:回归有价值的数学思维原点
王 涛
(松阳县第一中学,浙江 松阳 323400)
好的数学问题由命题专家精心命制,具有科学性、示范性、经典性、引导性[1].近年来,高考真题以“无背景,不成题;无思维,不命题;无价值,不入题”为命题指导思想,突出选拔功能,其创新度、考查学生数学思维的深度、考查学生数学解决问题能力的高度陡增.因此,课堂教学要回归价值思维的原点,特别是在新授课上,要更好地揭开数学问题的背景、更准确地揭示数学概念的本质、更深入地揭秘有价值的数学思维,引导学生提出有价值的问题、分析有价值的问题、解决有价值的问题.
1 源于教材,高于教材,数学思维要有深度
数学命题源于教材,但高于教材.对数学概念、数学知识的理解从具体到抽象,又从抽象到更具体,不断地循序渐进.教师要在循序渐进中促进学生的数学思维走向深刻.例如,对抽象函数的考查,其思维的原点在于理解问题的数学抽象表达形式,深刻理解函数的概念和性质.因此,教师在课堂教学中要引导学生回顾、深刻理解函数的概念和性质.
例1(多选题)已知函数f(x)的定义域为R,f(xy)=y2f(x)+x2f(y),则
( )
A.f(0)=0
B.f(1)=0
C.f(x)是偶函数
D.x=0为f(x)的极小值点
(2023年全国数学新高考Ⅰ卷第11题)
分析对于选项A,令x=y=0,得
f(0)=0f(0)+0f(0)=0.
对于选项B,令x=y=1,得
f(1)=1f(1)+1f(1),
则
f(1)=0.
对于选项C,令x=y=-1,得
f(1)=f(-1)+f(-1)=2f(-1),
则
f(-1)=0.
令y=-1,得f(-x)=f(x)+x2f(-1)=f(x),又函数f(x)的定义域为R,故f(x)为偶函数.
对于选项D,不妨令f(x)≡0,即f(x)恒等于0,显然符合题设条件,此时f(x)无极值.故选项D错误.
因此,选A,B,C.
评注思维的原点在于从特殊到一般,如特殊点、特殊元素、特殊位置、特殊函数等,学生思维深刻性在于理解题意.
对于选项D,还可以进行以下分析:
当x2y2≠0时,对f(xy)=y2f(x)+x2f(y)两边同时除以x2y2,得

当x>0时,f(x)=x2lnx,则
令f′(x)<0,得
令f′(x)>0,得
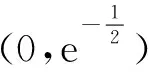
评注在上述分析中,思维的原点在于举反例.在课堂教学中,举反例说明或概念辨析是重要的思想方法之一.
2 依据教材,理解教材,数学思维要有广度
数学命题依据教材、课程标准,教师在理解教材、理解标准、理解学生的基础上,要对数学知识的内在联系进行比较,提高对数学的整体性认识,加深对数学本质的理解.教师在理解数学概念本质的基础上,要拓展数学思维的广度.



(2022年全国数学新高考Ⅰ卷第18题)
本文仅对第1)小题进行分析.

得 sinB=cosAcosB-sinAsinB=cos(A+B)
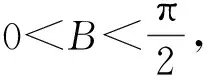

=tanB,

又
故

3 基于教材,拓展教材,数学思维要有适切性
基于教材,充分挖掘知识的内在联系,并进行适度拓展推广,总结形成数学知识、数学方法、数学思想,形成解决问题的有价值的思维逻辑起点[2].
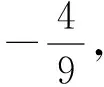
(教材第108页例3)

(教材第121页探究)
例5已知△ABC的两个顶点A,B的坐标分别是(-5,0),(5,0),且AC,BC所在直线的斜率之积等于m(其中m≠0),求顶点C的轨迹.
(教材第146页复习参考题第11题)
通过总结梳理例3~5,可证明以下结论.


还可以引申证明以下2个结论.


评注学生在解决类似的问题之后,就有了更好的解题思路,作为通性通法的新原点.
类比圆、椭圆的斜率之积,还可拓展、推广得到双曲线的类似性质(此处略).
4 读懂教材,讲好教材,数学思维要有效度
读懂教材,讲好教材,对其中蕴含的重要知识技能、思想方法进行必要挖掘与总结提升[3],这些知识方法可能是命题专家的关注点,是数学问题解决的思维原点.教材章节引言中提到“本章我们采用坐标法研究几何图形的性质.坐标法是解析几何中最基本的研究方法”,通过教学总结解析几何题解答的“四步曲”,即“构图→代数化→运算→结论”,其中最关键的是“代数化”思想.

1)求l的斜率;
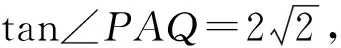
(2022年全国数学新高考Ⅰ卷第21题)
分析将核心条件代数化,令点P(x1,y1),Q(x2,y2),得
kAP+kAQ=0,
即
将问题目标代数化,得

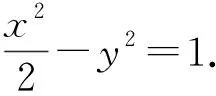
(1-2k2)x2-4mkx-2m2-2=0,
因此
由Δ=16m2k2-4(2m2+2)(2k2-1)>0,得
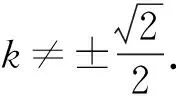
又kAP+kAQ=0,得
即 (x1-2)(kx2+m-1)+(x2-2)(kx1+m-1)=0,
亦即 2kx1x2+(m-1-2k)(x1+x2)-4(m-1)=0,

化简得
8k2+4k-4+4m(k+1)=0,
即
(k+1)(2k-1+m)=0,
得k=-1或m=1-2k.当m=1-2k时,直线l:y=kx+m=k(x-2)+1过点A(2,1),舍去.故k=-1.
解法2设直线l的方程为p(x-2)+q(y-1)=1.

(x-2+2)2-2(y-1+1)2=2,
从而
(x-2)2+4(x-2)-2(y-1)2-4(y-1)=0,
即 (x-2)2+4(x-2)[p(x-2)+q(y-1)]-2(y-1)2
-4(y-1)[p(x-2)+q(y-1)]=0,
亦即 (2+4q)(y-1)2+(4p-4q)(y-1)(x-2)
-(1+4p)(x-2)2=0,

从而
于是
p=q,
故
评注此题凸显了直观想象、逻辑推理和数学运算核心素养.遇到复杂问题时,首先通过可视化思维,借助图形将信息变得有序直观;然后借助流程思维,将问题分为多个流程,再对每个流程进行优化,从而提升思维效度.
好的数学问题能有效引导课堂教学,严格依据《普通高中数学课程标准(2017年版)》(以下简称《课标》),确保“内容不超范围,深度不超要求”,在《课标》范围之内,遵循教育规律,进一步深化基础知识;深刻领会“突出数学概念的本质,重视理性思维的能力,凸显问题解决的能力,坚持核心素养的导向”,强化对基础知识全面深刻的理解和融会贯通的运用,引导学生学有所思、思有所疑、疑有所问、问有所悟;在深刻理解的基础上融会贯通、灵活运用,教师要把教学重点从总结解题技巧转向培养学生的关键能力和学科素养.

