探三步纠错 促深度反思——由两道二元最值试题的错解反思问题设计

吴景峰

(1.北京师范大学未来教育学院, 广东 珠海 519087;2.广州市艺术中学,广东 广州 510060)

0 引言

在一次教师线上研讨中,一位教师发布了一道试题(含正确结果),征求大家的解法.群内的一位教师给出了自己的解法,试题和解法分别如下.

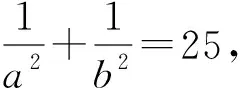
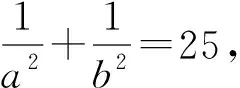
(1)

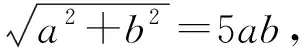
(2)

(3)

(4)

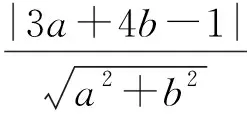
此解法发布后引起了群内议论,虽答案正确,但过程并不正确.在研讨中,时常有教师奔着答案去写过程,就出现答案正确而过程有误的错解.回顾多年来“不等式”单元的教学,无论哪一届学生,无论是使用旧教材还是新教材,类似错解一直广为流传.在学生的作业中,经典的错解还有以下一例.

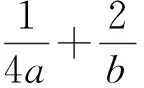
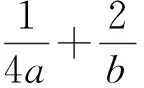
针对上述错解,教师要及时调整教学,引导学生进行错后反思,并反思自身教学中存在的问题,同时开展持续性评价,引导学生用发展的眼光看待错误[1].笔者针对纠错教学,总结了3步纠错,即师生共同完成“为何有错、如何纠错、如何改进”的深度反思.

1 为何有错

通过上述2道试题的错解,可知在“不等式”单元学习中,求最值问题时有3个常见误区:1)误认为二元最值问题,就一定用到基本不等式;2)误认为运用基本不等式,就一定能求最值;3)误认为运用基本不等式得到定值,就一定是最值.教师应指出误区中的表现形式,及时引导学生去深挖背后的原因.

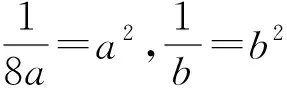
2 如何纠错

2.1 例1的分析

关于错解,式(1)～(3)都属于正确步骤,难点在于式(3)的后续处理.首先,分析式(3)的结构,用配凑法处理,进一步观察,从代数角度寻求突破;其次,可分析问题结构,联想其几何意义,从几何角度求解;最后,分析条件结构,采用三角换元,从函数角度求解.通过一题多解,多角度训练和提高学生的基本技能.

正解1(代数角度)

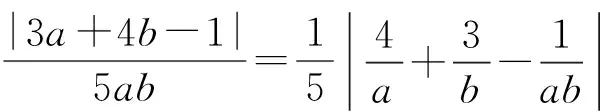
联想条件可得

即

正解2(几何角度)

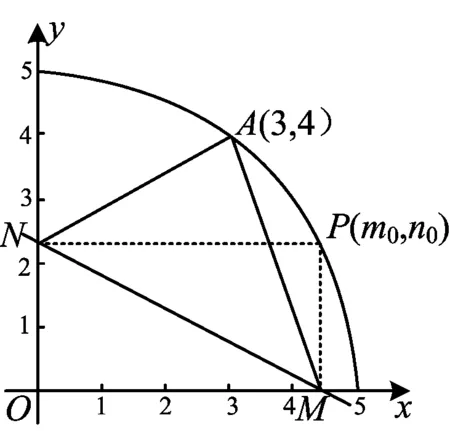
图1

正解3(函数角度)

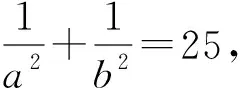
后面步骤与正解1类似,可得

(5sinα-3)(4-5cosα)≥0,

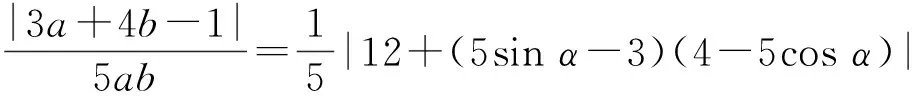
2.2 例2的分析

例2的错解2使用了配凑法,利用基本不等式得出定值,但由于取等条件无解,可尝试引入参数λ进行配凑,即“+λ(a2+b2)-λ”,在取等条件处解出λ.还可以尝试换元法,转化为函数求最值问题.

正解1(代数角度)

当且仅当

正解2(函数角度)

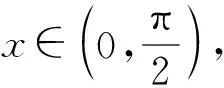
评注正解1是引入参数的配凑法,属于基本技能的提升;正解2是三角换元,利用导数工具处理三角函数最值.这2种方法均是最值问题中的通性通法.

例1和例2还可尝试利用a表示b代入目标式,直接构造函数求最值,但函数结构复杂,运算量较大.

3 有何改进

在纠错教学中,除了让学生纠正,更需要让学生深刻理解错因,在理解的基础上提升能力.教师可先从学生普遍出现的错解中反思自身的教学问题.

3.1 问题串的改进

在教学时,对基本不等式的“一正、二定、三相等”虽朗朗上口,但若缺乏引导学生对其背后原理的理解,则会沦为形式,是不可取的.教师通过合理的问题串设计,引发学生的认知冲突,引发学生的深度反思,让学生认清错误表现形式背后的根源,从而更好地领悟正解的妙处.

问题1基本不等式成立的条件是什么?

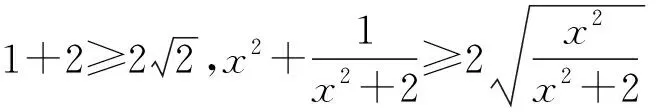
追问1-2f(x)≥0的含义是什么?

追问1-3f(x)≥0是否包含了最值的含义?

追问1-4f(x)≥0还要补充什么条件才包含最值的含义?

设计意图总结出任意两个正数均可使用基本不等式,并强调“≥常数”的含义是“不小于该常数”,在此基础上必须存在x使等号成立才包含最值含义.

问题2使用基本不等式求最值的条件是什么?

追问2-1回顾“一正、二定、三相等”的含义,如何理解这里的“定、等”?

设计意图把问题1与问题2区分开,是有必要的,在于引导学生归纳出“正”是基本不等式成立的条件,结合追问1-4可得“定、等”是最值的要求.

追问2-2“定、等”会出现在哪些步骤?而例1的错解、例2的错解1中的“定”出现了吗?例2的错解2中的“等”出现了吗?

设计意图启发学生发现,例1的错解和例2的错解1中的“定”没有出现,而通过“等”得到的解代入求得的不是“定”;例2的错解2中没有出现“等”,而“等”所求结果与已知矛盾,于是最值不可取.

追问2-3同学们能自编一个问题,说清楚“定、等”应如何体现吗?

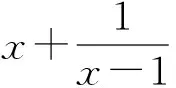
追问2-4若正实数a,b,满足ab=a+b+3,求ab的取值范围.“定、等”体现在哪?

(人教A版《普通高中教科书·数学》(必修第一册)第58页第5题)

⟺ab≥9(定值),

当且仅当

即a=3,b=3时,等号成立.足以说明9为最小值.

问题3利用基本不等式证明不等式时,有必要说明取等条件吗?

设计意图证明不等式,并不是求最值,不能与问题2混淆,因此不需要说明取等条件,只需要说明“正”即可使基本不等式成立.

问题4从逻辑上分析,利用基本不等式时,为何会出现回代取等条件的错误?如何认识这种表现形式的错误?

追问4-2如何认识例1错解中的错?例2错解1中的错呢?

设计意图回归错解进行反思,深刻认识错因.当3a=4b时,

当3a≠4b时,

这两点在逻辑上不足以说明最值,也不符合最值的条件.例2的错解1是同样的道理.不同的是,例1的错解碰巧得到了正确答案,而例2的错解1没有得到正确答案.

追问4-3能举出函数的相关例子,利用函数图象,多角度解释类似的表现形式?

追问4-4通过例2错解2的错,同学们有什么启发?

设计意图让学生认识到,无论单次还是多次使用基本不等式,除了要有“定”,还要注意“等”.

上述问题串的4个核心问题,既可在高一学生初学基本不等式时复习引入,也可以在高三的一轮复习中引入,让学生更好地理解基本不等式求最值的条件.

3.2 变式训练的改进

为了让学生更好地掌握求最值的一些基本技能,教师可以在例1和例2的基础上进行变式训练,通过变式训练的一题多解,全方位拓宽思路,提升能力.

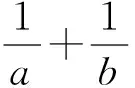
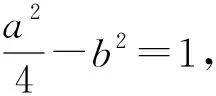
上述5道变式题解法很多,留给读者自行探究,教师可根据学情进行选择,由浅入深,在理解的基础上逐步提升学生解决问题的能力.

4 结束语

唯有引导学生区分最值与不等式的含义,真正领会利用基本不等式求最值的条件,“一正、二定、三相等”的口诀才能体现数学的自然与简洁.一方面,教师通过寻找错因、分析错因和纠正错解,渗透通性通法思想,提升学生的技能和素养;另一方面,教师通过改进问题设计和变式训练,发展自身的专业素养,师生共同完成“为何有错、如何纠错、如何改进”的深度反思.