数学综合实践类试题的命制策略
张娟萍
(杭州市青云初级中学,浙江 杭州 311399)
“综合与实践”是初中数学4个课程领域之一.重在解决生活实际问题和跨学科问题,常采用项目式学习[1].“综合与实践”活动包含“任务”“综合”“实践”这3个要素.其中设计“任务”是关键,挑战性的任务能启发学生进行思考和开展数学活动.“综合性”体现在解决实际生活问题或者跨学科的问题,发挥数学的学科价值,提高四能,发展应用意识、创新意识和实践能力.“实践”主要包含“数学探究”和“数学建模或数学实际应用”,是指综合运用所学的数学思想、方法、知识、技能解决数学、生活和社会的问题[2].“综合与实践”活动能够落实核心素养,发展学生的高阶思维能力.
在数学教学中,能够较好地落实综合实践的关键在于综合实践在评价中的体现.当前,国内纸笔测试作为课程达标以及高一级学校选拔的依据,在教育中的地位和导向不言而喻.2023年7月26日,浙江省教育厅发布《浙江省教育厅关于实施初中学业水平考试全省统一命题的通知(征求意见稿)》,引导教师积极探索基于情境、问题导向、深度思维、高度参与的教学模式;注重命题考查思维过程、创新意识和分析问题、解决问题的能力;强调提高探究性、开放性、综合性试题的比例,积极探索跨学科命题.
纸笔测试与学科内容、学生的关联在于提供考查任务的材料,相比于“成品”的学习,学生高阶思维和核心素养是在“创生”的过程中发展起来的,“复杂情境”的问题解决是引发学生“创生”的载体.引发学生复杂思考、产生高阶思维的前提就是要有挑战性任务.《义务教育数学课程标准(2022年版)》(以下简称《课标》)对学业水平测试的试题命制,要求创设合理情境,结合学生认知水平和生活经验,设计合理的生活情境、数学情境、科学情境[3].下面笔者以近3年7~9年级的期末测试命题为例,谈谈如何采用生活实际问题和跨学科问题的情境作为命题材料来突破对“综合与实践”的考查.
1 由生活情境设置命题材料
调查发现,学生在面对真实情境的数学问题时解题表现较差.例如,2020年和2021年区域九年级期末命题中都考查了黄金分割的知识,试卷难度系数同为0.75.
例1图1是一个包装盒的俯视图,线段AB是这个俯视图的中轴线.某公司想在中轴线AB上找到靠近点A的一个黄金分割点E做装饰.已知AB=2.8分米,求点E到点A的距离.

图1
(2020年浙江省杭州市上城区初三数学一模试题第21题)
例2苏堤南起南屏山麓,北到栖霞岭下,全长2.8公里.苏堤上有名的六吊桥由南到北分别是映波桥、锁澜桥、望山桥、压堤桥、东浦桥、跨虹桥.压堤桥约居苏堤南北的黄金分割位,旧时又是湖船东来西去的水道通行.从地图上看,压堤桥位于苏堤北部,请你结合上述描述,估计压堤桥到栖霞岭下的大致距离.
(2021年浙江省杭州市上城区初三数学期末试题第8题)
2020年和2021年该题的得分率分别是0.89和0.64,可以发现:用实际生活背景引入,相较于纯知识应用的考查,学生的得分率下降28%.这说明许多学生缺少在真实背景中提炼出数学问题的能力.
1.1 设计贴合学生的实际生活情境
实际生活情境让学生有机会结合现实经验理解题目隐含的信息.
例3小华的U盘容量为8 GB(1 GB=1 024 MB),U盘中已经存储了1个视频文件,其余空间都用来存储照片.若每张照片占用的内存容量均相同,照片数量x(张)和剩余可用空间y(MB)的部分关系如表1所示:
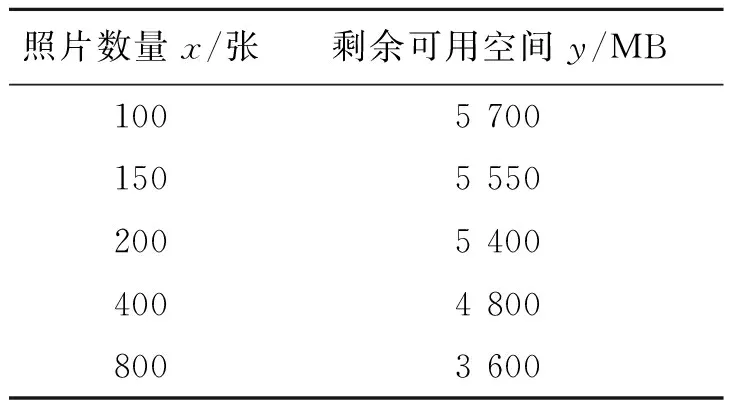
表1 照片数量与剩余可用空间之间的关系
1)求出y与x之间的关系式;
2)若U盘中已经存入1 000张照片,那最多还能存入多少张照片?
(2019年浙江省杭州市上城区初三数学一模试题第20题)
分析对于第1)小题,学生根据生活经验,得到数量关系为:剩余可用空间y(MB)=总容量-存照片要用的空间-已经存储视频占用的空间.设视频文件占用的内存容量为b(MB),每张照片占用内存容量为k(MB),可得
y=8×1 024-kx-b,
用待定系数法可以得到解析式.
第2)小题其实是实际问题中求函数值的知识.
此题也可以用拟合函数的方法,通过描点,说明数据分布在一条直线的附近,近似表示为一次函数y=kx+b,利用数据中的信息,求得k,b的值,得到x和y的关系.然后把其他的数据代入去验证是否都符合这个一次函数.
1.2 用数学建模解决实际问题
国际上常把中小学数学课程中的数学建模看作一种特殊的数学应用活动,学生通过构建新的数学模型去解决实际问题.这些都可以培养学生的应用意识和模型观念,是《课标》强调的数学核心素养的重要表现形式.
一次函数可以表示2个变量之间的各种线性关系,其中包括匀速直线运动的数学模型、弹簧拉伸长度的数学模型等.反比例函数是反映2个乘积为定值的变量的变化规律,常常会涉及面积的数学模型.解决实际背景问题是学生将某种现实情境“数学化”的过程.
例4已知视力表上视力值V和字母E的宽度a(mm)之间的关系是我们已经学过的一类函数模型,字母E的宽度a如图2所示.经整理,视力表上部分视力值V和字母E的宽度a(mm)的对应数据如表2所示:
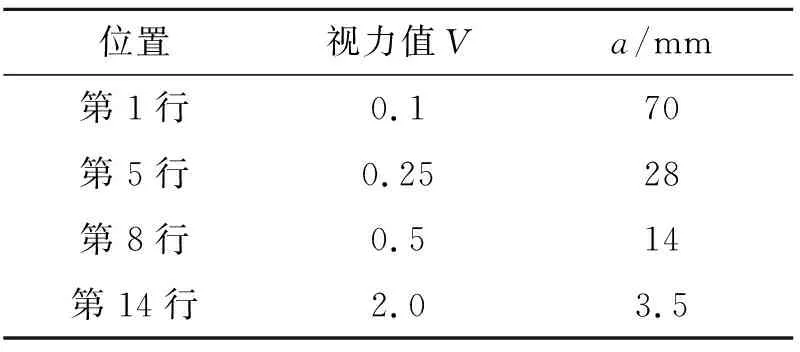
表2 部分视力值V和字母E的宽度a的对应关系

图2
请你根据表2中的数据判断并求出视力值V与字母E宽度a(mm)之间的函数表达式.经过测量,第4行和第7行首个字母E的宽度a(mm)的值分别是35 mm和17.5 mm,求第4行、第7行的视力值.
(2023年浙江省杭州市临安区初二数学期末试题第20题)

1.3 在生活实际背景中体验概率统计
统计与概率的广泛应用性为联系生活实际提供了可行性,学生只有通过参与实践活动才能体会统计与概率知识的真实性和必要性,感悟概率统计与生活的密切联系,进一步体会“数学来源于生活,服务于生活”.
例52023年1月17日国家统计局发布了近5年我国人口、出生人口数量,数据统计如表3所示:
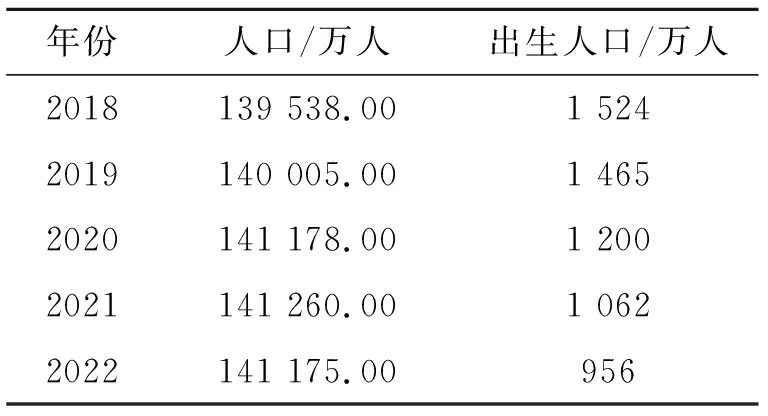
表3 近5年我国人口、出生人口数量统计表
某同学认为,从统计数据来看,人口数量都是逐年增加的.你认为他说的对吗?新生婴儿出生的男女比例约为2∶1.6,预计2025年出生人口为819万人,请估计2025年出生人口中男孩的人数.
(2023年浙江省杭州市临安区初三数学一模试题第18题)
评注此题根据数据做一些简单运算,就可以推导得到结论,通过数学问题情境让学生了解和关注社会状况.数学与实际生活问题的关联体现在:将生活原型抽象成数学模型;将数学模型解读成生活原型;由生活原型到数学模型再回到生活原型.
2 用跨学科的材料命制数学考题
《课标》中所涉及的跨学科主题学习是育人方式变革的有效载体,也是未来教育发展的意义所在.跨学科的真实情境,通常也是复杂陌生的、具有一定挑战性的情境,学生几乎不可能仅运用数学知识解决问题,还需要调用多学科的知识技能、收集新信息、开拓学习新方法.
2.1 建立数学知识与其他学科知识之间的联系
1)力的分解.
例6一个长方体木箱沿斜面下滑,当木箱滑到如图3所示位置时,AB=2,木箱高BD=1,斜面坡角为30°.求木箱顶点D距AC的高度.
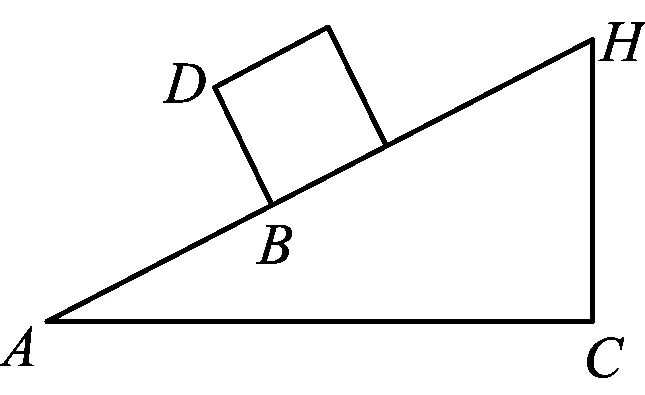
图3
(2019年浙江省杭州市上城区数学初三期末试题第19题)
评注力的分解基本如图4所示,力的分解中最关键的是将重力分解成垂直斜面的力与斜面的支撑力形成一对平衡力.重力分解成平行斜面的力与摩擦力形成一对平衡力,从而木箱沿斜面匀速下滑.这里△DBE,△AEF,△ACH构成相似三角形.
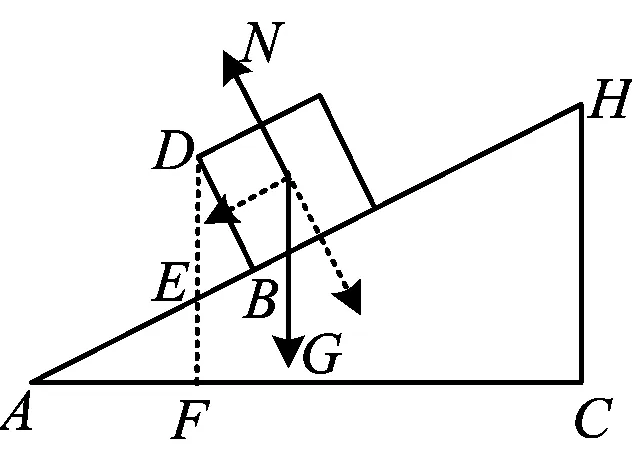
图4
2)光的反射.
例7光线反射是一种常见的物理现象,在生活中有着广泛的应用.例如,提词器可以帮助演讲者在看演讲词的同时也能面对摄像机,自行车尾部的反光镜就是应用了光的反射原理.
提词器的原理如图5所示,AB表示平面镜,CP表示入射光线,PD表示反射光线,∠CPD=90°,求∠APC的度数.自行车尾部的反光镜在车灯照射下,能把光线按原来的方向返回(如图6),a表示入射光线,b表示反射光线,a∥b.平面镜AB与BC的夹角∠ABC=α,求α;如图7,若α=108°,设平面镜CD与BC的夹角∠BCD=β(其中90°<β<180°),入射光线a与平面镜AB的夹角为γ(其中0°<γ<90°),已知入射光线a从平面镜AB开始反射,经过2~3次反射,当反射光线b与入射光线a平行时,请直接写出β的度数(可用含γ的代数式表示).

图5 图6 图7
(2021年浙江省杭州市上城区数学初一期末试题第23题)
评注光的反射原理用到数学的轴对称、平行线知识.此题进一步促进学生理解数学中轴对称与平行之间的转化.其本质是位置关系的变换,涉及变换、分类讨论等数学思想.
2.2 构建学科背景的数学模型
运动学中的刹车问题反映了直线运动的函数模型.
2.2.1 构建一次函数的匀速直线运动模型

1)求5秒加速期的平均速度;
2)设匀加速直线运动的路程为s,求s关于t的函数表达式.
(2021年浙江省杭州市上城区数学初三期末试题第20题)
2.2.2 构建二次函数匀变速直线运动模型
例9已知汽车刹车后行驶的距离s关于行驶的时间t的函数解析式是s=15t-6t2,汽车刹车后到停下来滑行了多少米?
(2023年浙江省杭州市八县区(包含临安区)数学初三开学检测试题第15题)
评注学生对二次函数抛物线图象的形象理解通常是自由落体运动、抛球运动,因此理解水平直线上刹车运动距离的最大值是刹车后移动距离,有许多困难.因此,在例9的测试(得分率为0.36)并讲评后,过2个月的时间,再检测学生“刹车后移动距离”的问题(得分率0.38),学生问题解决的能力没有明显增加.这说明:1)物理背景的介入对学生的理解有很大影响;2)学生没有厘清二次函数的本质是反映匀变速直线运动的函数模型;3)学生没有理解“为什么用最大值来解释刹车距离”.
解决跨学科的实际问题,包含5个步骤:审题—翻译—关联—建模解模—回译.
将数学模型运用于跨学科情境时要经过形式化等抽象过程,感悟数学的广泛应用性及数学模型的简洁性.事实上,大多数数学模型都依赖于所描述问题的学科背景.例如,生物学中的种群增长模型、气象学中的大气环流模型、经济学中的组合投资模型、社会学中的人口发展模型等.因此,通过跨学科的建模活动,可以使学生体会到数学模型作为一种普适性的语言在其他学科中的实际作用.
3 用项目学习的材料命制试题
项目学习活动流程如下:根据任务提出问题、并聚焦问题—规划方案—开展数学活动—探究过程—成果分析分享—表现性评估跟进.
例如,“地球有多大”的探索活动.浙教版《义务教育教科书·数学》(七年级下册)第20页阅读材料“地球有多大”,学生一般以项目式学习探究相关内容,因此在某区命题如下:地球有多大?2 000多年前,古希腊数学家埃拉托斯特尼利用太阳光线测量出了地球子午线的周长.下面让我们一起开启“探求地球周长”的数学项目化学习之旅.
项目任务1如图8,某日正午,小红在B地(与太阳直射点A在同一子午线上)测得太阳光与木棍的夹角为ɑ,则∠AOB=______.若测得AB之间弧长为l,则地球子午线周长为______(用含ɑ,l的代数式表示).
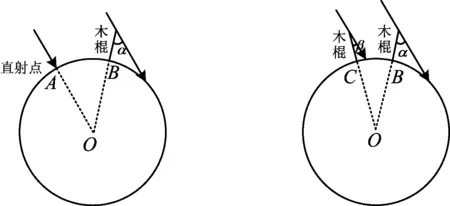
图8 图9
项目任务2如图9,某日正午,小红和小明在同一子午线的B地、C地测得太阳光与木棍的夹角分别为ɑ,β,则∠BOC=______.若测得BC之间弧长为l,则地球子午线周长为______(用含ɑ,l的代数式表示).
项目任务3如图10,日落时,身高为h的小亮趴在地上平视远方,在太阳完全从地平线上消失的一瞬间,按下秒表开始计时.同时马上站起来,当太阳再次完全消失在地平线的瞬间,停止计时.小亮利用这个时间差和地球自转的速度计算出了∠PQH=θ,请据此计算出地球的半径与周长(用含h,θ的代数式表示).
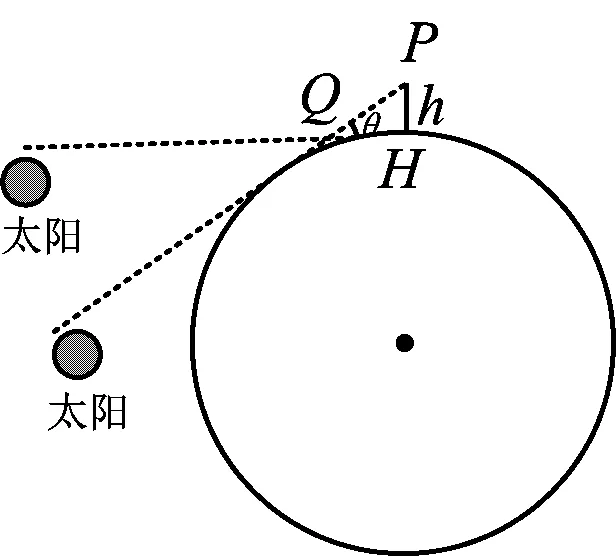
图10
(2023年浙江省嘉兴市嘉善县初中教育质量调研试题第22题)
当情境对学生有强烈的吸引力时,能激发学生对于问题解决的内在需要,有效地推进思维过程.相反地,过于理想化、模式化的“伪情境”会由于信息的确定性过高致使学习者无法产生认知冲突.《课标》非常重视在真实情境,尤其是综合与实践、项目式学习,以及跨学科的情境,让学生从数学角度观察与分析、思考与表达、解决与阐释社会生活以及科学技术中遇到的现实问题,感受数学与科学、技术、经济、金融、地理、艺术等学科领域的融合,刺激学生产生多样化的思考,发展学生综合核心素养.学生在面对日常生活和其他学科时,能够从数学的角度来考查,观察其中蕴含的数学概念、性质与关系,并运用数学思想方法,将实际问题表征为数学问题,再运用数学方法加以解决.用数学的知识、探究方法、思维方式解决问题,实现跨场域、跨时段、跨学科联通.

