基于几何直观,聚焦图形结构的“代数表达”——2023年杭州市数学中考第23题的解析与思考

蒋玲玲

(杭州市富阳区永兴学校初中部,浙江 杭州 311400)

《义务教育数学课程标准(2022年版)》指出,几何直观主要是指运用图表描述和分析问题的意识与习惯,根据语言描述画出相应的图形,分析其性质,建立数与形的联系,明晰问题解决的思维路径[1].“代数表达”是对平面几何的直观图形和图形变化的定量刻画,通过对角度、长度的度量以及位置关系的定量分析[2],以特定的代数形式进行表达.在初中平面几何问题中,“图形结构”如何进行“代数表达”,“代数表达”又在刻画什么样的“图形结构”,这是学生的难点,使其无法理解问题的本质.几何直观能为学生建立“图形结构”和“代数表达”的桥梁,分析图形结构的元素与性质,为其代数表达指明方向,启发问题解决的思路.笔者以2023年浙江省杭州市数学中考第23题为例进行剖析与思考.

1 试题呈现

例1如图1,在⊙O中,直径AB垂直弦CD于点E,联结AC,AD,BC,作CF⊥AD于点F,交线段OB于点G(不与点O,B重合),联结OF.

图1

1)若BE=1,求GE的长;

2)求证:BC2=BG·BO;

3)若FO=FG,猜想∠CAD的度数,并证明你的结论.

(2023年浙江省杭州市数学中考试题第23题)

分析作为2023年浙江省杭州市数学中考试卷的最后一题,整个图形结构可以说“中规中矩”,简洁明了,对其进行定性分析,可得以下基本结论:

1)整个图形由弦CD的位置决定,可由弦CD的长度或∠CAD的大小刻画;

2)整个图形结构是轴对称的,局部图形结构有等腰△ACD,Rt△ACF,以及“双垂形”“八字形”下的直角三角形相似,有Rt△CDF∽Rt△CGE∽Rt△AGF∽Rt△ABC∽Rt△ACE∽Rt△CBE;

3)点G是△ACD的垂心.

2 解法探究

2.1 观察元素关系,识别“代数表达”下的本质结构

第1)小题的“代数表达”是“BE=1”,刻画的是线段BE的长度.观察线段BE和GE,容易猜想GE=BE=1,形成解题思路,主要有以下两种解法.

1)解法1由题意可得∠CEG=∠CEB=90°,∠BCD=∠BAD.因为CF⊥AD,AB⊥CD,所以

∠DAE=∠DCG, ∠BCE=∠ECG,

从而

△CEG≌△CEB,

于是

GE=BE=1.

解法2由题意可得∠ADC=∠ABC,∠AGF=∠CGE.因为CF⊥AD,AB⊥CD,所以

∠AGF=∠ADC, ∠CGE=∠CBA,

从而△CBG为等腰三角形,于是

CG=CB,CE⊥BG,

故

GE=BE=1.

评注解法1通过证明△CEG≌△CEB,得GE=BE=1;解法2通过证明△CBG为等腰三角形,得GE=BE=1.前者只观察到两条线段本身的数量关系,得到的图形结构是△CEG≌△CEB;后者还观察到了它们与线段CD的位置关系,从而识别出更为一般的轴对称的等腰三角形结构.解法2不仅建立了局部图形结构和整体图形结构的联系,还可以进一步发现“三角形的垂心关于边的对称点在其外接圆上”的结论.重点观察元素与元素之间的数量与位置关系,能让“代数表达”更有方向性,揭示图形的本质结构.

2.2 结合图形性质,联想“代数表达”下的相关结构

第2)小题的“代数表达”是“BC2=BG·BO”,刻画的是线段长度乘积的数量关系.分析图形的性质,形成解题思路,主要有以下3种证法.

2)证法1如图2,联结OC,则∠OCB=∠GBC.由第1)小题得∠CGB=∠OBC,则

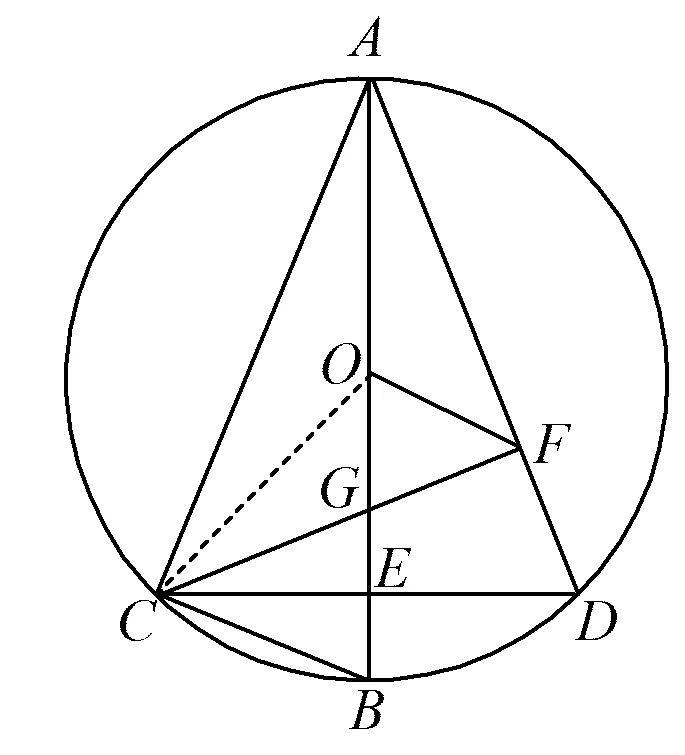
图2

△CBG∽△OBC,

从而

即

BC2=BG·BO.

证法2由AB是直径,AB⊥CD,可得

∠ACB=∠CEB=∠CEA=90°,

从而

∠BCE+∠CBA=90°,

∠CBA+∠CAB=90°,

即

∠BCE=∠CAB,

于是

△BCE∽△BAC,

进而

即

BC2=BE·AB.

因为

AB=2OB,BG=2BE,

所以

证法3如图2,联结OC,可得

BC2=CE2+BE2=OC2-OE2+BE2

=(2OB-BE)·BE+BE2

评注证法1是由线段长度的乘积,结合“相似三角形对应边成比例”的性质,联想到证明△CBG∽△OBC来解题;证法2是由比例中项BC,结合射影定理,联想到证明“双垂型”的相似三角形来解题;证法3则是由线段“平方”,结合勾股定理,联想到直角三角形边长关系来解题.3种证法的出发点不同,所结合的图形性质不同,从而联想到的图形结构也不同.大多数学生选择证法1或证法2进行解题,建立了“线段成比例”与“相似三角形对应边成比例”的直接联系,而证法3则需要对两个直角三角形的边长关系有清晰的认识.充分理解图形性质的“代数表达”并能联想到对应的图形结构,使同一个“代数表达”能刻画出多种相关的图形结构,从而更好地了解多个局部图形结构的相互关系.

2.3 构造直观图形,刻画“代数表达”下的同一结构

第3)小题的“代数表达”是“FO=FG”,刻画的是两条线段长度的等量关系.观察图形,由于CF⊥AD,通过合情推理,猜测∠CAD为特殊角,容易猜想∠CAD=45°,形成解题思路,即证明△ACF为等腰直角三角形.

方法1构造全等图形,证明AF=CF.

3)解法1猜想∠CAD=45°,如图2,联结OC.设∠DAB=α,则

∠AGF=90°-α,

由FO=FG,得

∠GOF=∠OGF=90°-α,

故

∠AOF=90°+α.

又

∠COB=2∠CAB=2α,

知

∠COF=90°-α+2α=90°+α=∠AOF.

因为

AO=CO,OF=OF,

所以

△AOF≌△COF,

从而

AF=CF,

且

CF⊥AD,

故

∠CAD=45°.

解法2猜想∠CAD=45°,如图3,延长FO交AC于点H.由FO=FG,可得

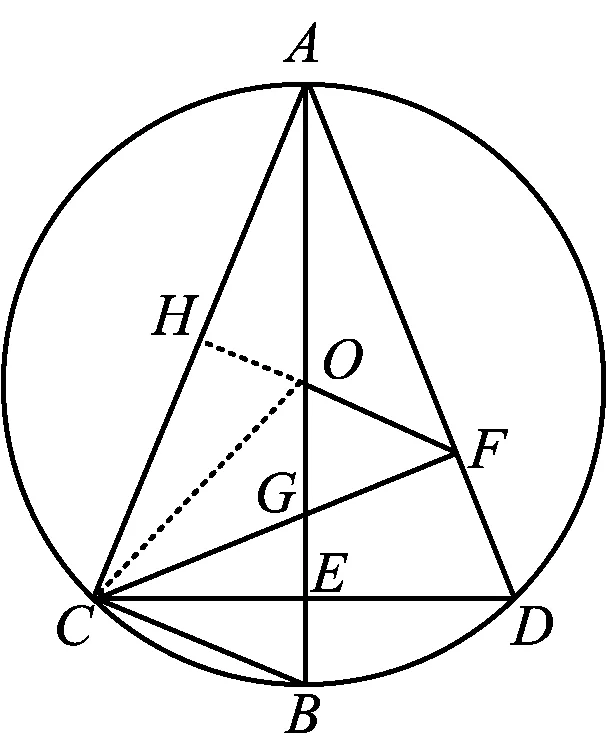
图3

∠GOF=∠OGF=∠CGB

=∠CBG,

从而

OF∥CB.

由CB⊥AC,知

FH⊥AC.

因为FH过圆心O,所以

AH=CH,

故FH垂直平分AC,可得

AF=FC.

又由

CF⊥AD,

可得

∠CAD=45°.

分析解法1是通过构造△AOF≌△COF来证明,解法2是通过构造垂直平分线,实质是构造了△AHF≌△CHF来证明.二者都将目标转化为证明AF=CF,用“边”的“代数表达”来刻画等腰Rt△ACF的“图形结构”.

方法2构造等腰直角三角形,证得∠CAD=45°.

解法3猜想∠CAD=45°,如图4,延长CF交⊙O于点H,联结AH,OH.由∠AGH=∠CGB,∠CBG=∠AHG,可得

图4 图5

△AGH∽△CBG.

由题意可证

△AGF≌△AHF,

故

GF=OF=FH,

从而

OH⊥AB,

于是

由于

CF⊥AD,

故

∠CAD=45°.

解法4猜想∠CAD=45°,如图5,延长CF交⊙O于点H,联结AH,OH,作点F关于AB的对称点M,联结GM并延长交⊙O于点N,联结AN,NO.由对称性可知△AGH≌△AGN,与解法3相同,证得OH⊥AB,由对称性易证NO⊥AB,故点N,O,H共线,可得∠NAH=90°.设∠DAB=α,得

∠CAB=∠DAB=∠HAD=∠CAN=α,

因此

∠CAD=2α=45°.

解法5猜想∠CAD=45°,如图6,联结CO.设∠DAB=α,由题意得∠COB=2α,且

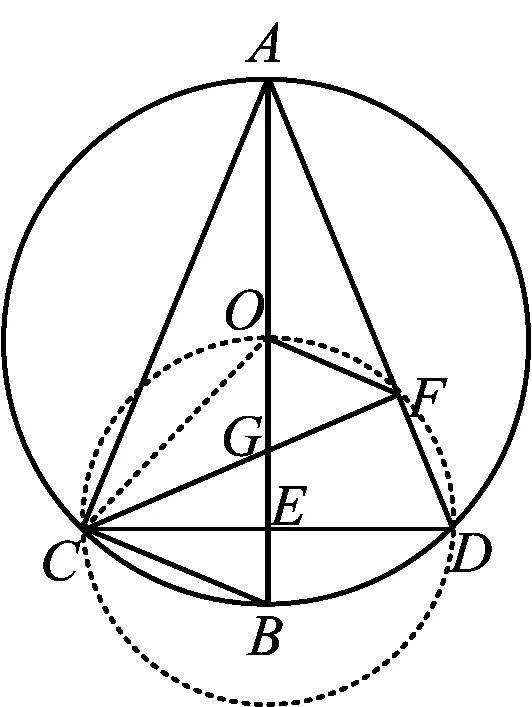
图6

∠GOF=∠OGF=∠ADC=90°-α,

从而 ∠COF+∠FDC

=2α+90°-α+90°-α=180°,

因此点C,O,F,D共圆.由CF⊥FD,可得CD为直径,E为圆心.因为OE⊥CD,OE=CE,所以

∠COE=45°,

故

∠CAD=∠COE=45°.

评注解法3根据“三角形的垂心关于边的对称点在其外接圆上”,构造等腰△AGF,结合条件构造出等腰Rt△AOH来证明;解法4则是在解法3的基础上,通过整体对称,先构造轴对称图形,进而构造Rt△ANH来证明;解法5是将“角”的条件聚焦到四边形COFD中,通过“导角”证得点C,O,F,D共圆,从而构造出等腰Rt△AOE来证明.3种解法都是通过构造新的等腰直角三角形,用“角”的“代数表达”来刻画等腰Rt△ACF的“图形结构”.

这两种思路都是基于几何直观,观察和猜想得到直观图形结构,分析线段、角之间的关系,结合特殊三角形的性质、圆的轴对称性,构造直观图形,用多种“代数表达”来刻画同一个“图形结构”,拓宽了问题解决的思路,加深了对图形结构本身的代数理解.

3 拓展应用

作为2023年浙江省杭州市数学中考试卷的最后一题,从问题解决来看,第1)小题和第2)小题都在研究一般情况下整个图形的“代数表达”下的局部“图形结构”;第3)小题刻画的则是特殊情况下的特殊图形结构.整个“图形结构”的位置用角的大小或者线段之间的关系进行“代数表达”,为设计变式提供了思路.

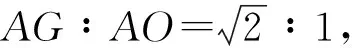
图7

分析变式1对例1第3)小题的条件进行了修改.例1中用OF和EF的数量关系进行代数刻画.通过对轴对称后的整个图形结构研究,可以得到特殊位置下所有线段的数量关系,聚焦到圆的结构和等腰△ACD的元素,用半径AO和线段AG的数量关系进行代数刻画,如图8所示.变式1的解决可参考例1第3)小题的解法3和解法4.

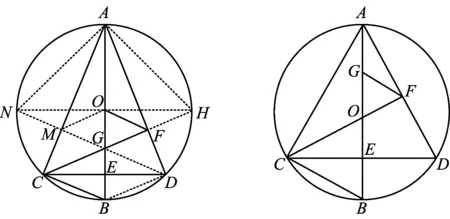
图8 图9

变式2如图9,在⊙O中,直径AB垂直弦CD于点E,联结AC,AD,BC,联结CO并延长交AD于点F,取AO中点G,联结GF,得到GF=OF且GF∥BC.猜想CF与AD的关系,并证明你的结论.

分析变式2对例1的特殊结构进行了改变.例1的第3)小题在特殊位置下,得到△ACD是顶角为45°的等腰三角形.改变顶角的度数,使其更加特殊化.当∠CAD=60°时,△ACD为等边三角形.变式2通过线段的数量和位置关系来刻画等边三角形的图形结构.

△GOF∽△BOC,

又

GF=OF,

知

CO=CB.

由于

AB⊥CD,

故

∠BCD=∠OCE.

因为∠BCD=∠BAD,所以

∠OCE=∠BAD,

从而

∠OFA=∠OEC=90°,

于是

CF⊥AD.

因为G为AO的中点,AO为Rt△AFO的斜边,所以

OG=GF,

故

GF=OF=OG,

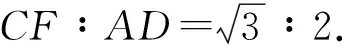
4 思考

4.1 培养作图能力,重视定性分析

作图能力的培养有助于学生几何直观素养的发展[3].教师要培养学生在审题时根据条件进行简单作图的能力.学生能在作图中感受图形形成的过程,形成较为准确的“几何直觉”,不会局限于题目的“死图”,不知其所以然.并且,教师要重视引导学生对图形进行定性分析,对图形元素之间的关系进行联想与合情推理,分析出图形中的“定图”和“动图”,了解“定图”的元素关系、“动图”的变化过程以及引起变化的元素,从而对整个图形结构有宏观的理解.

4.2 积累图形模型,重视定量刻画

积累常见的核心图形模型有助于学生在解决几何问题时能在复杂图形背景下快速洞察关键的图形结构.在日常平面几何教学中,教师要引导学生对常见的核心图形结构进行整理与积累,不只是图形的结构,更重要的是边、角关系和性质的定量刻画以及一般化的代数结论.为了让学生能体会图形结构与定量刻画之间紧密的联系,建议教师在平面几何的新课教学中重视引导学生从多个角度用符号语言去定量刻画同一个图形结构,使学生学会图形语言与符号语言的转化.

4.3 聚焦代数表达,重视建立联系

平面几何的图形结构是对其直观的表达,代数刻画则是对其抽象的表达.构建“图形结构”与“代数表达”的相互关联,有助于获得问题解决的突破口.在平面几何综合问题中,具有挑战的最后一小题,往往是抽象的代数表达.教师要引导学生聚焦其刻画的元素和关系,引导学生从抽象到具象,联想合适的图形结构,添加辅助线进行构造或是还原图形,然后借助几何直观,结合图形性质,再次从具象到抽象,用合适的代数表达,进行推理、证明、运算,从而解决问题.