2023年中考圆与锐角三角函数综合试题的分析与启示
唐亚军, 范明志
(1.南通市海门港新区实验初级中学,江苏 南通 226100;2.阜阳实验中学南校区,安徽 阜阳 236113)
初中学业水平考试(中考)为评价区域和学校教学质量、改进教学提供重要的参考.《义务教育数学课程标准(2022年版)》要求试题命制要“坚持素养立意,凸显育人导向”,既要关注数学的本质,又要关注通性通法[1].圆自古以来就是平面几何的主角,是曲线型图形的代表,无论是与其他几何图形的关系,还是其研究的内容、结构、过程与方法等,都可以给学生更多的自主探究的机会[2],可以更好地培养学生的创新思维、理性思维与科学精神,提升学生的素养.圆是各省市数学中考的必考内容,其中圆与锐角三角函数结合的题目难度大,综合性高,学生总是难以把握这类题型的本质.因此,总结题型,关注此类题的通性通法,是打破该桎梏的重要方法之一.
总结2023年中考圆与锐角三角函数综合试题可以发现,都是进行求值,总体分为3类:“求”三角函数值、“给”三角函数值、“用”三角函数值.
1 “求”三角函数值
该类题型是求某一个角的三角函数值.在初中阶段,三角函数值的计算是放在直角三角形中的,因此,该类题型的本质是作所求角的直角三角形或将所求角转化,找出含有其等角或同角的直角三角形进行解题.
1.1 构造直角三角形法
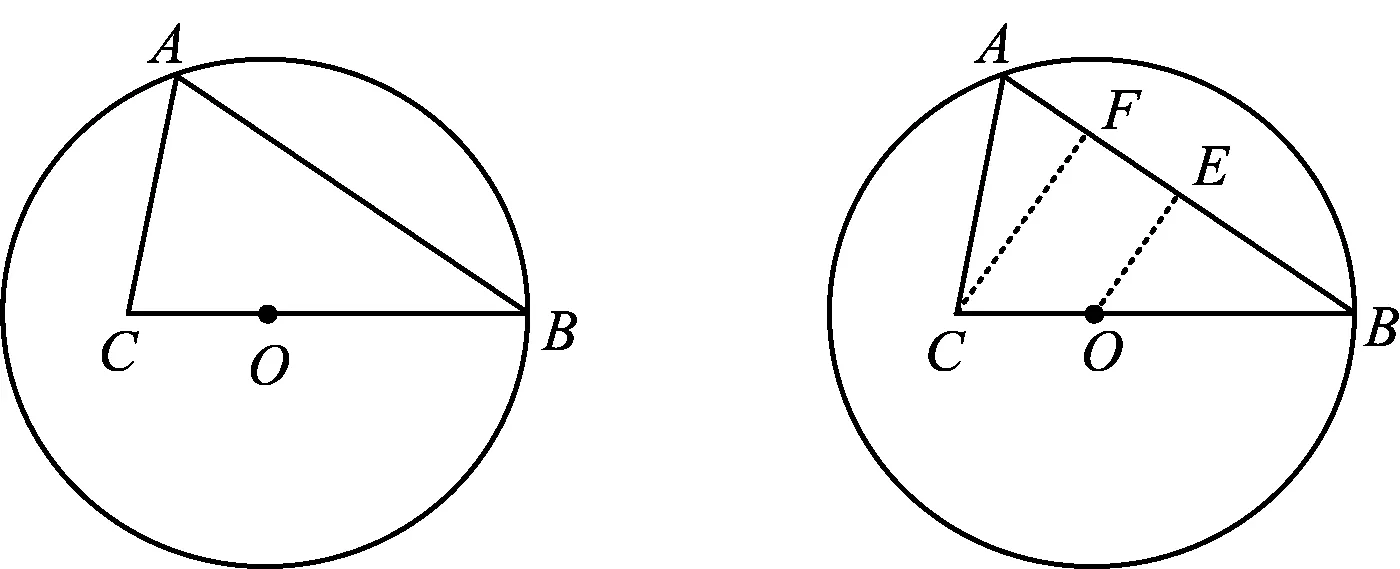
图1 图2
1)求⊙O的半径;
2)求∠BAC的正切值.
(2023年上海市数学中考试题第21题)
分析如图2,作OE⊥AB于点E,CF⊥AB于点F,在第1)小题求出⊙O的半径OB=5之后,相应地求出OE=3,BE=AE=4,OC=2.5.此时要想求出∠BAC的正切值,必须找到含有∠BAC或与∠BAC有等角的直角三角形.观察图2可知图中没有此类型的直角三角形,因此考虑作出含有所求∠BAC的直角三角形.
2)解如图2,过点O作OE⊥AB于点E,过点C作CF⊥AB于点F.因为△BOE∽△BCF,所以
又BO=5,BC=7.5,BE=4,OE=3,则
BF=6,CF=4.5,
从而
AF=2,
故
1.2 等角或同角转化法
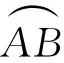

图3 图4
1)求证:AD∥HC;
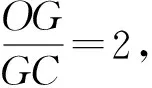
3)略.
(2023年浙江省丽水市数学中考试题第24题)
分析要求tan∠FAG,需找出含有∠FAG的直角三角形,即Rt△AFG,但AF,FG不易求出.由题意可知
∠FAG=∠CAG,
从而
tan∠FAG=tan∠CAG,
利用垂径定理即可求出各边之间的关系.
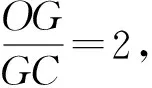
GC=k,OC=OA=3k.
由勾股定理可得
从而
即
2 “给”三角函数值
此类题型是给出某个角的正弦、余弦或正切值,求相关线段的值.这类题往往涉及线段之间的比值关系,进一步结合勾股定理可以表示出这个角或其等角所在直角三角形的三边关系.因此,此类问题的解决方式是:设未知数表示出所求线段和含有已知边长的直角三角形的边长,再利用勾股定理、相似或其他等量关系求解未知数,进而解题.
2.1 构造直角三角形法
例3如图5,AB与⊙O相切于点A,半径OC∥AB,BC与⊙O相交于点D,联结AD.
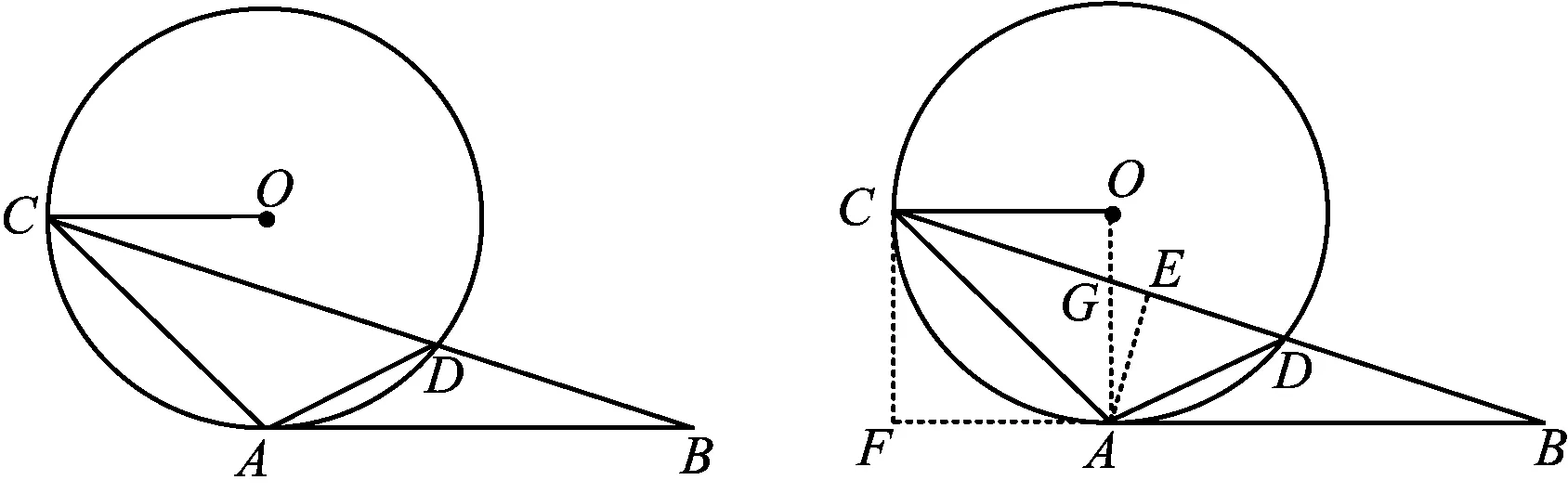
图5 图6
1)求证:∠OCA=∠ADC;
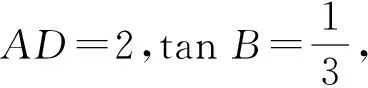
(2023年四川省南充市数学中考试题第22题)


OC=AF=k,BF=3k,
所以
BA=2k.
在Rt△BAE中,
则
在Rt△AED中,
∠ADE=45°,
从而
又因为AD=2,所以
则
即
2.2 参数表示法
例4如图7,AB是⊙O的直径,点C,F是⊙O上的点,且∠CBF=∠BAC,联结AF,过点C作AF的垂线,交AF的延长线于点D,交AB的延长线于点E,过点F作FG⊥AB于点G,交AC于点H.
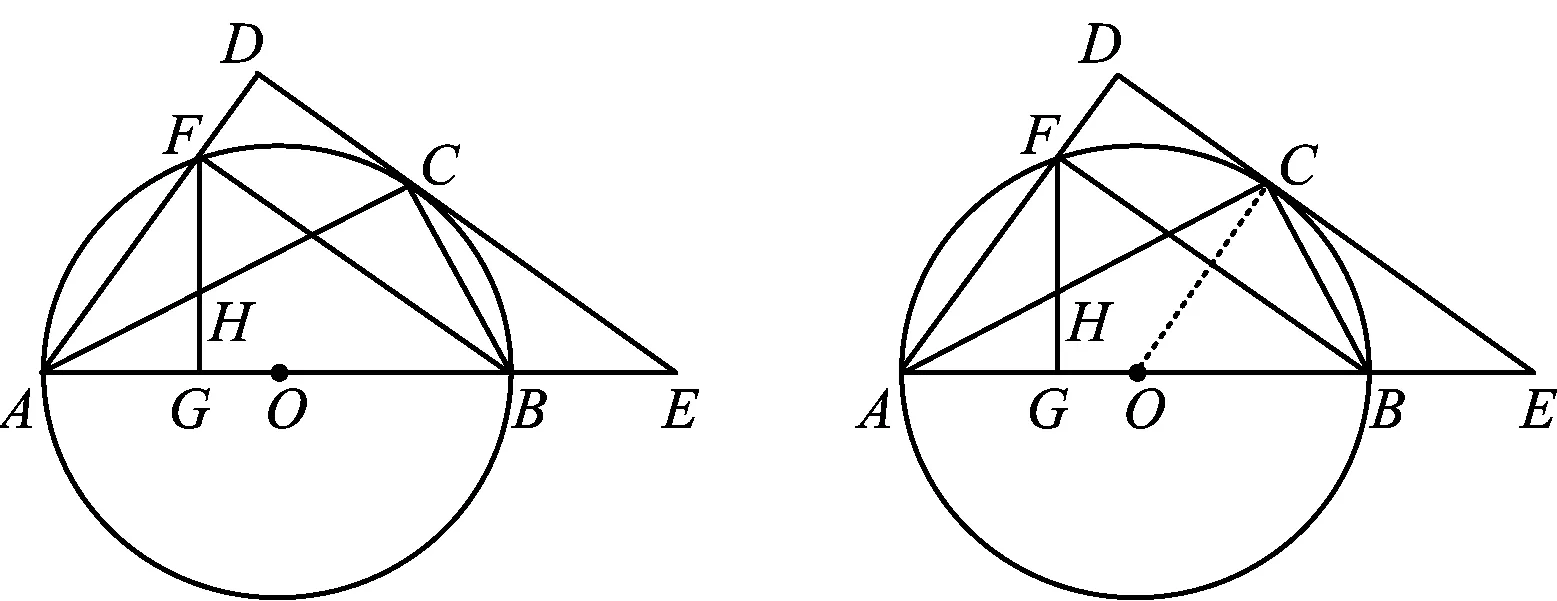
图7 图8
1)求证:CE是⊙O的切线;

(2023年新疆维吾尔自治区数学中考试题第22题)
分析由已知条件可以发现图中有与∠E相等的角,即
∠E=∠ABF=∠AFG.
由于所求FH没有在直角三角形中,因此转化为求FG,HG.若求HG,则可尝试求tan∠HAG的值,从而转化为求tan∠CAD,需要求出DF,CD.

CE=4m,OE=3m+4.
由勾股定理得
m=2,
即
OC=6,CE=8,OE=10,AE=16.
在Rt△EAD中,
设AD=3n,DE=4n,同理可得
则
从而
于是
在Rt△AFG和Rt△BGF中,
设AG=3k,则
从而
得
于是
故
3 “用”三角函数值
“用”三角函数值的实质是在题目中没有给出三角函数条件或让求三角函数值的情况下,给出某个直角三角形的边长或边的关系,使用同角或等角的三角函数快速解题,简化其中较为烦琐的证明步骤.
例5如图9,在△ABC中,以AB为直径的⊙O交BC于点D,DE是⊙O的切线,且DE⊥AC,垂足为点E,延长CA交⊙O于点F.
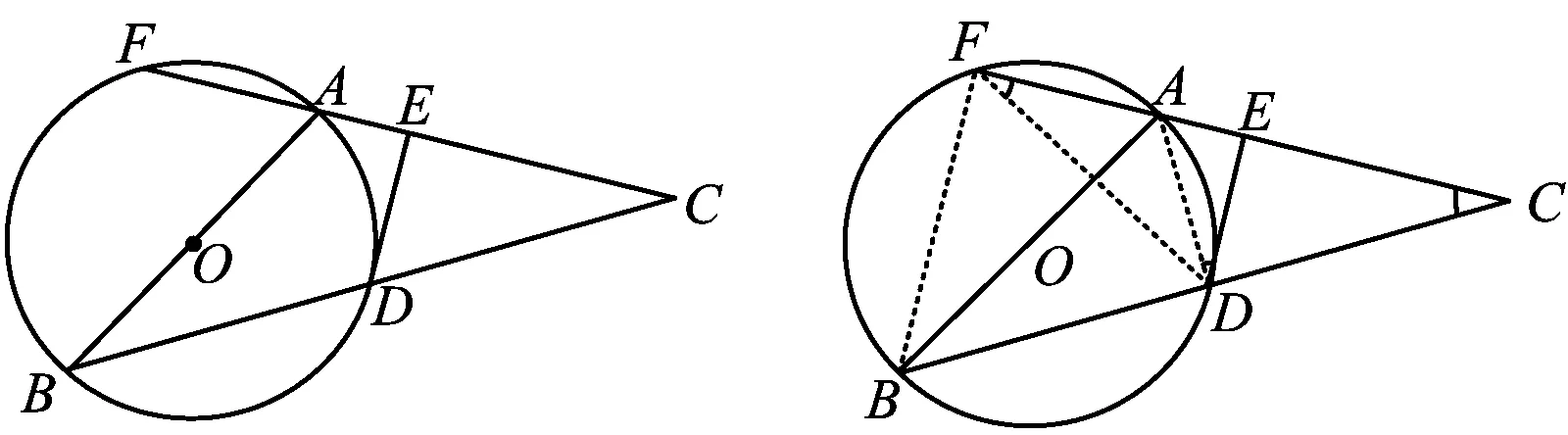
图9 图10
1)求证:AB=AC;
2)若AE=3,DE=6,求AF的长.
(2023年湖北省黄冈市数学中考试题第20题)
分析如图10,由已知条件可知
还可以发现∠DFE=∠ADE,因此只要求出EF的长即可求出AF的长.
2)解如图10,联结AD,BF,FD.在Rt△BCF中,因为D是BC的中点,所以DF=DC,故
∠ADE=∠C=∠DFE.

由
DE=6,
得
EF=12,
从而
AF=9.
结合以上例题,无论是“求”“给”还是“用”锐角三角函数值,其解题过程都涉及线段的长度.究其本质,初中平面几何中的锐角三角函数揭示了直角三角形三边的关系,表达的是三边之间的比例关系.同样表示直角三角形三边关系的勾股定理,其勾股数之间的比例关系即是锐角三角函数,二者之间存在着等价关系.因此,直角三角形就像是“土壤”,而锐角三角函数像是“植物”,锐角三角函数不可脱离直角三角形使用.于是,对于含有任意锐角θ的直角三角形,求出任意两边的值或比例,就可以求出θ的任意三角函数值,继而含锐角θ的任意直角三角形的三边之间的比例关系都可以通过未知数表示出来;已知tanθ,sinθ,cosθ其中一个值,都可以通过设未知数结合勾股数和已知关系表示出其他线段及所求线段.因此,无论题型如何变化,构造“关键直角三角形”,是解决圆与三角函数综合试题最本质的保障.
圆中构造直角三角形的主要方式有作切线、直径所对的圆周角以及利用垂径定理,为锐角三角函数的存在提供基础;同时这3种方式的结合可构造出射影定理(如例4),使得直角三角形中的边角关系联系更加紧密,构造出等角;再者它们都涉及半径,能衍生出很多等角或同角,为角的转化提供了可能性.因此,圆中这3种方式构造的直角三角形往往是“关键直角三角形”,解决问题时要牢牢把握住这些构造方式.

