用联系的观点看解析几何章节起始课的教学
——以“直线的倾斜角与斜率”为例
徐晓芳
(嘉兴市秀州中学,浙江 嘉兴 314033)
平面解析几何是“几何与代数”主线的重要组成内容,是学生感受几何直观与代数运算融合、体悟数学知识之间关联、理解数学整体性的重要载体[1].“直线的倾斜角与斜率”是解析几何的章节起始课,是学生运用坐标法按照解析几何的“基本套路”解决问题的首次实践.本节课渗透了解析几何的思想方法,帮助学生初步了解几何要素代数化的过程,为整个解析几何的后续学习奠定了认知基础.那么,如何在联系的观点启发下,发现学习内容与已有经验、知识、思想方法与文化的多角度、多层次联系?如何让章节起始课更好地体现知识的整体性、逻辑的连贯性、方法的普适性、思想的一致性?本文以人教A版《普通高中教科书·数学》(以下统称“教材”)中“直线的倾斜角与斜率”为例来谈谈看法.
1 联系的3个层次
1.1 教学生成的基石:知识与经验的联结
1.2 数学思维之道:思想与方法的联结
在本节课之前,学生已经知道三角函数通过坐标法将任意角α与其终边和单位圆交点P的坐标建立起函数关系,又通过坐标法将圆的旋转对称性转化成了三角恒等变换公式,向量更是利用坐标法将图形中的几何性质转化为向量的坐标运算.在本节课中,学生将学习先观察直线的几何特征,建立坐标系,然后将图形的几何性质转化为代数形式,通过代数运算研究几何问题.通过前后知识对比,学生发现新问题的解决模式与之前三角函数概念的引入、向量的坐标化完全一致,后续学习圆、椭圆、双曲线、抛物线又加深了这种印象,即解析几何的问题解决模式是“几何图形—建立坐标—几何性质代数化”.在这些“完全一致”之间,学生浸润式地学习与体会了“怎样去研究数学”,即数学“思维之道”.
1.3 数学文化性的体现:理性精神的一以贯之
在本节课中,推导斜率计算公式本质上是坐标法下的一次数形转化.我们已经知道数形结合思想与坐标法在解决平面几何问题中具有强大的普适性,即可以用一种程序性方法解决一众纷繁复杂的几何问题,且将研究由定性推向定量.这也是近代哲学之父笛卡儿创立解析几何的初衷之一.笛卡儿深受数学理性思维与数学研究方式的影响,折服于数学简洁、抽象、统一的美和超越感官与表象对事物本质从理性角度无限穷究的精神[2].而这些无疑是隐藏在解析几何与其他数学内容背后的深度文化联结.教师要引领学生感悟,以冲破具体知识的束缚在更广、更高的文化维度上俯瞰知识,体验数学哲思,感悟数学与世界、自我的联系.
2 联系观点下解析几何教学的案例展示
2.1 整体规划,构建联系方法主线
问题1通过章导言的学习,请简单评价一下综合法与坐标法.
问题2坐标法在以前用过吗?最早一次在哪里?
问题2-1三角函数如何定义?
问题2-2类比三角函数、向量、复数、立体几何等内容,如何对直线开展研究?
问题3用坐标法研究直线时,若把一条直线“放到”坐标系里面去,则可以有几类放法?
问题3-1直线的倾斜程度是有差异的,如何刻画这种差异?

2.2 设核心问题,铸联系之锚
问题4依据直线的4类倾斜情况,若在直线l1上任取一点P(x,y),根据以往经验猜测,横坐标x与纵坐标y的关系如何?
问题4-1倾斜角0°,90°对应的直线,其横坐标或纵坐标有何特征?
问题4-2对倾斜角更为一般的情况,你能找到x与y的关系式吗?
评注问题4是核心问题,它既联系了初中旧知,又挖掘了函数与方程的内在关系,同时渗透了坐标法求解曲线方程的关键思路,为本节课及后续直线方程、圆锥曲线等研究指明了方向,是立足本课放眼全章的联系之锚.
2.3 于多对联系中,形成猜想
问题5如何确定y=kx+b中k,b的值?
问题5-1确定一条直线的几何要素是什么?
问题6求解问题,并尝试推测k值与直线上两点坐标、直线方向向量的可能关系:
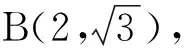
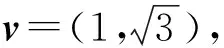
问题6-1两个问题有没有关系?
问题6-2你有什么猜想吗?可以证明吗?

2.4 在数形转化中,强化知识本质,构建整体联系
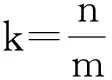

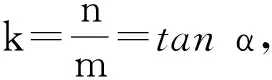

问题7-4你能说说斜率k与一次函数y=kx+b中常数k的联系吗?对于初中一次函数图象“当k>0时,直线从左向右上升;当k<0时,直线从左向右下降”,你能用今天的知识解释吗?
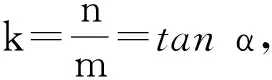
2.5 一题多解,多法联结
问题8若直线l1经过点P1(x1,y1)和P2(x2,y2),其中x1≠x2,则斜率如何求?
评注鼓励学生从多个角度分析问题,获得多种解法,以实现对斜率更全面地理解.
2.6 比较、延展,纵横联系
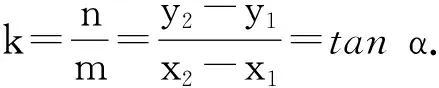
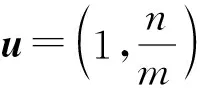

评注问题9与问题9-1在延展中强化了斜率与向量特别是方向向量的纵向联系;问题9-2在同一对象不同表述的比较中,加强斜率多个表达形式的横向联系.
2.7 首尾呼应,由本节辐射全章
问题10本节课伊始,已经简单评价过综合法与坐标法,那么通过倾斜角与斜率的学习,大家对此有新的认识吗?
问题11我们已经通过坐标法把直线的倾斜程度这个“形”的东西转化为“数”的形式.那么,如何把直线由“形”转化为“数”呢?
评注问题10引导学生由对具体知识的关注回归到获得知识的数学思想方法——坐标法与数形结合上来;问题11继续引导学生反思斜率的获得过程.由于问题4的铺垫以及对初中一次函数知识等的回顾,学生已经初步探明直线上任意一点横坐标与纵坐标的关系,为后面直线方程的学习埋下伏笔.
2.8 多样作业,文化引领
作业1习题2.1复习巩固1~4,教材第55页练习4和练习5.
作业2了解笛卡儿的生平与其生活的17世纪的文化背景,评论数学的研究方法对17世纪文化、科学、艺术等多领域的影响.
3 联系观点下解析几何章节起始课教学的思考
由于在联系中下足了功夫,整节课兼顾了知识的整体性、逻辑的连贯性、方法的普适性、思想的一致性,在学生中收到了良好的反馈.总结起来,联系观点下解析几何章节起始课的教学需要在以下几个方面做出切实努力.
3.1 需要充分调动学生的已有知识和经验

3.2 必须有本质的核心问题的提出
斜率的本质是直线倾斜程度的代数表示,而实现数与形转化的方法就是坐标法.如何让学生自然地想到坐标法并且深入领会数形结合思想?核心问题的设置显得特别重要.本节课通过设置问题2,4,5,7,11等,特别是通过问题4与问题11,使得从坐标法的引入到对直线上任意一点横坐标与纵坐标关系的探讨,再到数学思想方法的回归,整节课首尾呼应、浑然一体,不仅将一次函数、倾斜角、方向向量、三角函数、斜率等一众概念内置于问题4的探索过程中,创新了倾斜角与斜率的引入方式,还凸显了解析几何处理问题的一般方法以及背后的数学思想.又比如斜率公式的探究是一个综合运用知识的过程,有的方法对部分学生而言有难度,如何铺垫使其自然生成?问题2-1让铺垫顺其自然,问题8则为学生创造了一个综合运用知识、多角度理解斜率概念的机会.
3.3 必须要有一般观念的指导与文化精神上的引领
圆、椭圆、双曲线、抛物线的研究都是从图形的几何要素(定义)开始,再通过它们的代数方程探究,如几何性质、位置关系等问题.而直线却是从斜率、位置关系再到方程,与解析几何总体的研究路径不一致.本节课通过“整体规划,构建联系方法主线”与“设核心问题,铸联系之锚”两个部分,将探求曲线方程的关键方法——寻得曲线上任意一点的横坐标与纵坐标的关系渗透进教学.这样做,一来使得整个解析几何的研究路径更为连贯一致;二来为后续直线方程的学习埋下伏笔;三来使得本节课在坐标法与数形结合等重要解析思想的运用上有了两条线——一条线是倾斜程度与斜率的数形转化;另一条线是直线与直线方程的数形转化.此外,本节课通过设置作业2,给学生创造了冲破具体知识的束缚在更广、更高的文化维度上俯瞰知识、体验数学文化哲思、感悟数学理性精神的机会.

