让几何直观自然生长

徐亚飞

［摘  要］ 几何直观主要是指运用图表描述和分析问题的意识与习惯.能够感知各种几何图形及其组成元素，依据图形的特征进行分类；根据语言描述画出相应的图形，分析图形的性质；建立形与数的联系，构建数学问题的直观模型；利用图形分析实际情境与数学问题，探索解决问题的思路.

［关键词］ 圆周角；几何直观；猜想；验证

“几何直观”是《义务教育数学课程标准（2022年版）》提出的核心素养主要表现之一，几何直观主要是指运用图表描述和分析问题的意识与习惯. 能够感知各种几何图形及其组成元素，依据图形的特征进行分类；根据语言描述画出相应的图形，分析图形的性质；建立形与数的联系，构建数学问题的直观模型；利用图形分析实际情境与数学问题，探索解决问题的思路. 几何直观有助于学习者把握问题的本质，明晰思维的路径.

活动一：情境引入，发现新知

课前播放足球射门的精彩瞬间的视频.

思考：如图1，在足球比赛场上，甲、乙两名队员互相配合向对方球门MN进攻，当甲带球冲到A点时，乙已跟随冲到B点. 从射门角度看，此时甲是自己射门好，还是将球传给乙，让乙射门好？

设计说明  踢足球是学生比较喜欢的一项体育运动，从学生喜爱的足球引入新课，激发了学生学习数学的热情，调动了学生学习数学的积极性. 通过欣赏足球射门的视频，学生感受到数学与自己的生活息息相关、不可分割，同时也感受到数学的魅力无处不在.

活动二：复习回顾，引入新知

复习回顾圆心角的定义（顶点在圆心的角叫作圆心角）及其性质（圆心角的度数等于其所对弧的度数）.

思考1：改变圆心角的顶点P的位置，这个点P除了在圆心，还可以在哪些位置呢？（圆内、圆上、圆外）

思考2：尝试给这三个角命名. （圆内角、圆周角、圆外角）

由此引出今天的课题“圆周角”.

设计说明  复习回顾圆心角的定义和性质，通过改变圆心角顶点P的位置，自然而然地引入了圆内角、圆周角以及圆外角，让学生感受到数学知识前后的连续性.

活动三：类比学习，探究新知

（一）圆周角的概念

思考1：类比圆心角的学习，圆周角将从哪些方面来学习？（定义、性质等）

思考2：对于顶点在圆周上的角，改变角的两边与圆的位置关系（如图2、图3），得到另两类顶点在圆周上的角，判断这两类角是否是圆周角.（不是）

思考3：根据黑板上的图形以及你对圆周角的理解，尝试给出圆周角的概念（顶点在圆周上，两边与圆相交的角）

判断：如图4，∠P是圆周角吗？（是，角的两边是射线）

思考4：回忆圆心角的定义（顶点在圆心的角），为什么圆心角的定义只要满足一个条件，而圆周角的定义却要满足两个条件？

设计说明  根据圆周角的图形，让学生自行归纳出圆周角的定义，培养学生的语言表达能力和自主学习的能力. 区别圆心角和圆周角定义的不同，加深学生对概念的理解.

练习：如图5，弧CD所对的圆周角是______；

∠ACB所对的弧是______；

弦BD所对的圆周角是______.

设计意图  通过这道题目，让学生感受一条弧所对的圆周角不止一个，但一条弧所对的圆心角却只有一个，进而引导学生发现一条弦所对的圆周角也有无数个，且可以分为两类.

设计说明  通过类比圆心角的学习过程来探究圆周角的学习过程，培养学生自主学习的能力. 圆周角的概念比圆心角的概念多了一个条件“角的两边与圆相交”，通过一组题目让学生感受为什么要加上这样一个限制条件，以加深学生对圆周角概念的理解.

（二）圆周角的性质

猜想1：同弧所对的圆周角相等.

实验验证1：几何画板验证“同弧所对的圆周角相等”.

通过几何画板的演示，我们发现同弧所对的圆周角相等.

思考：同弧所对的圆周角为什么会相等？（相等的圆周角所对的弧是同一条弧）

设计意图  通过画图、度量、猜想、几何画板验证，让学生初步感知“同弧（等弧）所对的圆周角相等”，通过改变弧的长度，让学生再次感受圆周角的大小与其所对的弧有着密切的联系.

猜想2：同弧所对的圆周角的度數是圆心角度数的一半.

实验验证2：几何画板验证“同弧（等弧）所对的圆周角的度数是圆心角度数的一半”.

设计意图  通过画图、度量、猜想、几何画板验证，让学生初步感知“同弧（等弧）所对的圆周角的度数是圆心角度数的一半”.

对于这两个猜想，我们用几何画板进行了验证. 当然，要说明这两个猜想是正确的，必须要给出数学证明.

我们先来证明第二个猜想：同弧所对的圆周角的度数是圆心角度数的一半.

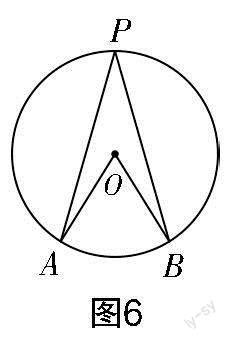
教师展示如图6所示的图形（来源于学生）：

思考1：大家所画的圆周角和圆心角的位置关系和这幅图一样吗？

投影仪展示学生的不同画法（如图7、图8）.

思考2：三幅图的不同点在哪里？（圆周角和圆心角的位置不同）.

思考3：大家想先证明哪一幅图？

我们在研究一类图形的时候，常常是从特殊到一般. 图7最为简单，用外角即可解决. 图6、图8均可通过添加适当的辅助线转化为图7来解决，也就是我们常说的把未知的知识转化成已有的知识来解决，当然，我们也可以用已有的知识去探究未知的知识.

设计说明  让学生经历动手操作、观察、猜想、实验、推理等过程，一步步地来探究圆周角的性质，培养学生独立分析问题、解决问题的能力. 两个猜想，到底先证明哪一个呢？其实只要证明了“同弧所对的圆周角的度数是圆心角度数的一半”，就能得到“同弧（等弧）所对的圆周角相等”. 对于“同弧所对的圆周角的度数是圆心角度数的一半”的证明，又要分三种情况来讨论，这也是本节课的一个难点：①为什么要分类？②分类依据是什么？③三种情况又分别如何证明？教师层层引导，激发学生的思维活力.

活动四：课堂小练，巩固新知

思考：在同圆或等圆中，同弧所对的圆内角、圆周角、圆外角之间的大小关系如何？（如图12）

在同圆或等圆中，同弧所对的圆内角>圆周角>圆外角.

设计说明  通过一组题目的训练，既夯实了本节课的两个重要的知识点，又为接下来引出圆周角、圆外角以及圆内角之间的大小关系做好铺垫，更为接下来解决“情境引入环节”遗留的“足球问题”埋下伏笔.

活动五：情境再现，学以致用

思考：如图13，在足球比赛场上，甲、乙两名队员互相配合向对方球门MN进攻，当甲带球冲到A点时，乙已跟随冲到B点. 从射门角度看，此时甲是自己射门好，还是将球传给乙，让乙射门好？

设计说明  再次回到课前的情境引入，不难发现之前的难题已经迎刃而解. 让学生意识到学习数学就是为了解决生活中所遇到的一些问题，由此激发学生学习数学的积极性.

活动六：课堂小结，提升新知

（1）圆周角有何特征？与圆心角有何异同点？（2）在证明圆周角定理时，你积累了哪些重要的方法？（3）你还有哪些疑惑？

设计说明  通过一组问题串，进行有针对性的课堂小结，帮助学生梳理本节课的知识要点，构建本节课的知识框架，提升本节课的思想方法，培养学生的自主学习能力，提升学生良好的学习品质.

教学反思

本节课设计了三个环节：第一个环节是圆周角概念的得出. 从学生熟悉的足球射门入手，并埋下伏笔，激发学生学习新知的欲望，提高学生学习数学的积极性，同时也让学生感受到生活中处处都有数学. 通过复习圆心角的概念和性质，帮助学生回忆圆心角的学习过程，进而引导学生发现：圆周角的学习可以类比圆心角的学习过程来进行. 第二个环节是探究圆周角定理. 通过学生的动手操作：先画再度量，最后猜想并验证，让学生经历动手操作、思考探究、归纳猜想、理论证明等一系列学习过程，培养学生的综合能力. 在证明“圆周角的度数等于它所对弧的圆心角度数的一半”这个定理时，没有直接给出三种类型，而是让学生在自我实践中发现：这个图形有多种可能性，必须分类讨论，从而培养学生分析问题和解决问题的能力. 第三个环节就是学以致用. 用今天所学的内容来解决与圆周角有关的问题，从而解决了课前情境引入中的足球射门的问题，让学生感受到数学来源于生活，又服务于生活！

借助几何直观，通过自主探索、发现和再创造，让学生体验数学创造性的学习历程，激发学生的创造热情，使学生形成良好的思维品质. 弗赖登塔尔曾说過：“几何直观能告诉我们什么是可能重要、可能有意义和可接近的. ”运用几何直观，学生的思维便有了一定的载体，不再空洞乏味，由此加深学生对知识的理解，激发学生对数学学习的热情，从而迈向数学学习的最终目标：让学习者学会用数学的眼光观察现实世界，学会用数学的思维思考现实世界，学会用数学的语言表达现实世界.