探索一类与圆锥曲线焦点弦有关的定值问题

山东省宁阳县复圣中学 (271400) 张志刚

1 案例呈现

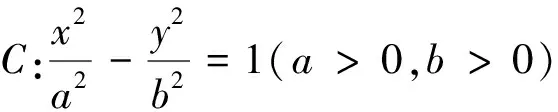
(1) 求双曲线C的方程;

(2) 过双曲线C的右焦点作直线l(与x轴不垂直)与曲线C交于M,N两点,线段MN的垂直平分线交x轴于点P,是否存在实常数λ,使得|MN|=λ|PB|?若存在,求出λ的值;若不存在,请说明理由.

本题考查双曲线的标准方程、直线与双曲线的位置关系等内容,突出考查学生的数学运算、数学抽象、逻辑推理等核心素养,以及综合应用所学知识分析问题和解决问题的能力.试题立意高远深邃,构思别出心裁,结构清晰明朗,解法活泼灵动,充分体现了多层次、高落差的素养导向,堪称一道有丰富内涵和推广价值的经典试题.

2 案例解答

思路一 利用通用的弦长公式表示弦长

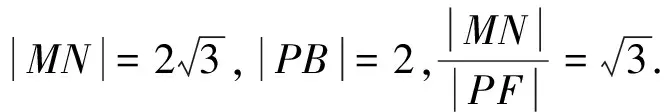
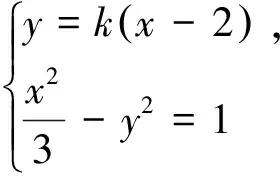
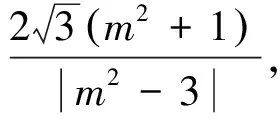
思路二 利用双曲线焦点弦|MN|=|e(x1+x2)-2a|表示弦长

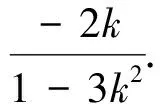
解法4：(点差法、选斜率k为参数)由题意设

解法6：当M,N两点位于双曲线同一支时,不妨设M,N位于双曲线右支上,设双曲线的右焦点B(3,0)到右准线的距离为p,MN与x轴的夹角为θ(0<θ<π).

3 问题推广

本结论证明方法较多,例如上述解法6,下面再类比解法2(反设直线)给出证明.

类比双曲线,椭圆和抛物线有同样结论.

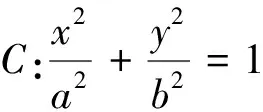
将命题进一步推广即有结论4.

本结论揭示了圆锥曲线的焦点弦、焦点弦的中垂线与坐标轴交点二者之间的紧密联系,得到了与焦点弦长有关的一个定值结论.

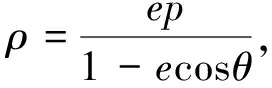
4 应用举例

(1)求椭圆W的方程;

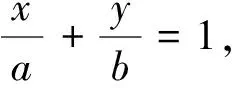
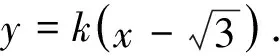
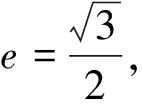
例2 (2022年10月全国C8名校协作体联考第21题)已知圆A:x2+y2+6x+5=0,直线l(与x轴不重合)过点B(3,0)交圆A于C,D两点,过点B作直线AC的平行线交直线DA于点E.

(1) 证明:||EB|-|EA||为定值,并求点E的轨迹方程;

(2) 设E点的轨迹为C1,直线l与曲线C1交于M,N两点,线段MN的垂直平分线交x轴于点P,是否存在实常数λ,使得|MN|=λ|PB|?若存在,求出λ的值;若不存在,请说明理由.

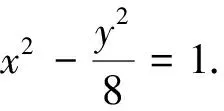
“以问题为载体,以知识为基础,以思维为主线,以能力为目标,全面考查学生的学习潜能”仍然是当前高考命题的一个重要方向.在学习中我们要充分挖掘试题所蕴含的丰富教学资源,以试题研究为主阵地,利用问题的相似性和知识的系统性,我们可以把与此相关的问题进行归纳推理,以期对其一网打尽.