从直观想象到思辨论证编制与解答试题*——以2019年高考全国Ⅱ卷理科第22题为例

福建省泉州第一中学 (362000) 黄寒凝

福建省泉州第五中学 (362000) 杨苍洲

观察函数的图象特征,通过直观感知,可以从中提出各种问题,为试题编制提供问题情景.然而,由于观察误差等,直观感知所得的结论,并不一定都是正确的,这就需要通过演绎推理进行操作确认.因此,试题的命制常常是通过“直观感知”提出问题,再通过“思辨论证”保障所提问题的科学性.

一、直观想象——在图象中提出问题

对数函数f1(x)=lnx和指数函数f2(x)=ex是高中阶段重要的两个基本初等函数.f1(x)与f2(x)互为反函数,它们的图象关于y=x对称;f1(x)在(0,+∞)单调递增,f2(x)在R上单调递增;f1(x)在(0,+∞)上凸,f2(x)在R上下凸.从函数的图象趋势可以观察得f1(x)与f2(x)的图象有两条公切线,且两条公切线也关于y=x对称.如图1所示.由此,可提问题1.

图1

问题1 证明:曲线f1(x)=lnx与曲线f2(x)=ex有两条公切线.

既然f1(x)与f2(x)的图象有两条公切线,那么,我们试着探究一下切点的位置.顺着问题1的思路,可提出问题2.

问题2 曲线f1(x)=lnx在点A(x0,lnx0)处的切线与f2(x)=ex也相切.若x0∈[n,n+1)(n∈Z),求n的值.

“逆向思维”往往是提出一个新问题的捷径.结合问题2探究过程及结论,逆向改编,可以提出问题3.

这就是2019年高考全国Ⅱ卷理科第22题的命题思路,试题附录如下:

二、思辨论证——在推理中寻找答案

如何证明或求解上述三个问题呢?

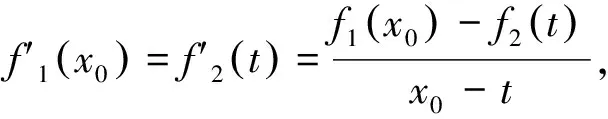
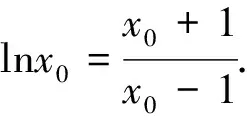
三、结语

直观想象是发现问题和提出问题,分析问题和解决数学问题的重要手段,是探索和形成论证思路、进行逻辑推理、构建抽象结构的思维基础.试题的编制与解答常常是从直观想象到思辨论证的过程,运用直观想象有助于数学的解题与命题.