2022年高中数学联赛A2卷平面几何题的另解

华中师范大学第一附属中学 (430223) 陈开懋

受疫情影响,2022年全国中学生数学奥林匹克竞赛(预赛)暨2022年全国高中数学联合竞赛,湖北和山东延期了两次,于11月27日顺利组织了考试.此次考试用的是A2卷,加试的平面几何题放在了第二题的位置,增加了难度,除了答案提供的两种解法外,本文再给出两种解法.

图1

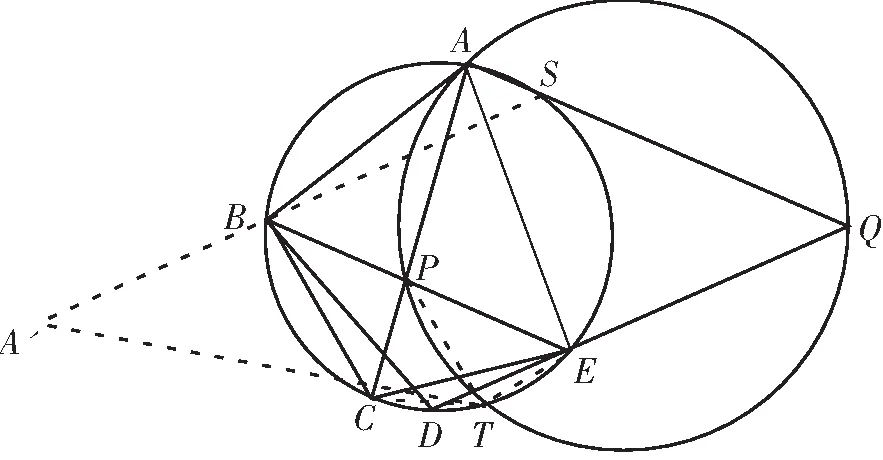
图2

∠AEC,又A′与A关于BC对称,所以∠A′BC+∠SBC=∠ABC+∠AEC=180°,故A′,B,S三点共线.

评析：证法一主要是分为三个步骤,第一步,证明A′,B,S三点共线,第二步,证明A′,P,Q三点共线,第一步,证明∠BA′P=∠BTP,从而A′,B,P,T四点共圆.该证法主要是优化了第二步.

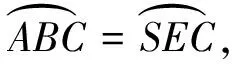
图3

评析：证法二主要分了两个步骤,第一步,同证法一,证明A′,B,S三点共线,第二步,证明ΔTA′S∽ΔTPE,主要采取了三角计算的方法,要求三角恒等变换比较扎实.

这两种解法是比较初等的方法,证法二主要采取了三角计算,比证法一繁琐复杂,当然本题还可以用更高级的几何定理(帕斯卡定理)来证明,有兴趣的同学和老师可以自己去尝试.