一道直线与椭圆试题的解法探究与变式

江苏省海门中学 (226100) 姜敏华

直线与圆锥曲线的综合问题在考试中一直处于压轴题的位置,对于学生而言,难点主要体现在两点:一是思路不清晰,二是计算能力不足.因此在解题教学中要帮助学生分析条件找寻思路,带领学生看清本质,突破运算难点.本文以一道直线与椭圆试题为例谈谈如何帮助学生寻找思路,突破运算难点,同时充分挖掘试题展开变式探究.

一、题目

本题第(2)问将条件隐藏于三角形面积和边长之间的等量关系之间,考查学生转化与化归的能力.题目中字母多,变量多,难点在于如何建立k与k′之间的关系式.

二、解法剖析

因此sin∠APQ=sin∠BPQ,而∠APQ+∠BPQ=∠ABP∈(0,π),有∠APQ=∠BPQ,于是PQ平分∠APB,直线AP,BP的斜率kAP,kBP互为相反数,即kAP+kBP=0.

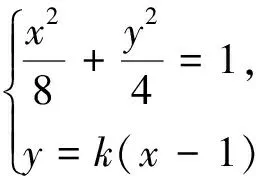
解法二：设A(x1,y1),B(x2,y2),P(x0,y0),直线AP:y=k0(x-x0)+y0,联立

评注：此方法,变换思路由点P出发,引两条斜率互为相反数的直线与椭圆交于A,B两点,求出点A,B的坐标,计算kAB即可找到问题的解,同时运算量也大大减少,只需求点A坐标,点B坐标同理可得.但是学生很有可能会利用A,B和点(1,0)三点共线处理,此时偏离了目标,同时根据此方法还可以发现kk′为定值与直线l是否过点(1,0)无关.

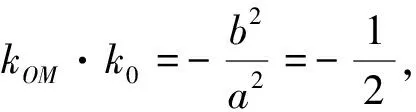
评注：该方法联想到了椭圆弦中点的结论,将AB的斜率转化为中位线MN的斜率,从而只需求出PA,PB的中点M,N即可,利用结论转化为两条直线的交点,从而简化了问题的运算量.

评注：该方法在法三的基础上,对PA,PB的斜率从两个不同的方向寻找等量关系,从而建立起点P与AB中点与原点O斜率之间的等量关系,从而利用中点弦的结论将问题解决.运算量少,但对学生的思维能力要求较高.

评注：看到kAP+kBP联想到一元二次方程的两根之和,从整体上构造关于AP,BP斜率的一元二次方程,将直线与椭圆联立齐次化建立方程,从而解决问题.问题的难点在于对方程的变形构造.

上述五种解法中方法二的过程最简单直接,可操作性强,也需要学生能够灵活的变换点线之间的关系.

三、变式探究

思考1 由解法二发现kk′为定值与直线l是否过定点(1,0)无关,因此,可以得到更一般的结论.

思考2 采用逆向思维,考虑原问题的逆命题是否成立?

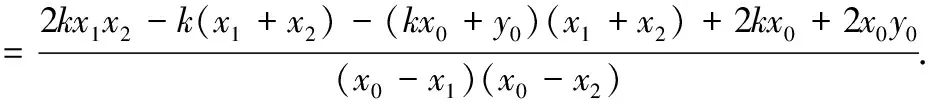
上述变式均可以类比到双曲线中,限于篇幅,不在赘述.一道好题,不仅可以查学生的能力,提升学生的学生的运算能力和思维水平,同时还能够给学生创造探究的机会,给学生积累数学探究的经验.对好题从不同的角度思考融合,可以变化出很多优美的题目.