解几问题中找不等关系求范围的几点探索

山东省沂南县第二中学 (276300) 赵 亮

在解析几何问题中,有关不等关系的探究也是十分重要的,它是解决参数或相关元素取值范围的关键举措.部分学生找不到不等式,或是建立的不等式不合理,往往造成解题错误,使待求的问题不能得到圆满解决.为此,本文通过举例分析,介绍寻找不等关系求有关范围问题的六种方法,希望能给读者朋友有所帮助.

一、抓住已知的不等关系

有的题目的题设中,已经给出了一些不等的关系,在解决有关范围问题时,应该首先考虑此条件的充分运用.

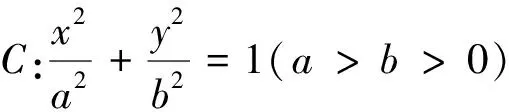
评注：由于题中给出了离心率的范围,这是一个重要的不等关系,所以整个解题都必须围绕如何建立λ与a,b,c来操作,其中运用向量相等的条件起关键作用.

二、利用点与曲线的位置关系

题设中的给出的某些特殊点与已知曲线的关系必须得到关注,它是可能存在隐含着的不等关系的,解题中也是建立不等式重要依据.

例2 设A(x1,y1)、B(x2,y2)两点在抛物线y=2x2上,l是AB的垂直平分线,当直线l的斜率为2时,求l在y轴上截距离的求值范围.

评注：从题目的条件中没有不等关系的存在,但段线AB的垂直平分线是特殊的直线,对此深挖研究,即可得段线AB的中点在抛物线内部的隐含条件,于是获得了需要的不等式.

三、依据圆锥曲线的几何特征

圆锥曲线的本身也隐含着许多不等关系,如焦点三角形、曲线上的点与准线的关系等,这些特殊位置的条件,必要时也必须予以考虑.

评注：圆锥曲线也是一类特殊曲线,它们的几何特征非常明显,解题中需要注意这些特性的限制,从中探究出不等关系非常必要,如本题中的焦点三角形三边的不等关系的运用.

四、关注相关动点的限制条件

在有些题目中,某些动点的变化应符合一定的条件,如在某个线段上、某个圆上,解题时也应该注意其中条件的制约.

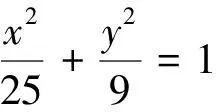
评注：本题中的动点M在线段CD上,所以有限制条件,解题中应该充分关注到.同样,如果已知动点在某一个已知曲线上,也需要注意到曲线的范围对此点的限制.

五、挖掘代数变形中隐含条件

在有关式子的运算变形中也包含着不等关系,如满足正数解的条件、通过配方得到的完全平方式等,这其中也是解决范围问题的客观条件.

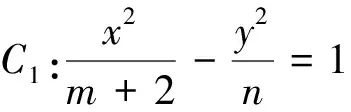
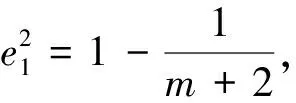
六、从直线与曲线相交情况中去判断

直线与曲线相交是特定的位置关系,对应于相应的方程来说,就是二次方程根的判别式,这是建立不等式的重要条件,应予以重点考虑.

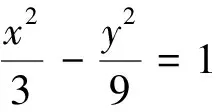
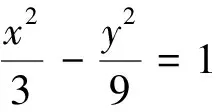
评注：直线与双曲线相交于两点是重要的几何条件,而它的代数特征则就表现为△>0,利用这个知识点可解决许多参数范围问题,反之利用△,也可判断直线与曲线的位置关系.

以上的举例是探求解析几何问题中不等关系,求参数范围的常用方法,其解题关键就是善于挖掘问题中所存在的不等关系,在解题教学中,我们应该引导和帮助学生探寻解题规律、研究解题方法、归纳常用的解题思路,这样就可以使课堂教学收到更好的成果.